الفرق بين قيم z وقيم p في الإحصائيات

المصطلحان اللذان غالبًا ما يخلطهما الطلاب في الإحصاء هما قيم z وقيم p .

لفهم الفرق بين هذه المصطلحات، من المفيد فهم اختبارات z .

هناك نوعان شائعان من اختبارات z:

• اختبار z لعينة واحدة : يستخدم لاختبار ما إذا كان متوسط السكان يساوي قيمة معينة.
• اختبار z لعينتين : يستخدم لاختبار ما إذا كان متوسطان سكانيان متساويان.

نستخدم الخطوات التالية لإجراء كل اختبار:

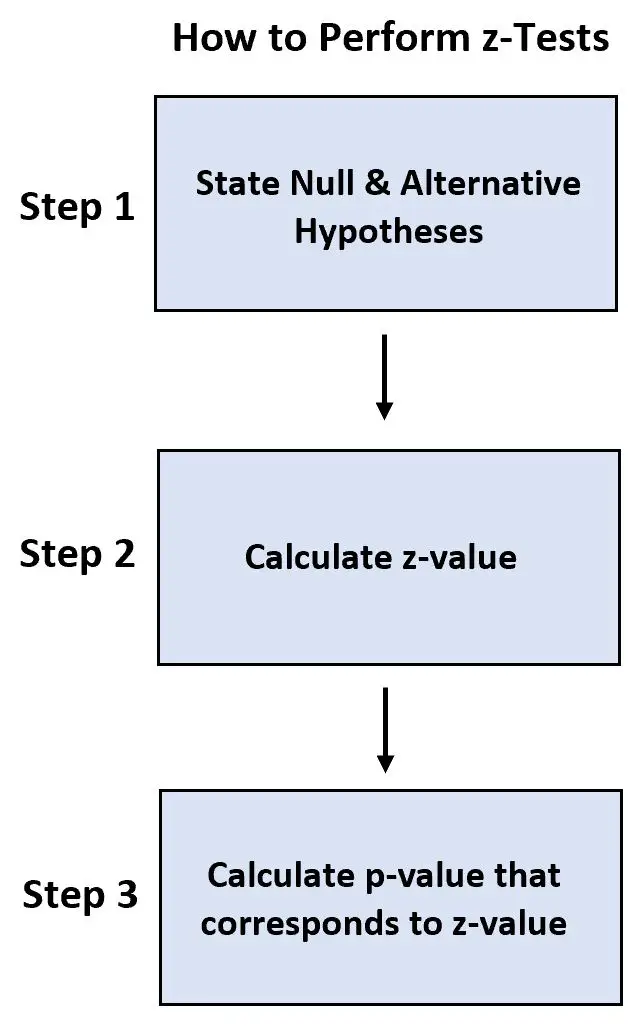
• الخطوة الأولى: اذكر الفرضية الصفرية والبديلة.
• الخطوة 2: احسب قيمة z.
• الخطوة 3: احسب القيمة p التي تتوافق مع القيمة z.

بالنسبة لكل اختبار، تعد قيمة z وسيلة لقياس الفرق بين متوسطات السكان والقيمة p هي احتمال الحصول على قيمة z بقيمة مطلقة كبيرة على الأقل كما لاحظنا بالفعل في “العينة”. البيانات إذا كانت الفرضية الصفرية صحيحة بالفعل.

إذا كانت القيمة p أقل من قيمة معينة (على سبيل المثال 0.05)، فإننا نرفض الفرضية الصفرية للاختبار.

لكل نوع من اختبارات z، نحن مهتمون بالقيمة p ونستخدم ببساطة القيمة z كخطوة وسيطة لحساب القيمة p.

يوضح المثال التالي كيفية حساب وتفسير قيمة z وقيمة p المقابلة لاختبار z المكون من عينتين.

مثال: حساب وتفسير قيم Z وقيم P

افترض أن مستويات الذكاء للأفراد من مدينتين مختلفتين يتم توزيعها بشكل طبيعي، ولكل منها انحرافات معيارية سكانية تبلغ 15.

يريد أحد العلماء معرفة ما إذا كان متوسط مستوى الذكاء بين الأفراد في المدينة (أ) والمدينة (ب) مختلفًا. ولذلك قامت باختيار عينة عشوائية بسيطة مكونة من 20 فردًا من كل مدينة وسجلت مستويات الذكاء لديهم:

المدينة أ : 82، 84، 85، 89، 91، 91، 92، 94، 99، 99، 105، 109، 109، 109، 110، 112، 112، 113، 114، 114

المدينة ب : 90، 91، 91، 91، 95، 95، 99، 99، 108، 109، 109، 114، 115، 116، 117، 117، 128، 129، 130، 133

فيما يلي كيفية إجراء اختبار z المكون من عينتين باستخدام هذه البيانات:

الخطوة الأولى: اذكر الفرضية الصفرية والبديلة.

أولاً سنذكر الفرضيتين الصفرية والبديلة:

• H ₀ : μ ₁ = μ ₂ (متوسطا السكان متساويان)
• H ₁ : μ ₁ ≠ μ ₂ (وسطا السكان غير متساويين)

الخطوة 2: احسب قيمة z.

بعد ذلك، سنقوم بإجراء اختبار z مكون من عينتين في برنامج Excel باستخدام هذه البيانات ونجد أن قيمة z هي -1.71817 .

الخطوة 3: احسب القيمة الاحتمالية.

يمكننا استخدام حاسبة القيمة P من Z إلى P لنجد أن القيمة p التي تتوافق مع القيمة az التي تبلغ -1.71817 هي 0.08577.

وبما أن هذه القيمة الاحتمالية لا تقل عن 0.05، فليس لدينا أدلة كافية لرفض فرضية العدم.

وهكذا نستنتج أن متوسط مستوى الذكاء لا يختلف كثيرا بين المدينتين.

لاحظ أننا استخدمنا ببساطة القيمة z كخطوة وسيطة لحساب القيمة p.

القيمة p هي القيمة الحقيقية التي كنا مهتمين بها، ولكن كان علينا حساب القيمة z أولاً.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إجراء اختبارات z باستخدام برامج إحصائية متنوعة:

كيفية إجراء اختبارات Z في Excel
كيفية إجراء اختبارات Z في R
كيفية إجراء اختبارات Z في بايثون