كيفية تفسير الخطأ المعياري المتبقي

يتم استخدام الخطأ القياسي المتبقي لقياس مدى ملاءمة نموذج الانحدار لمجموعة البيانات.

بعبارات بسيطة، فهو يقيس الانحراف المعياري للقيم المتبقية في نموذج الانحدار.

يتم حسابه على النحو التالي:

الخطأ المعياري المتبقي = √ Σ(y – ŷ) ² /df

ذهب:

• ذ: القيمة المرصودة
• ŷ: القيمة المتوقعة
• df: درجات الحرية، محسوبة على أنها إجمالي عدد الملاحظات – إجمالي عدد معلمات النموذج.

كلما كان الخطأ المعياري المتبقي أصغر، كان نموذج الانحدار يناسب مجموعة البيانات بشكل أفضل. على العكس من ذلك، كلما ارتفع الخطأ المعياري المتبقي، كلما كان نموذج الانحدار مناسبًا لمجموعة البيانات.

نموذج الانحدار الذي يحتوي على خطأ قياسي متبقي صغير سيكون له نقاط بيانات متجمعة بإحكام حول خط الانحدار الملائم:

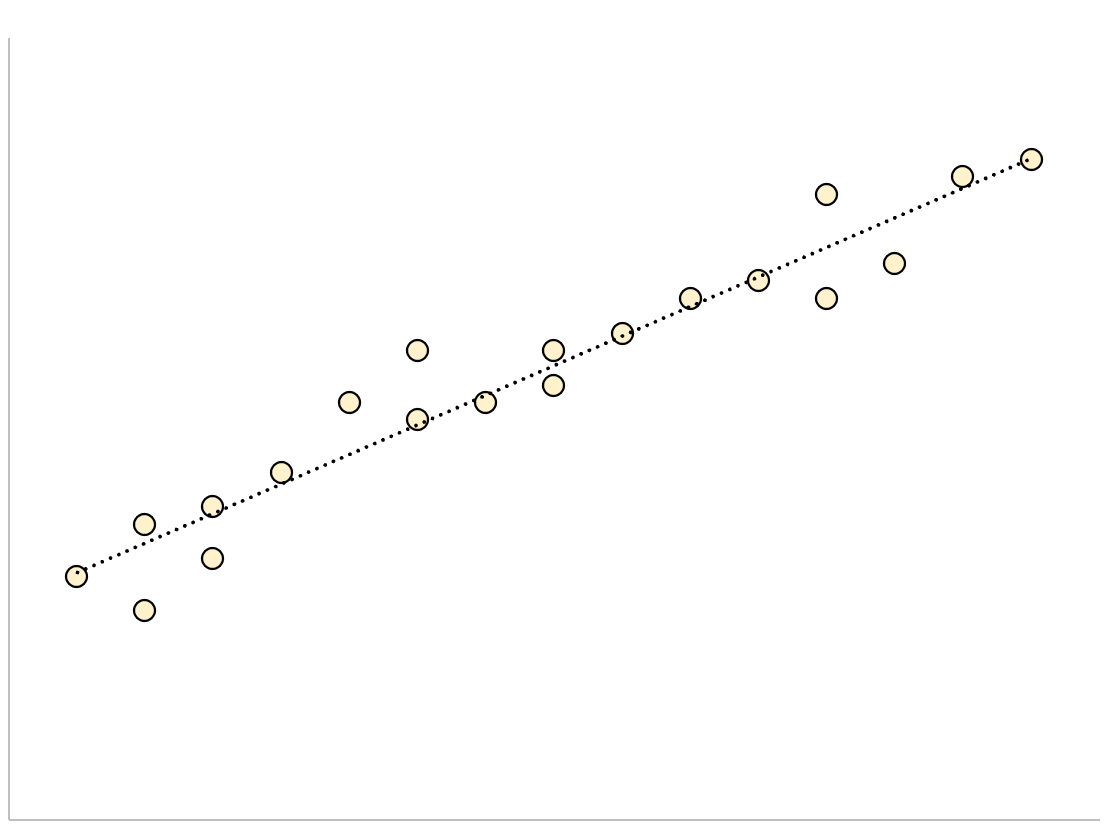
وستكون بقايا هذا النموذج (الفرق بين القيم المرصودة والقيم المتوقعة) صغيرة، أي أن الخطأ المعياري المتبقي سيكون صغيراً أيضاً.

على العكس من ذلك، فإن نموذج الانحدار الذي يحتوي على خطأ قياسي متبقي كبير سيكون له نقاط بيانات متناثرة بشكل فضفاض حول خط الانحدار الملائم:

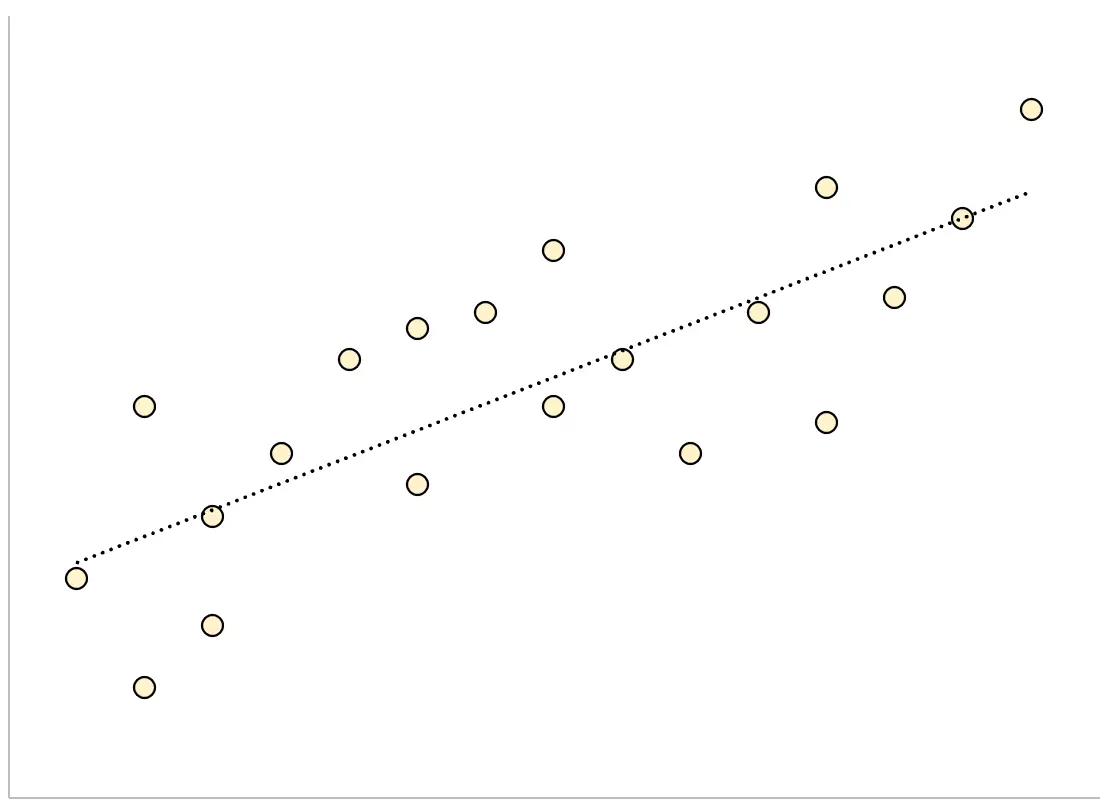
وستكون البقايا من هذا النموذج أكبر، مما يعني أن الخطأ المعياري المتبقي سيكون أكبر أيضًا.

يوضح المثال التالي كيفية حساب وتفسير الخطأ المعياري المتبقي لنموذج الانحدار في R.

مثال: تفسير الخطأ المعياري المتبقي

لنفترض أننا نريد ملاءمة نموذج الانحدار الخطي المتعدد التالي:

ميلا في الغالون = β ₀ + β ₁ (الإزاحة) + β ₂ (الطاقة)

يستخدم هذا النموذج متغيرات التوقع “الإزاحة” و”القوة الحصانية” للتنبؤ بالأميال لكل جالون تقطعه سيارة معينة.

يوضح الكود التالي كيفية ملاءمة نموذج الانحدار هذا في R:

 #load built-in mtcars dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

في الجزء السفلي من النتيجة، يمكننا أن نرى أن الخطأ المعياري المتبقي لهذا النموذج هو 3.127 .

يخبرنا هذا أن نموذج الانحدار يتنبأ بالميل لكل جالون في السيارة بمتوسط خطأ يبلغ حوالي 3,127.

استخدام الخطأ المعياري المتبقي لمقارنة النماذج

يعد الخطأ القياسي المتبقي مفيدًا بشكل خاص لمقارنة ملاءمة نماذج الانحدار المختلفة.

على سبيل المثال، لنفترض أننا قمنا بتركيب نموذجين مختلفين من نماذج الانحدار للتنبؤ بالميل لكل جالون في السيارة. الخطأ المعياري المتبقي لكل نموذج هو كما يلي:

• الخطأ المعياري المتبقي للنموذج 1: 3.127
• الخطأ المعياري المتبقي للنموذج 2: 5.657

نظرًا لأن النموذج 1 يحتوي على خطأ قياسي متبقي أقل، فإنه يناسب البيانات بشكل أفضل من النموذج 2. وبالتالي، نفضل استخدام النموذج 1 للتنبؤ بالميل لكل جالون في السيارة، لأن التنبؤات التي يقدمها أقرب إلى قيم ميل لكل جالون للسيارات.

مصادر إضافية

كيفية إجراء الانحدار الخطي البسيط في R
كيفية إجراء الانحدار الخطي المتعدد في R
كيفية إنشاء قطعة أرض متبقية في R