كيفية حساب vif في إكسل

تحدث العلاقة الخطية المتعددة في تحليل الانحدار عندما يرتبط متغيران تفسيريان أو أكثر ارتباطًا وثيقًا ببعضهما البعض، بحيث لا يوفران معلومات فريدة أو مستقلة في نموذج الانحدار. إذا كانت درجة الارتباط عالية بما يكفي بين المتغيرات، فقد يتسبب ذلك في حدوث مشكلات عند ملاءمة نموذج الانحدار وتفسيره.

لحسن الحظ، من الممكن اكتشاف العلاقة الخطية المتعددة باستخدام مقياس يسمى عامل تضخم التباين (VIF) ، والذي يقيس الارتباط وقوة الارتباط بين المتغيرات التوضيحية في نموذج الانحدار.

يشرح هذا البرنامج التعليمي كيفية حساب VIF في Excel.

مثال: حساب VIF في Excel

في هذا المثال، سنقوم بإجراء انحدار خطي متعدد باستخدام مجموعة البيانات التالية التي تصف سمات 10 من لاعبي كرة السلة. سوف نقوم بتركيب نموذج الانحدار باستخدام التصنيف كمتغير الاستجابة والنقاط والتمريرات والمرتدات كمتغيرات توضيحية. بعد ذلك، سوف نقوم بتحديد قيم VIF لكل متغير توضيحي.

الخطوة 1: تنفيذ الانحدار الخطي المتعدد.

في الشريط العلوي، انتقل إلى علامة التبويب “البيانات” وانقر فوق “تحليل البيانات”. إذا لم تشاهد هذا الخيار، فيجب عليك أولاً تثبيت برنامج Analysis ToolPak المجاني .

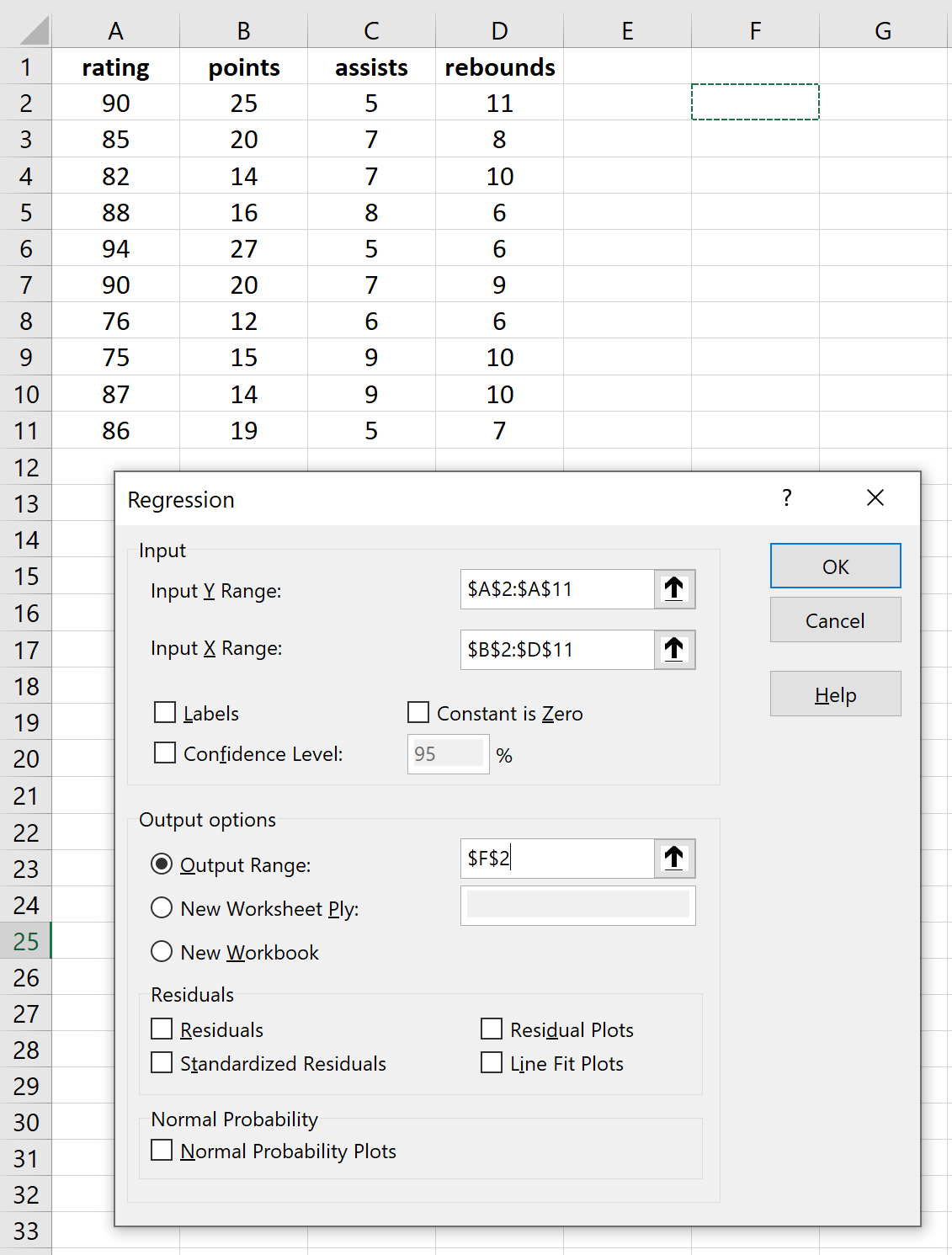
بمجرد النقر على تحليل البيانات، ستظهر نافذة جديدة. حدد الانحدار وانقر فوق موافق.

أكمل الجداول اللازمة لمتغيرات الاستجابة والمتغيرات التوضيحية، ثم انقر فوق موافق.

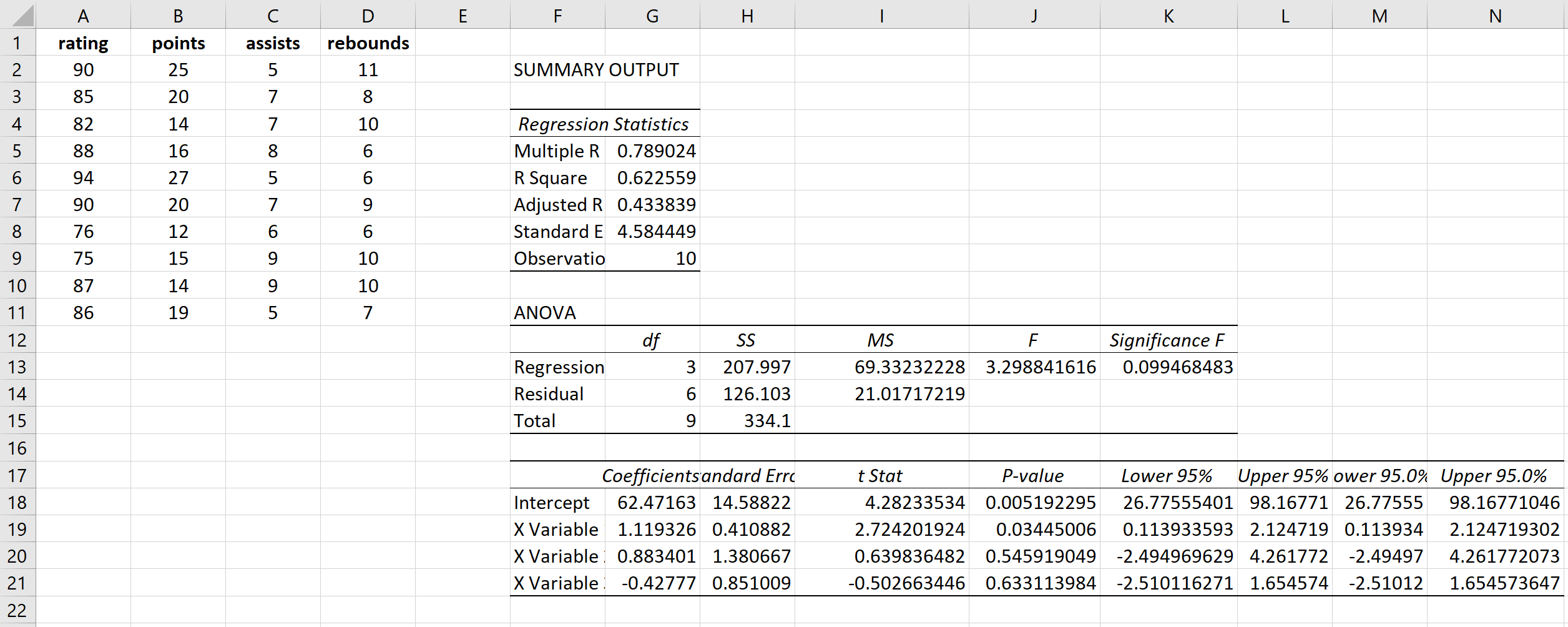
وهذا ينتج النتيجة التالية:

الخطوة 2: حساب VIF لكل متغير توضيحي.

بعد ذلك، يمكننا حساب VIF لكل من المتغيرات التوضيحية الثلاثة عن طريق إجراء انحدارات فردية باستخدام متغير توضيحي واحد كمتغير الاستجابة والمتغيرين الآخرين كمتغيرين توضيحيين.

على سبيل المثال، يمكننا حساب VIF لمتغير النقاط عن طريق إجراء انحدار خطي متعدد باستخدام النقاط كمتغير الاستجابة والمساعدات والارتدادات كمتغيرات توضيحية.

وهذا ينتج النتيجة التالية:

يتم حساب VIF للنقاط على النحو التالي: 1 / (1 – مربع R) = 1 / (1 – 0.433099) = 1.76 .

يمكننا بعد ذلك تكرار هذه العملية للمتغيرين الآخرين، التمريرات الحاسمة والمرتدات .

وتبين أن VIFs للمتغيرات التفسيرية الثلاثة هي كما يلي:

النقاط: 1.76
التمريرات الحاسمة: 1.96
المرتدات: 1.18

كيفية تفسير قيم VIF

تبدأ قيمة VIF عند 1 وليس لها حد أعلى. القاعدة العامة لتفسير VIFs هي:

• تشير القيمة 1 إلى عدم وجود ارتباط بين متغير توضيحي معين وأي متغير توضيحي آخر في النموذج.
• تشير القيمة بين 1 و5 إلى وجود علاقة معتدلة بين متغير توضيحي معين والمتغيرات التوضيحية الأخرى في النموذج، ولكنها في كثير من الأحيان ليست شديدة بما يكفي لتتطلب اهتماما خاصا.
• تشير القيمة الأكبر من 5 إلى وجود علاقة محتملة شديدة بين متغير توضيحي معين ومتغيرات توضيحية أخرى في النموذج. في هذه الحالة، من المحتمل أن تكون تقديرات المعامل والقيم الاحتمالية في نتائج الانحدار غير موثوقة.

نظرًا لأن كل قيمة من قيم VIF للمتغيرات التوضيحية في نموذج الانحدار الخاص بنا قريبة من 1، فإن التعددية الخطية ليست مشكلة في مثالنا.