كيفية قراءة مصفوفة الارتباط

في الإحصاء، نسعى غالبًا إلى فهم العلاقة بين متغيرين.

على سبيل المثال، قد نرغب في فهم العلاقة بين عدد الساعات التي يدرسها الطالب والدرجة التي يحصل عليها في الامتحان.

إحدى طرق قياس هذه العلاقة هي استخدام معامل ارتباط بيرسون ، وهو مقياس للارتباط الخطي بين متغيرين . لها قيمة بين -1 و 1 حيث:

• يشير -1 إلى وجود علاقة خطية سلبية تمامًا بين متغيرين
• يشير 0 إلى عدم وجود علاقة خطية بين متغيرين
• يشير الشكل 1 إلى وجود علاقة خطية إيجابية تمامًا بين متغيرين

وكلما زاد معامل الارتباط عن الصفر، كلما كانت العلاقة بين المتغيرين أقوى.

ذات صلة: ما الذي يعتبر ارتباطًا “قويًا”؟

لكن في بعض الحالات، نريد أن نفهم العلاقة بين أزواج متعددة من المتغيرات. في هذه الحالات يمكننا إنشاء مصفوفة الارتباط ، وهي عبارة عن جدول مربع يوضح معاملات الارتباط بين عدة متغيرات.

مثال مصفوفة الارتباط

تعرض مصفوفة الارتباط أدناه معاملات الارتباط بين العديد من المتغيرات المتعلقة بالتعليم:

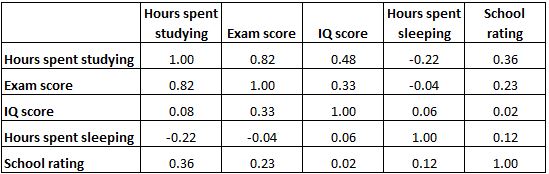
توضح كل خلية في الجدول العلاقة بين متغيرين محددين. على سبيل المثال، توضح الخلية المميزة أدناه أن الارتباط بين “الساعات التي يقضيها في الدراسة” و”درجة الامتحان” هو 0.82 ، مما يشير إلى أنهما مرتبطان بشكل إيجابي قوي. ترتبط الساعات الإضافية التي تقضيها في الدراسة ارتباطًا وثيقًا بدرجات الامتحانات الأعلى.

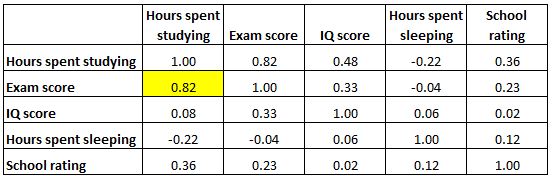
وتظهر الخلية الموضحة أدناه أن الارتباط بين “ساعات الدراسة” و”ساعات النوم” هو -0.22 ، مما يشير إلى أنهما مرتبطان بشكل سلبي ضعيف. ترتبط الساعات الإضافية التي يتم قضاؤها في الدراسة بساعات أقل في النوم.

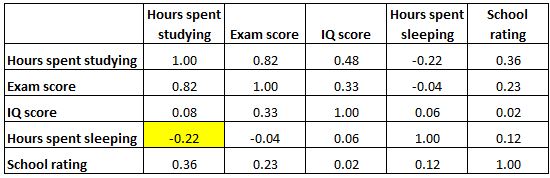
وتظهر الخلية الموضحة أدناه أن العلاقة بين “ساعات النوم” و”درجة الذكاء” هي 0.06 ، مما يشير إلى أنهما غير مرتبطين بشكل أساسي. هناك ارتباط ضئيل جدًا بين عدد الساعات التي ينامها الطالب ودرجة ذكائه.

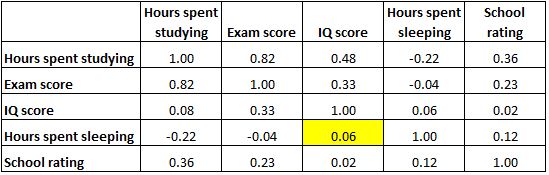
لاحظ أيضًا أن معاملات الارتباط على طول قطر الجدول تساوي 1 لأن كل متغير يرتبط تمامًا بنفسه. هذه الخلايا ليست مفيدة للتفسير.

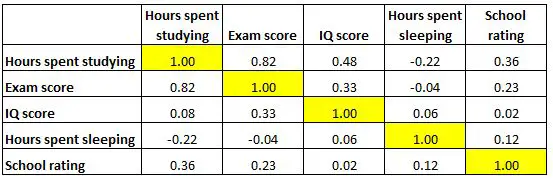
الاختلافات في مصفوفة الارتباط

لاحظ أن مصفوفة الارتباط متماثلة تمامًا. على سبيل المثال، تعرض الخلية العلوية اليمنى نفس القيمة تمامًا مثل الخلية اليسرى السفلية:

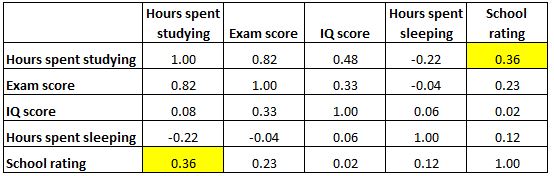
وبالفعل، تقيس الخليتان العلاقة بين “الساعات التي يقضيها المذاكرة” و”الصف الدراسي”.

نظرًا لأن مصفوفة الارتباط متماثلة، فإن نصف معاملات الارتباط المعروضة في المصفوفة زائدة عن الحاجة وغير ضرورية. لذلك، في بعض الأحيان سيتم عرض نصف مصفوفة الارتباط فقط:

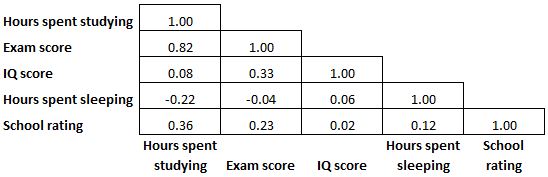
وفي بعض الأحيان يتم تلوين مصفوفة الارتباط مثل الخريطة الحرارية لتسهيل قراءة معاملات الارتباط:

متى تستخدم مصفوفة الارتباط

من الناحية العملية، يتم استخدام مصفوفة الارتباط بشكل شائع لثلاثة أسباب:

1. تلخص مصفوفة الارتباط بشكل ملائم مجموعة من البيانات.

مصفوفة الارتباط هي طريقة بسيطة لتلخيص الارتباطات بين جميع المتغيرات في مجموعة البيانات. على سبيل المثال، لنفترض أن لدينا مجموعة البيانات التالية التي تحتوي على المعلومات التالية لـ 1000 طالب:

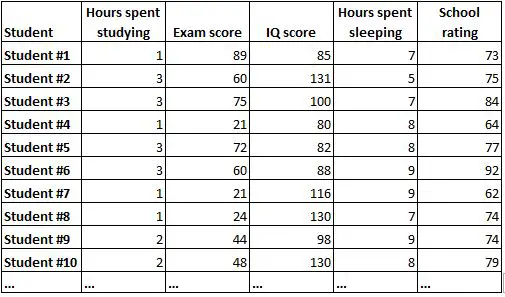
سيكون من الصعب جدًا فهم العلاقة بين كل متغير بمجرد النظر إلى البيانات الأولية. ولحسن الحظ، يمكن لمصفوفة الارتباط أن تساعدنا على فهم الارتباطات بين كل زوج من المتغيرات بسرعة.

2. تعمل مصفوفة الارتباط كتشخيص للانحدار.

أحد الافتراضات الرئيسية للانحدار الخطي المتعدد هو أنه لا يوجد متغير مستقل في النموذج يرتبط بقوة مع أي متغير آخر في النموذج.

عندما يكون هناك ارتباط كبير بين متغيرين مستقلين، يؤدي ذلك إلى مشكلة تسمى العلاقة الخطية المتعددة ويمكن أن تجعل من الصعب تفسير نتائج الانحدار.

إحدى أبسط الطرق لاكتشاف مشكلة وجود علاقة خطية متعددة محتملة هي النظر إلى مصفوفة الارتباط والتحقق بصريًا مما إذا كان أي من المتغيرات مرتبطًا بشكل كبير مع بعضها البعض.

3. يمكن استخدام مصفوفة الارتباط كمدخل لتحليلات أخرى.

يتم استخدام مصفوفة الارتباط كمدخل للتحليلات المعقدة الأخرى مثل تحليل العوامل الاستكشافية ونماذج المعادلات الهيكلية.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إنشاء مصفوفة ارتباط باستخدام برامج إحصائية متنوعة:

كيفية إنشاء مصفوفة الارتباط في إكسل
كيفية إنشاء مصفوفة الارتباط في SPSS
كيفية إنشاء مصفوفة الارتباط في ستاتا
كيفية إنشاء مصفوفة الارتباط في بايثون