كيندال تاو: تعريف + مثال

في الإحصاء، يشير الارتباط إلى قوة واتجاه العلاقة بين متغيرين. يمكن أن تتراوح قيمة معامل الارتباط من -1 إلى 1، حيث يشير -1 إلى علاقة سلبية كاملة، ويشير 0 إلى عدم وجود علاقة، ويشير 1 إلى علاقة إيجابية مثالية.

معامل الارتباط الأكثر استخدامًا هو معامل ارتباط بيرسون ، والذي يقيس الارتباط الخطي بين متغيرين عدديين.

معامل الارتباط الأقل استخدامًا هو Kendall’s Tau ، والذي يقيس العلاقة بين عمودين من البيانات المرتبة.

صيغة حساب Kendall’s Tau، والتي غالبًا ما يتم اختصارها بـ τ، هي كما يلي:

τ = (CD) / (C+D)

ذهب:

ج = عدد الأزواج المتطابقة

D = عدد الأزواج المتنافرة

يوضح المثال التالي كيفية استخدام هذه الصيغة لحساب معامل ارتباط رتبة Kendall’s Tau لعمودين من البيانات المرتبة.

مثال لحساب تاو كيندال

لنفترض أن اثنين من مدربي كرة السلة قاموا بترتيب 12 من لاعبيهم من الأسوأ إلى الأفضل. ويوضح الجدول التالي التصنيف الذي خصصه كل مدرب للاعبين:

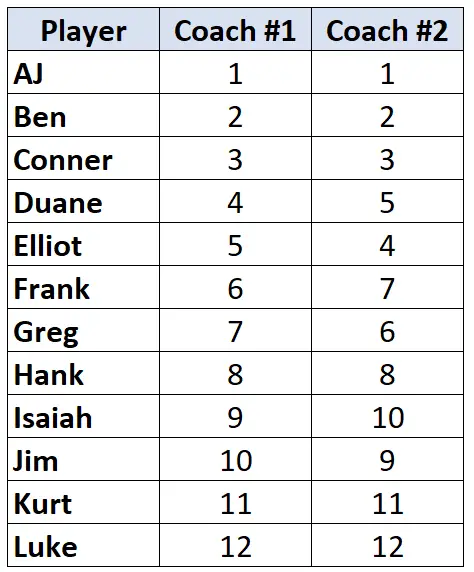
وبما أننا نعمل مع عمودين من البيانات المصنفة، فمن المناسب استخدام Kendall’s Tau لحساب الارتباط بين تصنيفات المدربين. اتبع الخطوات التالية لحساب تاو كيندال:

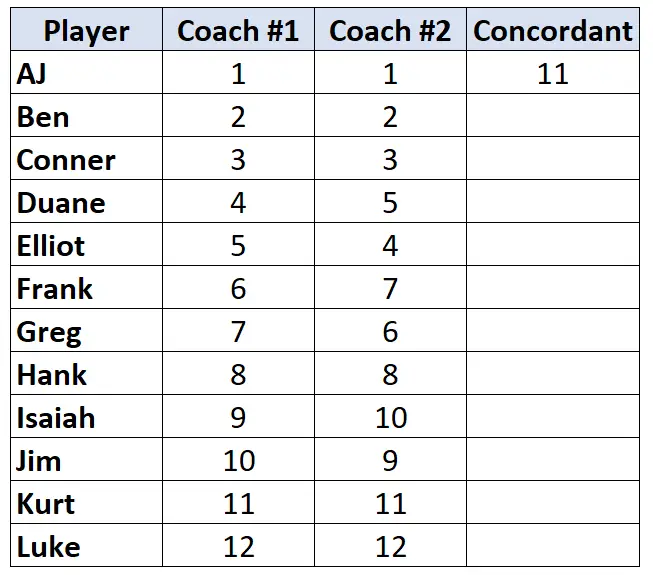
الخطوة 1: حساب عدد الأزواج المتطابقة.

انظر فقط إلى تصنيفات المدرب رقم 2. بدءًا من اللاعب الأول، قم بإحصاء عدد الرتب التي تحته والتي تكون أطول . على سبيل المثال، هناك 11 رقمًا أسفل “1” وهي أكبر، لذلك سنكتب 11:

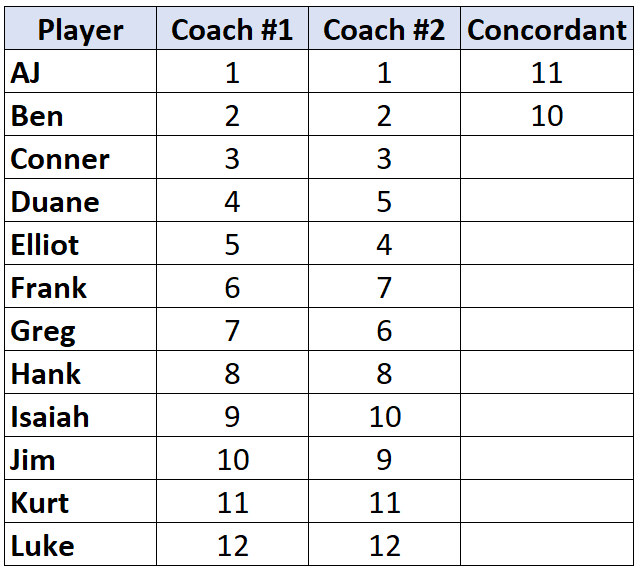
انتقل إلى اللاعب التالي وكرر العملية. هناك 10 أرقام أسفل الرقم 2 وهي أكبر، لذا سنكتب 10:

بمجرد أن نصل إلى لاعب تكون رتبته أقل من اللاعب الذي قبله، يتم تعيينه ببساطة نفس قيمة اللاعب الذي قبله. على سبيل المثال، حصل إليوت على رتبة “4” وهي أقل من رتبة اللاعب السابق “5”، لذلك تم تعيينه ببساطة بنفس قيمة اللاعب الذي سبقه:

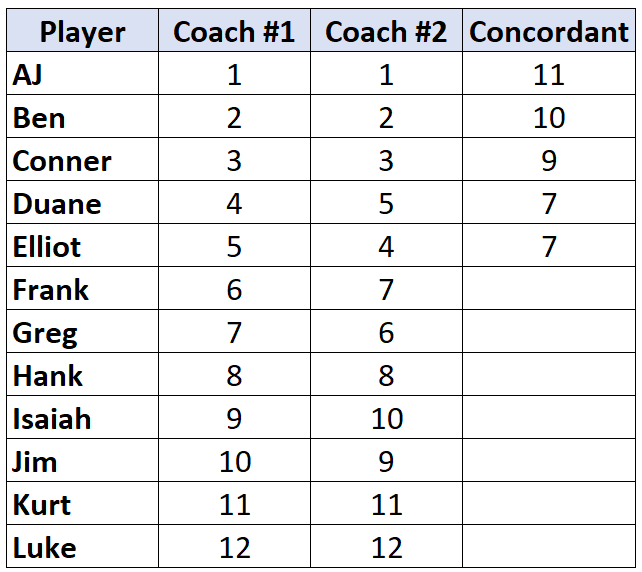
كرر هذه العملية لجميع اللاعبين:

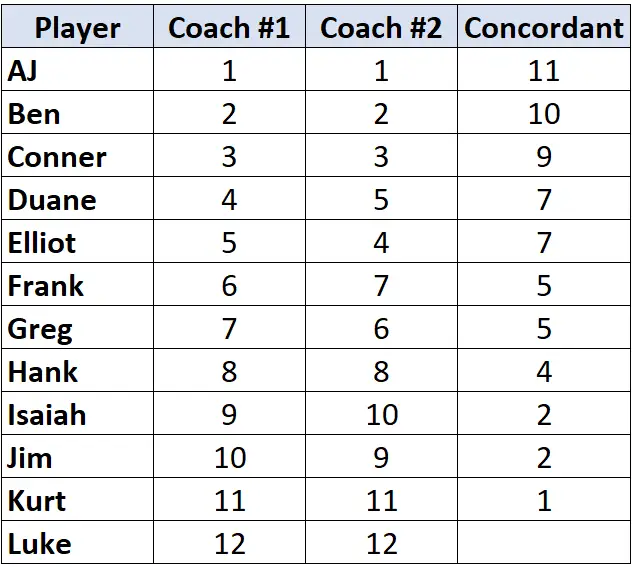
الخطوة 2: حساب عدد الأزواج المتنافرة.

مرة أخرى، انظر فقط إلى تصنيفات المدرب رقم 2. لكل لاعب، قم بإحصاء عدد الرتب الأدنى منه أو منها الأصغر . على سبيل المثال، قام المدرب رقم 2 بتعيين AJ بالرتبة “1” ولا يوجد لاعب أدنى منه يتمتع برتبة أقل. وبالتالي نعطيها القيمة 0:

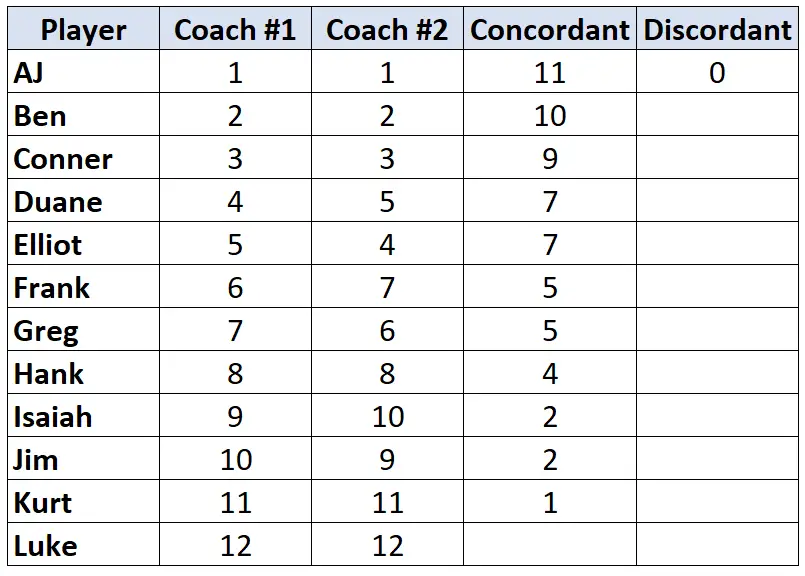
كرر هذه العملية لكل لاعب:

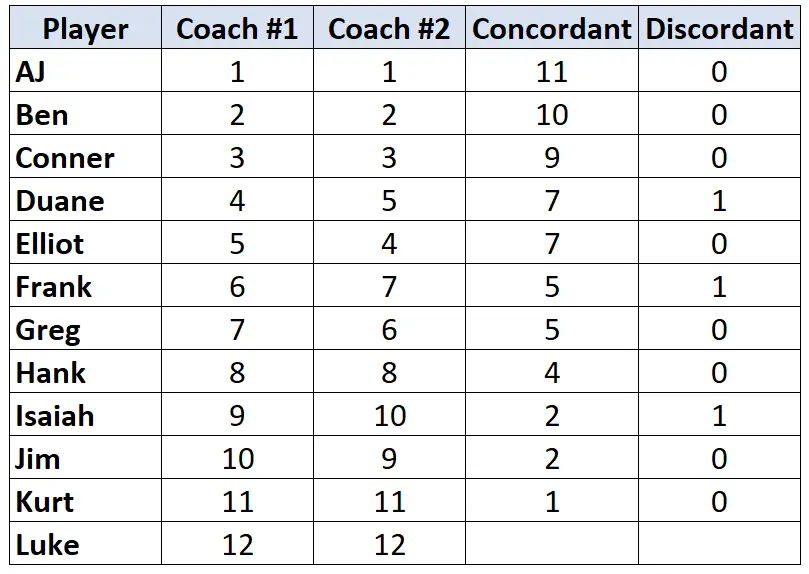
الخطوة 3: احسب مجموع كل عمود وابحث عن تاو كيندال.

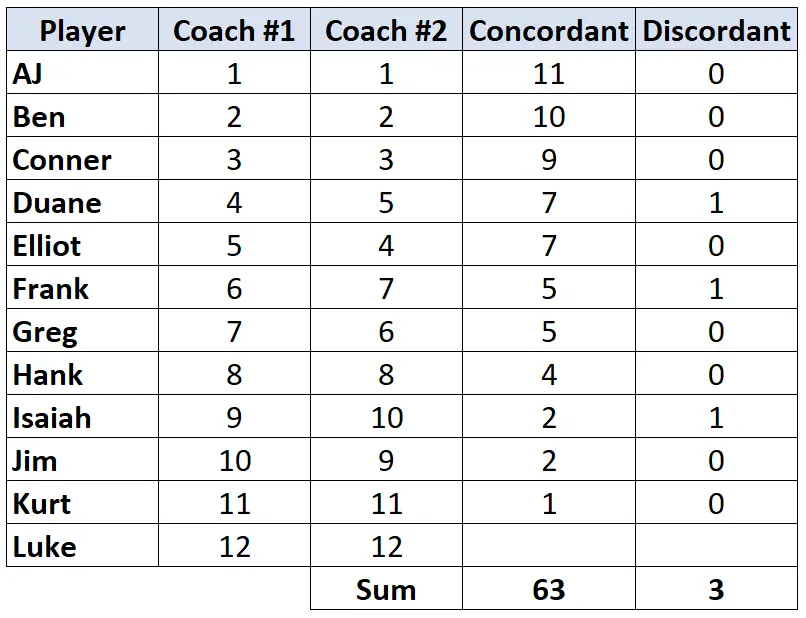
تاو كيندال = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0.909 .

الأهمية الإحصائية لتاو كيندال

عندما يكون لديك أكثر من n = 10 أزواج، يتبع Kendall’s Tau عمومًا التوزيع الطبيعي. يمكنك استخدام الصيغة التالية لحساب درجة z لـ Kendall’s Tau:

ض = 3τ*√ ن(ن-1) / √ 2(2ن+5)

ذهب:

τ = القيمة التي حسبتها لـ Kendall’s Tau

ن = عدد الأزواج

وإليك كيفية حساب z للمثال السابق:

ض = 3(.909)*√ 12(12-1) / √ 2(2*12+5) = 4.11 .

باستخدام حاسبة P-value Z-score، نرى أن القيمة p لهذه الدرجة z هي 0.00004 ، وهي ذات دلالة إحصائية عند مستوى 0.05 ألفا. وبالتالي توجد علاقة ارتباطية ذات دلالة إحصائية بين الرتب التي خصصها المدربان للاعبين.

المكافأة: كيفية حساب تاو كيندال في R

في برنامج إحصائيات R، يمكنك استخدام الدالة kendall.tau() من مكتبة VGAM لحساب Kendall’s Tau لمتجهين، والذي يستخدم الصيغة التالية:

كيندال.تاو (س، ص)

حيث x و y هما متجهان رقميان لهما نفس الطول.

يوضح الكود التالي كيفية حساب Kendall’s Tau للبيانات الدقيقة التي استخدمناها في المثال السابق:

 #load VGAM
library(VGAM)

#create vector for each coach's rankings
coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)
coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12)

#calculate Kendall's Tau
kendall.tau(coach_1, coach_2)

#[1] 0.9090909

لاحظ كيف تتطابق قيمة Kendall’s Tau مع القيمة التي حسبناها يدويًا.