لماذا تعتبر الإحصائيات مهمة؟ (10 أسباب تجعل الإحصائيات مهمة!)

يهتم مجال الإحصاء بجمع البيانات وتحليلها وتفسيرها وعرضها.

مع تزايد حضور التكنولوجيا في حياتنا اليومية، يتم إنشاء وجمع المزيد من البيانات أكثر من أي وقت مضى في تاريخ البشرية.

الإحصائيات هي المجال الذي يمكن أن يساعدنا في فهم كيفية استخدام هذه البيانات لأداء المهام التالية:

• فهم أفضل للعالم من حولنا.
• اتخاذ القرارات باستخدام البيانات.
• قم بالتنبؤ بالمستقبل باستخدام البيانات.

في هذه المقالة، نشارككم 10 أسباب تجعل مجال الإحصاء في غاية الأهمية في الحياة الحديثة.

السبب 1: استخدام الإحصائيات الوصفية لفهم العالم

تُستخدم الإحصائيات الوصفية لوصف جزء من البيانات الأولية. هناك ثلاثة أنواع رئيسية من الإحصاء الوصفي:

• احصائيات ملخصة
• الرسومات
• الطاولات

يمكن لكل عنصر من هذه العناصر أن يساعدنا على فهم البيانات الموجودة بشكل أفضل.

على سبيل المثال، لنفترض أن لدينا مجموعة بيانات أولية توضح درجات اختبار 10000 طالب في مدينة معينة. قد نستخدم الإحصائيات الوصفية من أجل:

• حساب متوسط درجات الاختبار والانحراف المعياري لنتائج الاختبار.
• قم بإنشاء رسم بياني أو مخطط مربع لتصور توزيع نتائج الاختبار.
• إنشاء جدول تكراري لفهم توزيع نتائج الاختبار.

باستخدام الإحصائيات الوصفية، يمكننا فهم درجات اختبار الطلاب بسهولة أكبر بكثير من مجرد النظر إلى البيانات الأولية.

السبب 2: احذر من الرسومات المضللة

يتم إنشاء المزيد والمزيد من الرسومات في المجلات ووسائل الإعلام والمقالات والمجلات عبر الإنترنت. لسوء الحظ، قد تكون المخططات مضللة في كثير من الأحيان إذا لم تفهم البيانات الأساسية.

على سبيل المثال، لنفترض أن إحدى المجلات تنشر دراسة وجدت وجود علاقة سلبية بين درجات GPA وACT للطلاب في جامعة معينة.

ومع ذلك، يحدث هذا الارتباط السلبي فقط لأن الطلاب الذين لديهم معدل تراكمي مرتفع ودرجة ACT قادرون على الالتحاق بجامعة النخبة، في حين لا يتم قبول الطلاب الذين لديهم معدل تراكمي منخفض ودرجة ACT على الإطلاق.

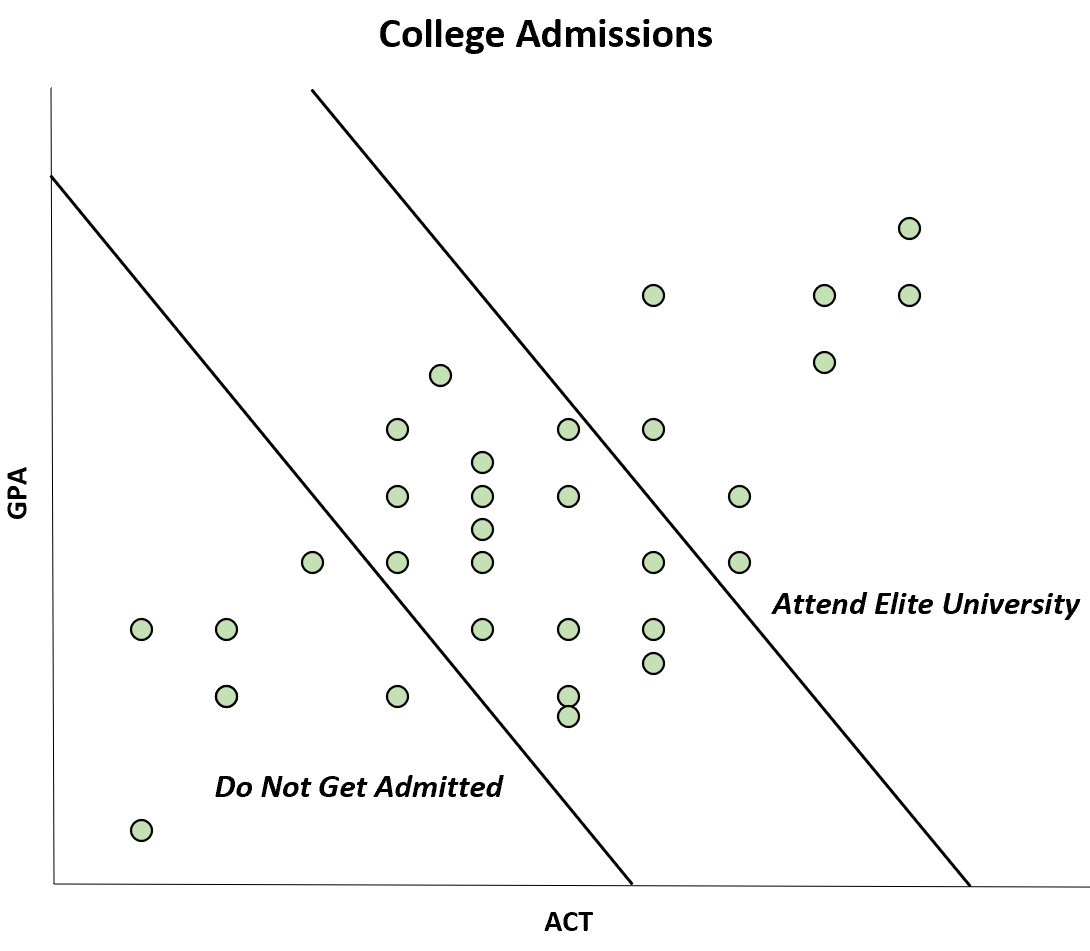
على الرغم من أن الارتباط بين ACT وGPA إيجابي في السكان، إلا أن الارتباط يبدو سلبيا في العينة.

يُعرف هذا التحيز الخاص باسم تحيز بيركسون . من خلال إدراك هذا التحيز، يمكنك تجنب التعرض للتضليل من خلال بعض الرسوم البيانية.

السبب 3: كن حذرًا من إرباك المتغيرات

من المفاهيم المهمة التي ستتعرف عليها في الإحصاء هو مفهوم المتغيرات المربكة .

هذه متغيرات لا تؤخذ في الاعتبار ويمكن أن تربك نتائج التجربة وتؤدي إلى استنتاجات غير موثوقة.

على سبيل المثال، لنفترض أن أحد الباحثين يجمع بيانات عن مبيعات الآيس كريم وهجمات أسماك القرش ويكتشف أن المتغيرين مترابطان بشكل كبير. هل هذا يعني أن زيادة مبيعات الآيس كريم تسبب المزيد من هجمات أسماك القرش؟

هذا غير محتمل. السبب الأكثر احتمالا هو درجة الحرارة المتغيرة المربكة. عندما يكون الجو أكثر دفئًا في الخارج، يشتري عدد أكبر من الأشخاص الآيس كريم ويذهب عدد أكبر من الأشخاص إلى المحيط.

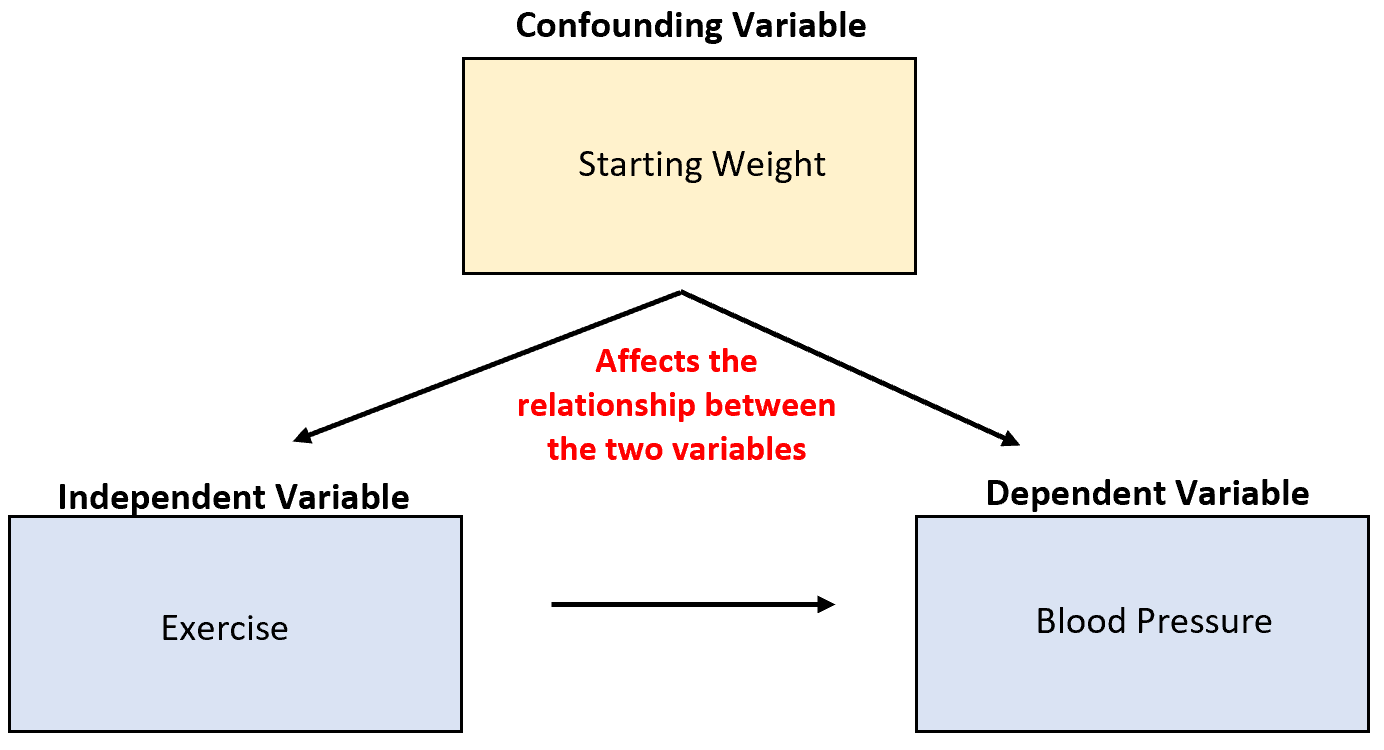
السبب 4: اتخاذ قرارات أفضل باستخدام الاحتمالات

أحد أهم المجالات الفرعية للإحصاء هو الاحتمال . وهو المجال الذي يدرس احتمالية وقوع الأحداث.

ومن خلال الفهم الأساسي للاحتمالات، يمكنك اتخاذ قرارات أكثر استنارة في العالم الحقيقي.

على سبيل المثال، لنفترض أن طالبًا في المدرسة الثانوية يعرف أن لديه فرصة 10% للقبول في جامعة معينة. باستخدام صيغة احتمال النجاح “واحدة على الأقل” ، يستطيع هذا الطالب إيجاد احتمال قبوله في جامعة واحدة على الأقل يتقدم إليها ويمكنه تعديل عدد الجامعات التي يتقدم إليها بالنتيجة.

السبب 5: فهم القيم P في البحث

هناك مفهوم مهم آخر ستتعرف عليه في الإحصائيات وهو القيم الاحتمالية .

التعريف الكلاسيكي للقيمة p هو:

القيمة p هي احتمالية مراقبة عينة إحصائية تكون على الأقل متطرفة مثل إحصائية العينة الخاصة بك، بشرط أن تكون فرضية العدم صحيحة.

على سبيل المثال، لنفترض أن أحد المصانع يدعي أنه ينتج إطارات يبلغ متوسط وزنها 200 رطل. يفترض أحد المدققين أن متوسط الوزن الفعلي للإطارات المنتجة في هذا المصنع يختلف بمقدار 200 رطل. لذلك أجرى اختبارًا فرضيًا ووجد أن القيمة p للاختبار هي 0.04.

إليك كيفية تفسير هذه القيمة p:

إذا كان المصنع ينتج بالفعل إطارات بمتوسط وزن 200 رطل، فإن 4% من جميع عمليات التدقيق ستحقق التأثير الملحوظ في العينة، أو أكثر، بسبب خطأ عشوائي في أخذ العينات. وهذا يخبرنا أن الحصول على بيانات العينة التي حصل عليها المدقق سيكون نادرًا جدًا إذا كان المصنع ينتج بالفعل إطارات يبلغ متوسط وزنها 200 رطل.

وبالتالي، من المرجح أن يرفض المدقق الفرضية الصفرية القائلة بأن متوسط الوزن الفعلي للإطارات المنتجة في هذا المصنع يبلغ بالفعل 200 رطل.

السبب 6: فهم الارتباط

هناك مفهوم مهم آخر ستتعرف عليه في الإحصائيات وهو الارتباط ، والذي يخبرنا بالارتباط الخطي بين متغيرين.

تكون قيمة معامل الارتباط دائمًا بين -1 و1 حيث:

• يشير -1 إلى وجود علاقة خطية سلبية تمامًا بين متغيرين
• يشير 0 إلى عدم وجود علاقة خطية بين متغيرين
• يشير الشكل 1 إلى وجود علاقة خطية إيجابية تمامًا بين متغيرين

ومن خلال فهم هذه القيم، يمكنك فهم العلاقة بين المتغيرات في العالم الحقيقي.

على سبيل المثال، إذا كان الارتباط بين الإنفاق الإعلاني والإيرادات هو 0.87، فيمكنك أن تفهم أن هناك علاقة إيجابية قوية بين المتغيرين. عندما تنفق المزيد من الأموال على الإعلانات، يمكنك توقع زيادة متوقعة في الإيرادات.

السبب 7: عمل تنبؤات حول المستقبل

سبب آخر مهم لتعلم الإحصائيات هو فهم نماذج الانحدار الأساسية مثل:

• الانحدار الخطي البسيط
• الانحدار الخطي المتعدد
• الانحدار اللوجستي

يتيح لك كل نموذج من هذه النماذج إجراء تنبؤات حول القيمة المستقبلية لمتغير الاستجابة بناءً على قيمة متغيرات توقع معينة في النموذج.

على سبيل المثال، تستخدم الشركات نماذج الانحدار الخطي المتعددة في العالم الحقيقي طوال الوقت عند استخدام متغيرات التوقع مثل العمر والدخل والعرق وما إلى ذلك. للتنبؤ بعدد العملاء الذين سينفقون في متاجرهم.

وبالمثل، تستخدم شركات الخدمات اللوجستية متغيرات تنبؤية مثل إجمالي الطلب وحجم السكان وما إلى ذلك. للتنبؤ بالمبيعات المستقبلية.

بغض النظر عن المجال الذي تعمل فيه، هناك فرصة جيدة لاستخدام نماذج الانحدار للتنبؤ بظاهرة مستقبلية.

السبب 8: فهم التحيز المحتمل في الدراسات

سبب آخر لدراسة الإحصائيات هو أن تكون على دراية بجميع أنواع التحيز المختلفة التي يمكن أن تنشأ في دراسات العالم الحقيقي.

وهنا بعض الأمثلة:

• مراقبة التحيز
• التحيز في الاختيار الذاتي
• التحيز المرجعي
• تم حذف التحيز المتغير
• التحيز الناقص
• انحياز عدم الاستجابة

من خلال الفهم الأساسي لهذه الأنواع من التحيزات، يمكنك تجنب ارتكابها عند إجراء البحث أو أن تكون على دراية بها عند قراءة الأوراق البحثية أو الدراسات الأخرى.

السبب 9: فهم الافتراضات التي وضعتها الاختبارات الإحصائية

تضع العديد من الاختبارات الإحصائية افتراضات حول البيانات الأساسية التي تتم دراستها.

عند قراءة نتائج دراسة ما أو حتى إجراء دراستك الخاصة، من المهم أن تفهم الافتراضات التي يجب وضعها حتى تكون النتائج موثوقة.

تشترك المقالات التالية في الافتراضات التي تم وضعها في العديد من الاختبارات والإجراءات الإحصائية شائعة الاستخدام:

• ما هو افتراض التباين المتساوي في الإحصاء؟
• ما هو الافتراض الطبيعي في الإحصاء؟
• ما هو افتراض الاستقلال في الإحصاء؟

السبب العاشر: تجنب التعميم الزائد

سبب آخر لدراسة الإحصائيات هو فهم مفهوم التعميم الزائد .

ويحدث هذا عندما لا يمثل الأفراد المشاركون في الدراسة أفرادًا في إجمالي عدد السكان، وبالتالي فمن غير المناسب تعميم نتائج الدراسة على جميع السكان.

على سبيل المثال، لنفترض أننا نريد معرفة النسبة المئوية للطلاب في مدرسة معينة يفضلون “الدراما” كنوع من الأفلام المفضلة لديهم. إذا كان إجمالي عدد الطلاب عبارة عن مزيج من 50% فتيان و50% فتيات، فإن العينة التي تتكون من 90% فتيان و10% فتيات يمكن أن تؤدي إلى نتائج متحيزة إذا كان عدد أقل بكثير من الأولاد يفضلون المسرح كنوع مفضل.

ومن الناحية المثالية، نريد أن تشبه عينتنا “نسخة مصغرة” من سكاننا. وبالتالي، إذا كان إجمالي عدد الطلاب يتكون من 50% فتيات و50% فتيان، فلن تكون عينتنا ممثلة إذا كانت تشمل 90% فتيان و10% فتيات فقط.

لذلك، سواء كنت تجري المسح الخاص بك أو تقرأ نتائج المسح، فمن المهم أن تفهم ما إذا كانت بيانات العينة تمثل إجمالي السكان وما إذا كان من الممكن تعميم نتائج المسح على السكان بثقة.

مصادر إضافية

راجع المقالات التالية للحصول على فهم أساسي لأهم المفاهيم في الإحصاءات التمهيدية:

الإحصاء الوصفي أو الاستدلالي
السكان مقابل عينة
الإحصائيات مقابل المعلمات
المتغيرات النوعية والكمية
مستويات القياس: الاسمية والترتيبية والفاصلة والنسبة