ماي مقابل. rmse: ما هو المقياس الذي يجب عليك استخدامه؟

تُستخدم نماذج الانحدار لتحديد العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة .

عندما نلائم نموذج الانحدار، نريد أن نفهم مدى قدرة النموذج على استخدام قيم متغيرات التوقع للتنبؤ بقيمة متغير الاستجابة.

هناك مقياسان نستخدمهما غالبًا لتحديد مدى ملاءمة النموذج لمجموعة بيانات هما متوسط الخطأ المطلق (MAE) وجذر متوسط مربع الخطأ (RMSE)، والتي يتم حسابها على النحو التالي:

MAE : مقياس يخبرنا بمتوسط الفرق المطلق بين القيم المتوقعة والقيم الفعلية في مجموعة البيانات. كلما انخفض MAE، كان النموذج مناسبًا لمجموعة البيانات بشكل أفضل.

MAE = 1/n * Σ|y _i – ŷ _i |

ذهب:

• Σ هو رمز يعني “المجموع”
• y _i هي القيمة المرصودة للملاحظة ⁱ
• ŷ _i هي القيمة المتوقعة ^{للملاحظة} i
• n هو حجم العينة

RMSE : مقياس يخبرنا بالجذر التربيعي لجذر متوسط مربع الفرق بين القيم المتوقعة والقيم الفعلية في مجموعة البيانات. كلما انخفض RMSE، كلما كان النموذج مناسبًا لمجموعة البيانات بشكل أفضل.

يتم حسابه على النحو التالي:

RMSE = √ Σ(y _i – ŷ _i ) ² / n

ذهب:

• Σ هو رمز يعني “المجموع”
• ŷ _i هي القيمة المتوقعة ^{للملاحظة} i
• y _i هي القيمة المرصودة للملاحظة ⁱ
• n هو حجم العينة

مثال: حساب RMSE وMAE

لنفترض أننا نستخدم نموذج الانحدار للتنبؤ بعدد النقاط التي سيسجلها 10 لاعبين في مباراة كرة السلة.

والجدول التالي يوضح النقاط التي تنبأ بها النموذج مقارنة بالنقاط الفعلية التي سجلها اللاعبون:

باستخدام الآلة الحاسبة MAE، يمكننا حساب أن MAE يساوي 3.2.

وهذا يخبرنا أن متوسط الفرق المطلق بين القيم التي تنبأ بها النموذج والقيم الفعلية هو 3.2.

باستخدام الآلة الحاسبة RMSE ، يمكننا حساب أن RMSE يساوي 4 .

يخبرنا هذا أن الجذر التربيعي لجذر متوسط الفروق المربعة بين النقاط المسجلة المتوقعة والنقاط المسجلة الفعلية هو 4.

لاحظ أن كل مقياس يعطينا فكرة عن الفرق النموذجي بين القيمة المتوقعة التي قدمها النموذج والقيمة الفعلية في مجموعة البيانات، ولكن تفسير كل مقياس يختلف قليلاً.

RMSE مقابل MAE: ما هو المقياس الذي يجب عليك استخدامه؟

إذا كنت تريد تعيين وزن أكبر للملاحظات الأبعد عن المتوسط (أي إذا كان الانحراف بمقدار 20 أكثر سوءًا من الانحراف بمقدار 10)، فمن الأفضل استخدام RMSE لقياس الخطأ، لأن RMSE هو أكثر حساسية للملاحظات أبعد من المتوسط.

ومع ذلك، إذا كان “الإزاحة” عند 20 أسوأ بمرتين من “الإزاحة” عند 10، فمن الأفضل استخدام MAE.

لتوضيح ذلك، لنفترض أن لدينا لاعبًا استثنائيًا بشكل واضح من حيث عدد النقاط المسجلة:

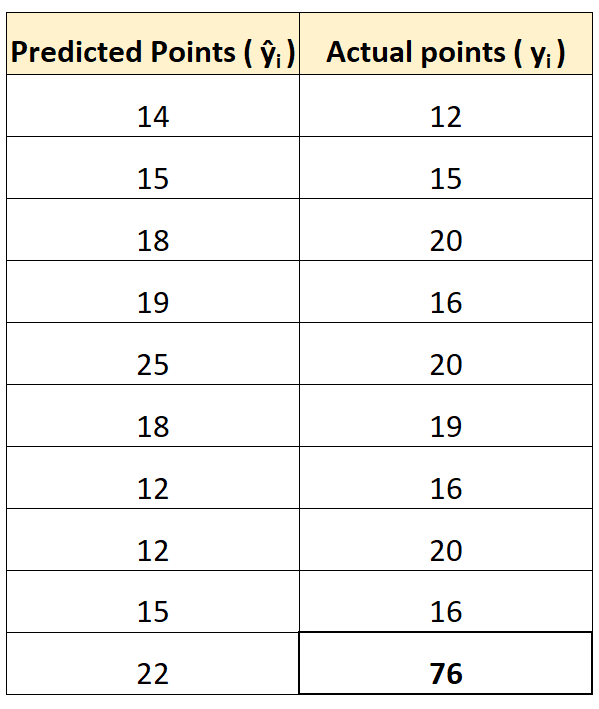
باستخدام الآلات الحاسبة الموجودة على الإنترنت المذكورة سابقًا، يمكننا حساب MAE وRMSE على النحو التالي:

• ماي : 8
• آر إم إس إي : 16.4356

لاحظ أن RMSE يزيد بكثير عن MAE.

وذلك لأن RMSE يستخدم فروقًا مربعة في صيغته والفرق التربيعي بين القيمة المرصودة البالغة 76 والقيمة المتوقعة البالغة 22 كبير جدًا. وينتج عن هذا زيادة كبيرة في قيمة RMSE.

من الناحية العملية، نقوم عادةً بتناسب نماذج الانحدار المتعددة مع مجموعة بيانات ونحسب واحدًا فقط من هذه المقاييس لكل نموذج.

على سبيل المثال، يمكننا ملاءمة ثلاثة نماذج انحدار مختلفة وحساب RMSE لكل نموذج. سنقوم بعد ذلك باختيار النموذج ذو أقل قيمة RMSE باعتباره النموذج “الأفضل”، لأنه النموذج الذي يجعل التنبؤات أقرب إلى القيم الفعلية في مجموعة البيانات.

وفي كلتا الحالتين، تأكد فقط من حساب نفس المقياس لكل نموذج. على سبيل المثال، لا تحسب MAE لنموذج واحد وRMSE لنموذج آخر ثم تقارن هذين القياسين.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية حساب MAE باستخدام برامج إحصائية مختلفة:

كيفية حساب يعني الخطأ المطلق في Excel
كيفية حساب الخطأ المطلق في R
كيفية حساب متوسط الخطأ المطلق في بايثون

تشرح البرامج التعليمية التالية كيفية حساب RMSE باستخدام برامج إحصائية مختلفة:

كيفية حساب متوسط الخطأ المربع في إكسل
كيفية حساب متوسط الخطأ التربيعي في R
كيفية حساب متوسط الخطأ التربيعي في بايثون