ما هي العلاقة الخطية المتعددة المثالية؟ (تعريف وأمثلة)

في الإحصاء، تحدث العلاقة الخطية المتعددة عندما يكون هناك ارتباط بين متغيرين أو أكثر من متغيرات التنبؤ بشكل كبير، بحيث لا توفر معلومات فريدة أو مستقلة في نموذج الانحدار.

إذا كانت درجة الارتباط عالية بما يكفي بين المتغيرات، فقد يتسبب ذلك في حدوث مشكلات عند ملاءمة نموذج الانحدار وتفسيره.

الحالة الأكثر تطرفًا للتعددية الخطية تسمى التعددية الخطية المثالية . يحدث هذا عندما يكون لمتغيرين أو أكثر علاقة خطية دقيقة مع بعضهما البعض.

على سبيل المثال، لنفترض أن لدينا مجموعة البيانات التالية:

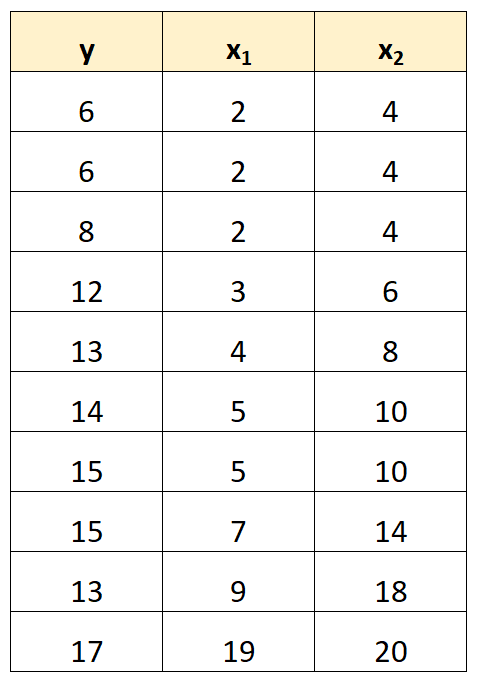
لاحظ أن قيم المتغير المتنبئ _x2 هي ببساطة قيم _x1 مضروبة في 2.

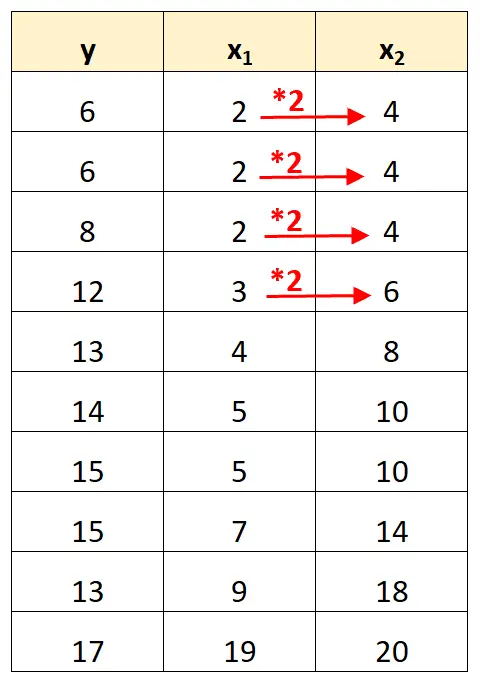
وهذا مثال على التعددية الخطية المثالية .

مشكلة التعددية الخطية المثالية

عند وجود علاقة خطية متعددة مثالية في مجموعة بيانات، فإن المربعات الصغرى العادية غير قادرة على إنتاج تقديرات لمعاملات الانحدار.

في الواقع، ليس من الممكن تقدير التأثير الهامشي لمتغير متنبئ (x ₁ ) على متغير الاستجابة (y) مع الحفاظ على متغير متنبئ آخر (x ₂ ) ثابتًا لأن x ₂ يتحرك دائمًا بالضبط عندما يتحرك x ₁ .

باختصار، فإن التعددية الخطية المثالية تجعل من المستحيل تقدير قيمة لكل معامل في نموذج الانحدار.

كيفية التعامل مع التعددية المثالية

إن أبسط طريقة للتعامل مع العلاقة الخطية المتعددة المثالية هي إزالة أحد المتغيرات التي لها علاقة خطية دقيقة مع متغير آخر.

على سبيل المثال، في مجموعة البيانات السابقة، يمكننا ببساطة إزالة x ₂ كمتغير متوقع.

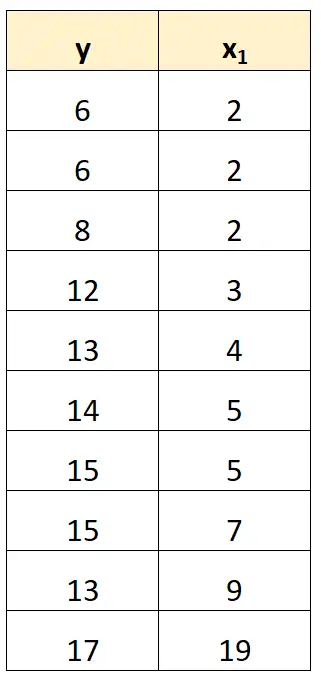
سنقوم بعد ذلك بتركيب نموذج الانحدار باستخدام x ₁ كمتغير متنبئ و y كمتغير الاستجابة.

أمثلة على التعددية الخطية المثالية

توضح الأمثلة التالية السيناريوهات الثلاثة الأكثر شيوعًا للعلاقة الخطية المتعددة المثالية في الممارسة العملية.

1. المتغير المتنبئ هو مضاعف لمتغير آخر

لنفترض أننا نريد استخدام “الارتفاع بالسنتيمتر” و”الارتفاع بالأمتار” للتنبؤ بوزن نوع معين من الدلافين.

هذا ما قد تبدو عليه مجموعة البيانات لدينا:

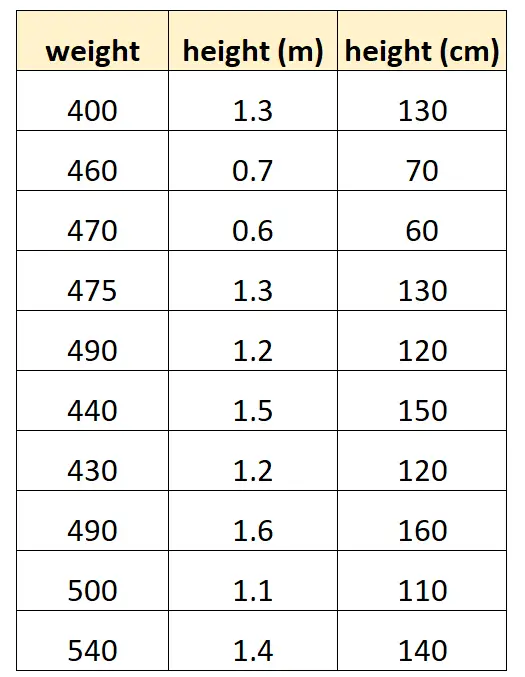
لاحظ أن قيمة “الارتفاع بالسنتيمتر” تساوي ببساطة “الارتفاع بالمتر” مضروبًا في 100. هذه حالة تعدد خطي مثالي.

إذا حاولنا ملاءمة نموذج الانحدار الخطي المتعدد في R باستخدام مجموعة البيانات هذه، فلن نتمكن من إنتاج تقدير معامل لمتغير التوقع “الأمتار”:

 #define data
df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
                 m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
                 cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))

#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)

#view summary of model
summary(model)

Call:
lm(formula = weight ~ m + cm, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-70,501 -25,501 5,183 19,499 68,590 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 458,676 53,403 8,589 2.61e-05 ***
m 9.096 43.473 0.209 0.839    
cm NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 
F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395

2. المتغير المتنبئ هو نسخة محولة من متغير آخر

لنفترض أننا نريد استخدام “النقاط” و”النقاط المقاسة” للتنبؤ بتقييم لاعبي كرة السلة.

لنفترض أن المتغير “النقاط المقاسة” يتم حسابه على النحو التالي:

النقاط المقاسة = (النقاط – μ _النقاط ) / σ _النقاط

هذا ما قد تبدو عليه مجموعة البيانات لدينا:

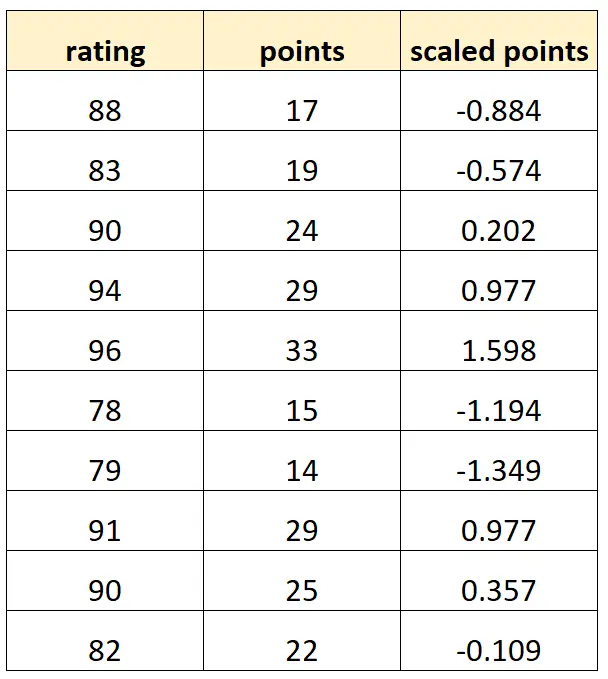
لاحظ أن كل قيمة من “النقاط المقاسة” هي ببساطة نسخة موحدة من “النقاط”. هذه هي حالة التعددية الخطية المثالية.

إذا حاولنا ملاءمة نموذج الانحدار الخطي المتعدد في R باستخدام مجموعة البيانات هذه، فلن نتمكن من إنتاج تقدير معامل لمتغير التوقع “النقاط المقاسة”:

 #define data
df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
                 pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))

df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)

#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)

#view summary of model
summary(model)

Call:
lm(formula = rating ~ pts + scaled_pts, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4932 -1.3941 -0.2935 1.3055 5.8412 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 67.4218 3.5896 18.783 6.67e-08 ***
pts 0.8669 0.1527 5.678 0.000466 ***
scaled_pts NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 
F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663

3. المصيدة المتغيرة الوهمية

هناك سيناريو آخر يمكن أن يحدث فيه تعدد خطي مثالي يُعرف باسم مصيدة المتغير الوهمي . وذلك عندما نريد أن نأخذ متغيرًا فئويًا في نموذج الانحدار ونحوله إلى “متغير وهمي” يأخذ القيم 0، 1، 2، إلخ.

على سبيل المثال، لنفترض أننا نريد استخدام متغيرات التوقع “العمر” و”الحالة الاجتماعية” للتنبؤ بالدخل:

لاستخدام “الحالة الاجتماعية” كمتغير متوقع، يجب علينا أولاً تحويله إلى متغير وهمي.

للقيام بذلك، يمكننا ترك “أعزب” كقيمة أساسية، لأن هذا يحدث في أغلب الأحيان، وتعيين قيم 0 أو 1 لـ “متزوج” و”طلاق” على النحو التالي:

سيكون من الخطأ إنشاء ثلاثة متغيرات وهمية جديدة على النحو التالي:

في هذه الحالة، يكون المتغير “أعزب” عبارة عن مزيج خطي مثالي من المتغيرين “متزوج” و”مطلق”. هذا مثال على التعددية الخطية المثالية.

إذا حاولنا ملاءمة نموذج الانحدار الخطي المتعدد في R باستخدام مجموعة البيانات هذه، فلن نتمكن من إنتاج تقدير معامل لكل متغير متنبئ:

 #define data
df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
                 age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
                 single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
                 married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
                 divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))

#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)

#view summary of model
summary(model)

Call:
lm(formula = income ~ age + single + married + divorced, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-9.7075 -5.0338 0.0453 3.3904 12.2454 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 16.7559 17.7811 0.942 0.37739   
age 1.4717 0.3544 4.152 0.00428 **
single -2.4797 9.4313 -0.263 0.80018   
married NA NA NA NA   
divorced -8.3974 12.7714 -0.658 0.53187   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 
F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865

مصادر إضافية

دليل للتعددية الخطية وVIF في الانحدار
كيفية حساب VIF في R
كيفية حساب VIF في بايثون
كيفية حساب VIF في إكسل