R متعددة أو r مربع: ما هو الفرق؟

عندما تناسب نموذج الانحدار باستخدام معظم البرامج الإحصائية، ستلاحظ غالبًا القيمتين التاليتين في النتيجة:

R المتعددة: معامل الارتباط المتعدد بين ثلاثة متغيرات أو أكثر.

R-Square: يتم حسابه على أنه (Multiple R) ² ويمثل نسبة التباين في متغير الاستجابة لنموذج الانحدار الذي يمكن تفسيره بواسطة المتغيرات المتوقعة. تتراوح هذه القيمة من 0 إلى 1.

من الناحية العملية، غالبًا ما نهتم بقيمة R-squared لأنها تخبرنا بمدى فائدة متغيرات التوقع في التنبؤ بقيمة متغير الاستجابة.

ومع ذلك، في كل مرة نضيف فيها متغيرًا متوقعًا جديدًا إلى النموذج، يتم ضمان زيادة R-squared حتى لو لم يكن المتغير المتوقع مفيدًا.

إن R-squared المعدل هو نسخة معدلة من R-squared والتي يتم ضبطها حسب عدد المتنبئين في نموذج الانحدار. يتم حسابه على النحو التالي:

تم تعديل R ² = 1 – [(1-R ² )*(n-1)/(nk-1)]

ذهب:

• R ² : R ² للنموذج
• n : عدد الملاحظات
• k : عدد المتغيرات المتوقعة

نظرًا لأن R-squared يزداد دائمًا كلما أضفت المزيد من المتنبئين إلى النموذج، يمكن أن يكون R-squared المعدل بمثابة مقياس يخبرك بمدى فائدة النموذج، ويتم تعديله بناءً على عدد المتنبئين في النموذج .

لفهم كل مصطلح من هذه المصطلحات بشكل أفضل، خذ بعين الاعتبار المثال التالي.

مثال: R المتعددة، R-squared وR-squared المعدلة

لنفترض أن لدينا مجموعة البيانات التالية التي تحتوي على المتغيرات الثلاثة التالية لـ 12 طالبًا مختلفًا:

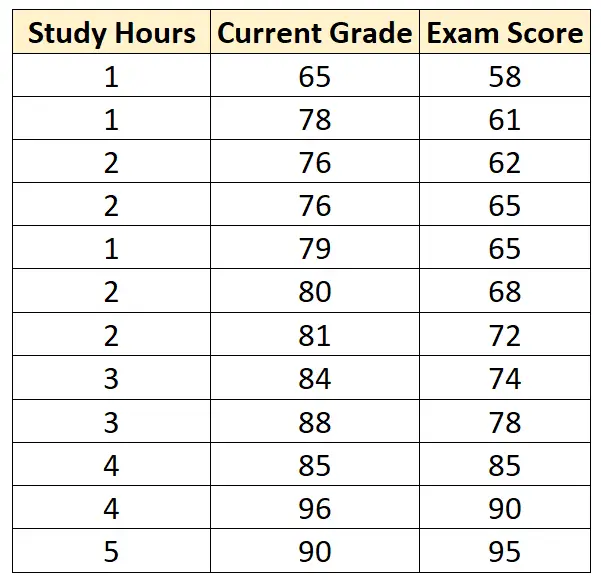
لنفترض أننا نلائم نموذج الانحدار الخطي المتعدد باستخدام ساعات الدراسة والصف الحالي كمتغيرات متوقعة ودرجة الامتحان كمتغير الاستجابة ونحصل على النتيجة التالية:

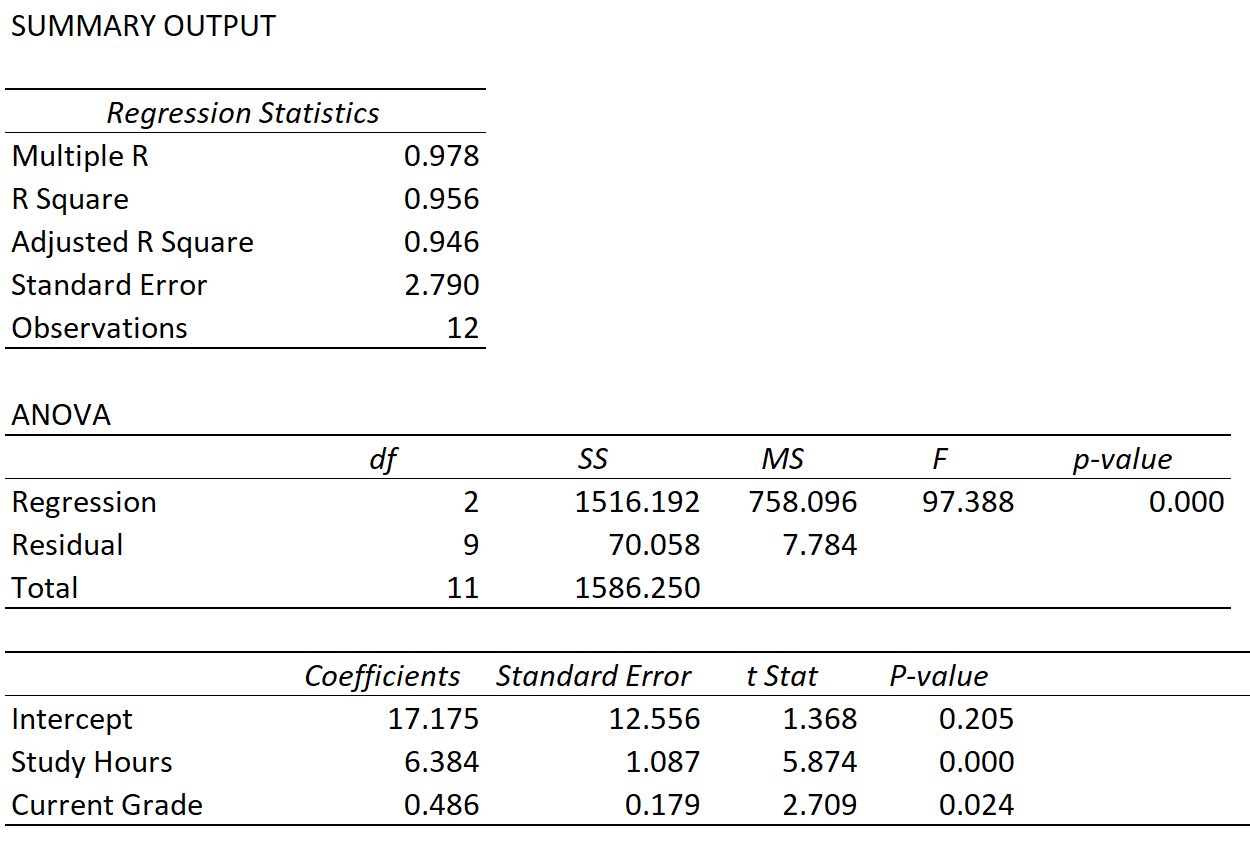
يمكننا ملاحظة قيم المقاييس الثلاثة التالية:

متعددة ر: 0.978 . ويمثل هذا الارتباط المتعدد بين متغير الاستجابة والمتغيرين المتنبئين.

ساحة آر : 0.956 . يتم حساب ذلك على النحو التالي (متعدد R) ² = (0.978) ² = 0.956. وهذا يخبرنا أن 95.6% من التباين في درجات الامتحان يمكن تفسيره بعدد الساعات التي قضاها الطلاب في الدراسة ودرجاتهم الحالية في المقرر.

تعديل مربع R: 0.946 . ويتم حساب ذلك على النحو التالي:

تم تعديل R ² = 1 – [(1-R ² )*(n-1)/(nk-1)] = 1 – [(1-.956)*(12-1)/(12-2-1) ] = 0.946.

ويمثل هذا قيمة R-squared، المعدلة لعدد المتغيرات المتوقعة في النموذج .

سيكون هذا المقياس مفيدًا، على سبيل المثال، إذا قمنا بتركيب نموذج انحدار آخر يحتوي على 10 تنبؤات ووجدنا أن مربع R المعدل لهذا النموذج كان 0.88 . قد يشير هذا إلى أن نموذج الانحدار الذي يحتوي على اثنين فقط من المتنبئين أفضل لأنه يحتوي على قيمة مربعة R معدلة أعلى.

مصادر إضافية

مقدمة في الانحدار الخطي المتعدد
ما هي قيمة R-squared الجيدة؟