كيفية استخدام المتغيرات الوهمية في تحليل الانحدار
الانحدار الخطي هو أسلوب يمكننا استخدامه لقياس العلاقة بين واحد أو أكثر من متغيرات التوقع ومتغير الاستجابة .
نستخدم عمومًا الانحدار الخطي مع المتغيرات الكمية . تسمى أحيانًا بالمتغيرات “الرقمية”، وهي متغيرات تمثل كمية قابلة للقياس. الامثله تشمل:
- عدد الأمتار المربعة في المنزل
- الحجم السكاني للمدينة
- عمر الفرد
ومع ذلك، في بعض الأحيان نرغب في استخدام المتغيرات الفئوية كمتغيرات تنبؤية. هذه هي المتغيرات التي تأخذ أسماء أو تسميات ويمكن أن تندرج في فئات. الامثله تشمل:
- لون العين (على سبيل المثال “أزرق”، “أخضر”، “بني”)
- الجنس (على سبيل المثال “رجل”، “امرأة”)
- الحالة الاجتماعية (على سبيل المثال “متزوج”، “أعزب”، “مطلق”)
عند استخدام المتغيرات الفئوية، ليس من المنطقي تخصيص قيم مثل 1، 2، 3 لقيم مثل “الأزرق” و”الأخضر” و”البني” فقط، لأنه ليس من المنطقي قول ذلك أن اللون الأخضر مزدوج . ملون مثل اللون الأزرق أو البني أكثر لونًا بثلاث مرات من اللون الأزرق.
بدلا من ذلك، الحل هو استخدام المتغيرات الوهمية . هذه هي المتغيرات التي نقوم بإنشائها خصيصًا لتحليل الانحدار والتي تأخذ إحدى القيمتين: صفر أو واحد.
المتغيرات الوهمية: المتغيرات الرقمية المستخدمة في تحليل الانحدار لتمثيل البيانات الفئوية التي يمكن أن تأخذ واحدة فقط من القيمتين: صفر أو واحد.
عدد المتغيرات الوهمية التي نحتاج إلى إنشائها يساوي k -1 حيث k هو عدد القيم المختلفة التي يمكن أن يأخذها المتغير الفئوي.
توضح الأمثلة التالية كيفية إنشاء متغيرات وهمية لمجموعات بيانات مختلفة.
المثال 1: إنشاء متغير وهمي بقيمتين فقط
لنفترض أن لدينا مجموعة البيانات التالية ونريد استخدام الجنس والعمر للتنبؤ بالدخل :
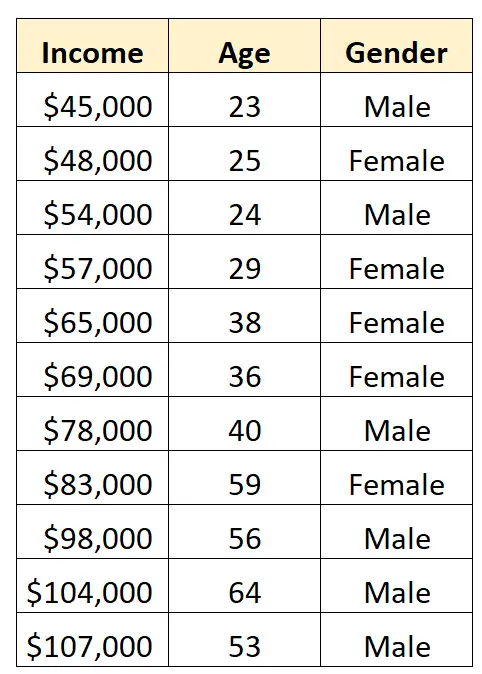
لاستخدام الجنس كمتغير متوقع في نموذج الانحدار، نحتاج إلى تحويله إلى متغير وهمي.
نظرًا لأن هذا متغير فئة حاليًا يمكن أن يأخذ قيمتين مختلفتين (“ذكر” أو “أنثى”)، فإننا ببساطة ننشئ k -1 = 2-1 = 1 متغير وهمي.
لإنشاء هذا المتغير الوهمي، يمكننا اختيار إحدى القيمتين (“ذكر” أو “أنثى”) لتمثل 0 والأخرى لتمثل 1.
بشكل عام، عادةً ما نمثل القيمة الأكثر شيوعًا بالرقم 0، والذي سيكون “ذكر” في مجموعة البيانات هذه.
لذا، إليك كيفية تحويل الجنس إلى متغير وهمي:
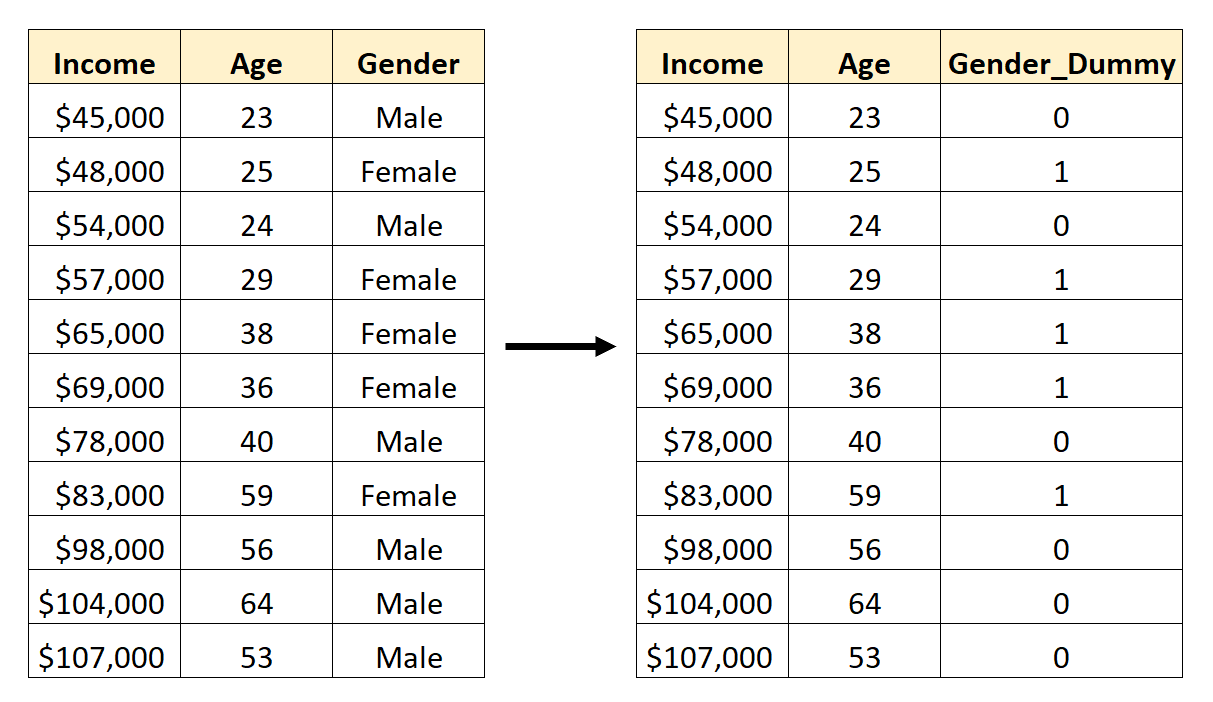
يمكننا بعد ذلك استخدام Age و Gender_Dummy كمتغيرات تنبؤية في نموذج الانحدار.
المثال 2: إنشاء متغير وهمي بقيم متعددة
لنفترض أن لدينا مجموعة البيانات التالية ونريد استخدام الحالة الاجتماعية والعمر للتنبؤ بالدخل :

لاستخدام الحالة الاجتماعية كمتغير متوقع في نموذج الانحدار، نحتاج إلى تحويله إلى متغير وهمي.
نظرًا لأن هذا متغير فئة حاليًا يمكن أن يأخذ ثلاث قيم مختلفة (“أعزب” أو “متزوج” أو “مطلق”)، فنحن بحاجة إلى إنشاء k -1 = 3-1 = 2 متغيرات وهمية.
لإنشاء هذا المتغير الوهمي، يمكننا ترك “مفرد” كقيمة أساسية لأنه يظهر في أغلب الأحيان. إذن، إليك كيفية تحويل الحالة الاجتماعية إلى متغيرات وهمية:

يمكننا بعد ذلك استخدام العمر والمتزوج والمطلق كمتغيرات تنبؤية في نموذج الانحدار.
كيفية تفسير مخرجات الانحدار باستخدام المتغيرات الوهمية
لنفترض أننا نلائم نموذج الانحدار الخطي المتعدد باستخدام مجموعة البيانات من المثال السابق مع العمر والمتزوج والمطلق كمتغيرات متوقعة والدخل كمتغير الاستجابة.
وهنا نتيجة الانحدار:
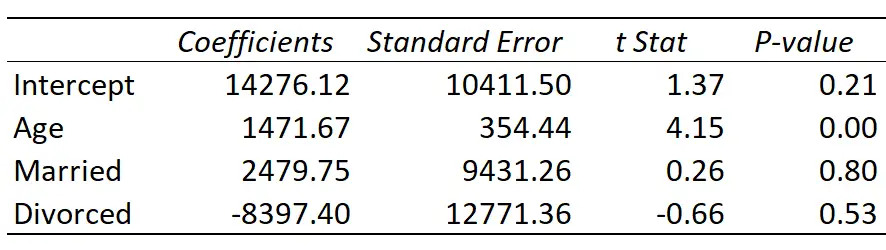
يتم تعريف خط الانحدار المجهز على النحو التالي:
الدخل = 14,276.21 + 1,471.67*(العمر) + 2,479.75*(متزوج) – 8,397.40*(مطلق)
يمكننا استخدام هذه المعادلة للعثور على الدخل المقدر للفرد بناءً على عمره وحالته الاجتماعية. على سبيل المثال، الشخص البالغ من العمر 35 عامًا والمتزوج سيكون لديه دخل يقدر بـ 68,264 دولارًا :
الدخل = 14,276.21 + 1,471.67*(35) + 2,479.75*(1) – 8,397.40*(0) = 68,264 دولارًا
فيما يلي كيفية تفسير معاملات الانحدار في الجدول:
- الاعتراض: يمثل الاعتراض متوسط دخل شخص واحد عمره صفر. من الواضح أنه لا يمكن أن يكون لديك صفر سنة، لذلك ليس من المنطقي تفسير التقاطع بمفرده في نموذج الانحدار المحدد هذا.
- العمر: ترتبط كل سنة من الزيادة في العمر بمتوسط زيادة قدرها 1,471.67 دولارًا في الدخل. وبما أن القيمة الاحتمالية (0.00) أقل من 0.05، فإن العمر يعد مؤشرًا مهمًا إحصائيًا للدخل.
- متزوج: يكسب الشخص المتزوج في المتوسط 2,479.75 دولارًا أكثر من الشخص الأعزب. وبما أن القيمة p (0.80) لا تقل عن 0.05، فإن هذا الفرق ليس ذا دلالة إحصائية.
- المطلق: يكسب الشخص المطلق في المتوسط 8,397.40 دولارًا أقل من الشخص الأعزب. وبما أن القيمة p (0.53) لا تقل عن 0.05، فإن هذا الفرق ليس ذا دلالة إحصائية.
وبما أن كلا المتغيرين الوهميين لم يكن لهما دلالة إحصائية، فيمكننا إزالة الحالة الاجتماعية كمتنبئ من النموذج، حيث لا يبدو أنها تضيف قيمة تنبؤية إلى الدخل.
مصادر إضافية
المتغيرات النوعية والكمية
المصيدة المتغيرة الوهمية
كيفية قراءة وتفسير جدول الانحدار
شرح القيم P والأهمية الإحصائية