متى يجب عليك استخدام الانحدار متعدد الحدود؟
الانحدار متعدد الحدود هو أسلوب يمكننا استخدامه لملاءمة نموذج الانحدار عندما تكون العلاقة بين متغير (متغيرات) التوقع ومتغير الاستجابة غير خطية.
يأخذ نموذج الانحدار متعدد الحدود الشكل التالي:
Y = β 0 + β 1 X + β 2 X 2 + … + β h
من الناحية العملية، هناك ثلاث طرق بسيطة لتحديد ما إذا كان يجب عليك استخدام الانحدار متعدد الحدود مقابل نموذج أبسط مثل الانحدار الخطي .
1. قم بإنشاء مخطط تشتت لمتغير التوقع ومتغير الاستجابة
أسهل طريقة لتحديد ما إذا كان يجب عليك استخدام الانحدار متعدد الحدود هي إنشاء مخطط تشتت بسيط لمتغير التوقع ومتغير الاستجابة.
على سبيل المثال، لنفترض أننا نريد استخدام المتغير المتنبئ “ساعات الدراسة” للتنبؤ بالدرجة التي سيحصل عليها الطالب في الاختبار النهائي.
قبل تركيب نموذج الانحدار، يمكننا أولاً إنشاء مخطط مبعثر للساعات التي تمت دراستها مقابل نتائج الامتحان. لنفترض أن مخطط التشتت الخاص بنا يبدو كالتالي:
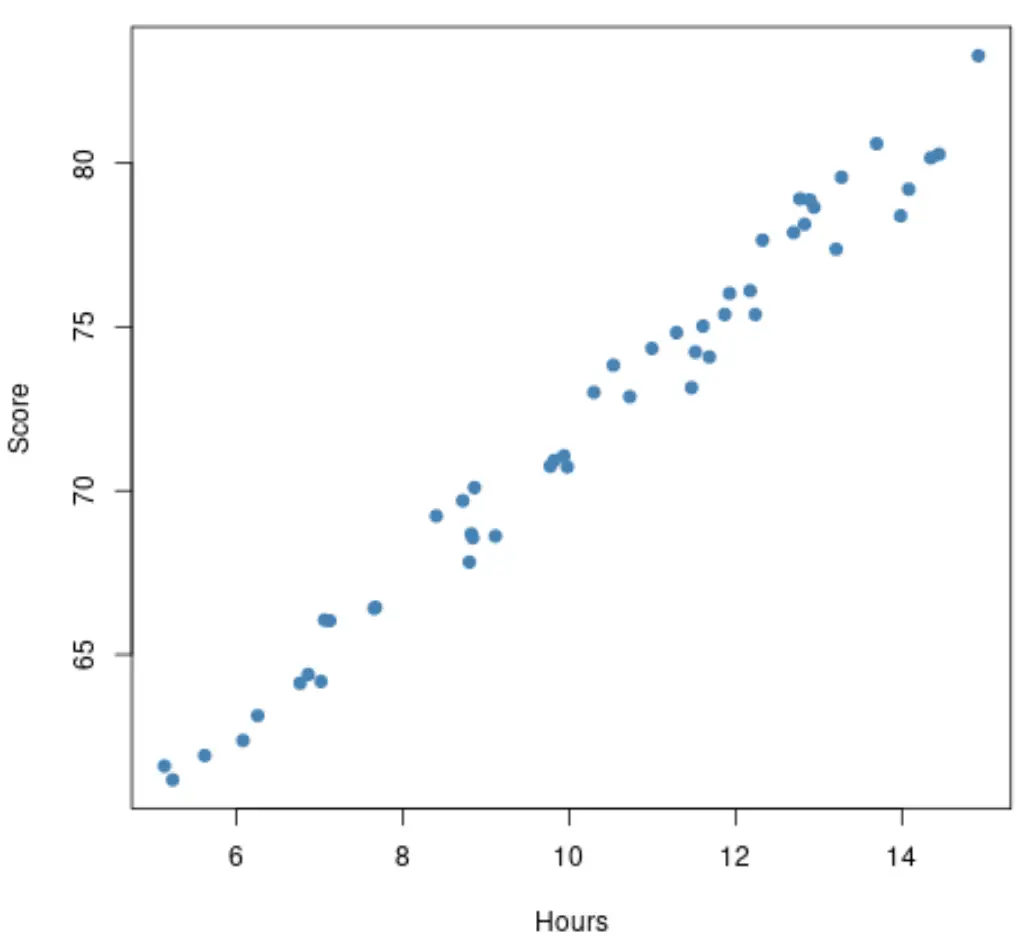
تظهر العلاقة بين ساعات الدراسة ونتائج الامتحانات خطية ، لذلك سيكون من المنطقي ملاءمة نموذج الانحدار الخطي البسيط لمجموعة البيانات هذه.
ومع ذلك، لنفترض أن مخطط التشتت يبدو في الواقع كما يلي:
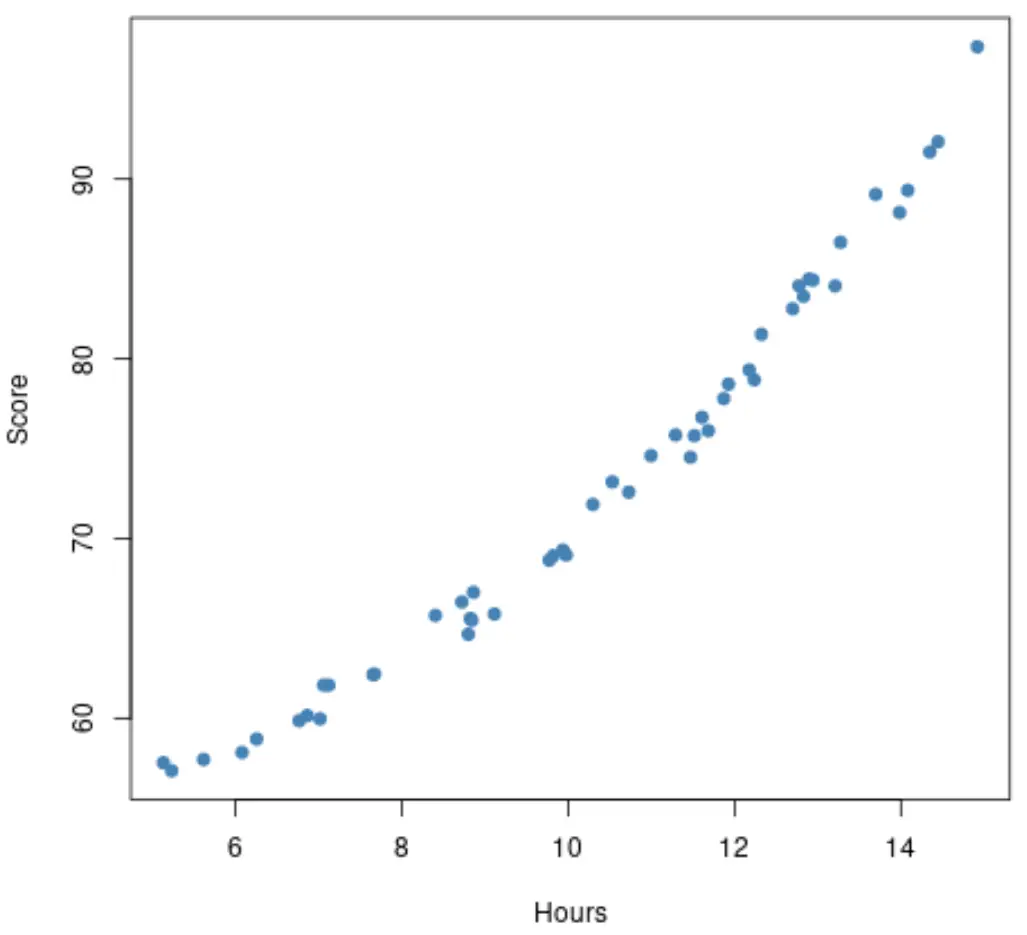
تبدو هذه العلاقة غير خطية إلى حد ما، مما يخبرنا أنه قد يكون من الحكمة أن نلائم نموذج الانحدار متعدد الحدود بدلاً من ذلك.
2. قم بإنشاء رسم بياني للقيم المجهزة والمتبقية
هناك طريقة أخرى لتحديد ما إذا كان يجب عليك استخدام الانحدار متعدد الحدود وهي ملاءمة نموذج الانحدار الخطي لمجموعة البيانات ثم إنشاء مخطط للقيم المجهزة مقابل القيم المتبقية للنموذج.
إذا كان هناك اتجاه غير خطي واضح في القيم المتبقية، فهذا يشير إلى أن الانحدار متعدد الحدود قد يوفر ملاءمة أفضل للبيانات.
على سبيل المثال، لنفترض أننا نلائم نموذج الانحدار الخطي باستخدام الساعات المدروسة كمتغير متوقع ودرجة الامتحان كمتغير الاستجابة، ثم نقوم بإنشاء المخطط التالي للقيم المجهزة مقابل القيم المتبقية:
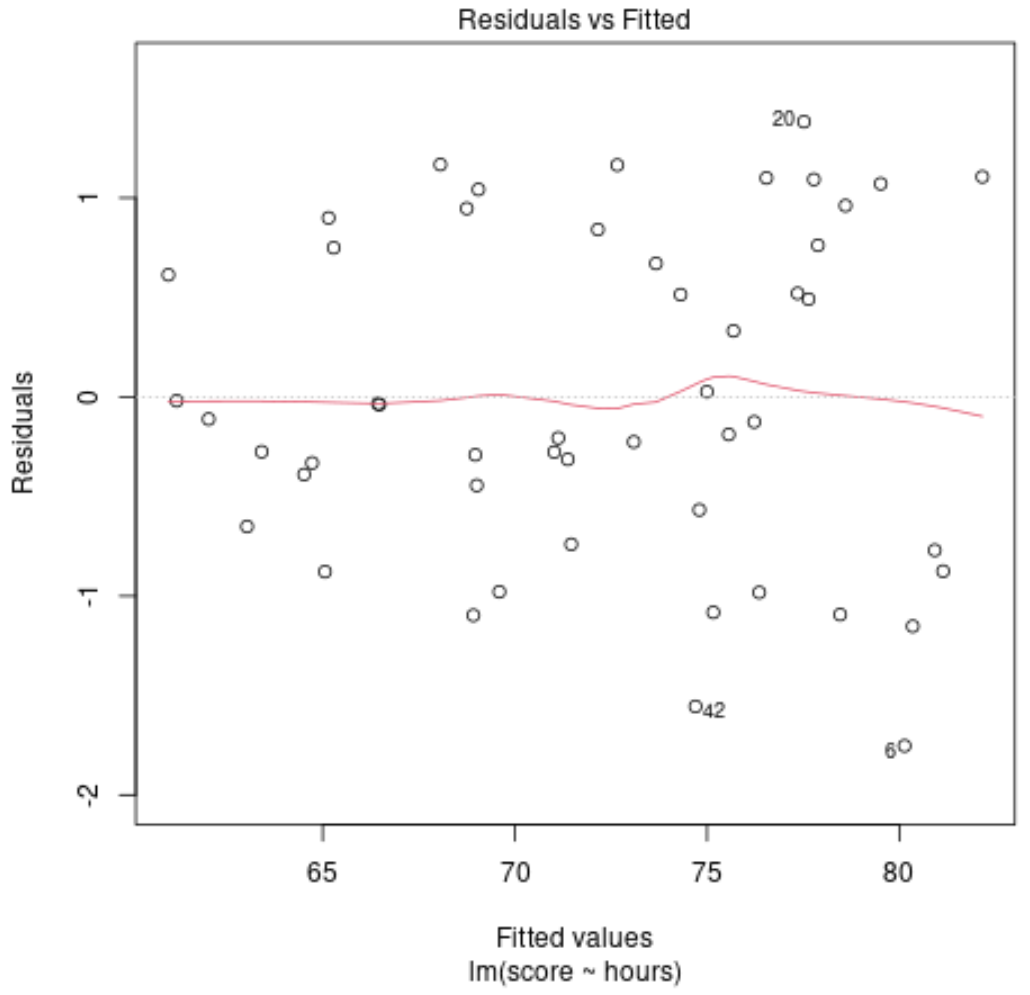
وتنتشر البقايا بشكل عشوائي حول الصفر بدون نمط واضح، مما يشير إلى أن النموذج الخطي يوفر ملاءمة مناسبة للبيانات.
ومع ذلك، لنفترض أن مخططنا للقيم المجهزة مقابل القيم المتبقية يبدو في الواقع كما يلي:
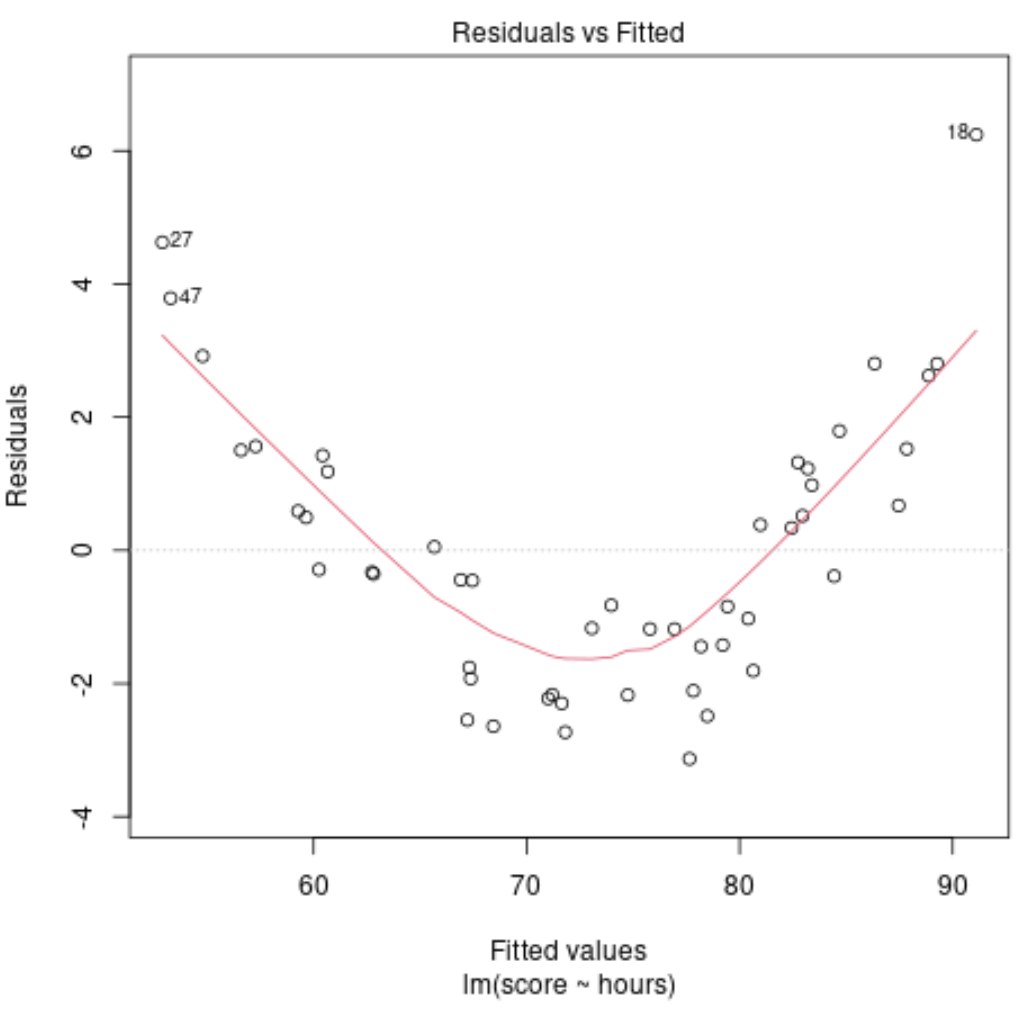
من الرسم البياني، يمكننا أن نرى أن هناك نمطًا غير خطي واضح في البقايا – تظهر البقايا على شكل “U”.
يخبرنا هذا أن النموذج الخطي غير مناسب لهذه البيانات المحددة وأنه قد يكون من الحكمة ملاءمة نموذج الانحدار متعدد الحدود بدلاً من ذلك.
3. احسب قيمة مربع R المعدلة للنموذج
هناك طريقة أخرى لتحديد ما إذا كان يجب عليك استخدام الانحدار متعدد الحدود وهي ملاءمة كل من نموذج الانحدار الخطي ونموذج الانحدار متعدد الحدود وحساب قيم R-squared المجهزة لكلا النموذجين.
يمثل مربع R المعدل نسبة التباين في متغير الاستجابة الذي يمكن تفسيره بواسطة متغيرات التوقع في النموذج، المعدل لعدد متغيرات التوقع في النموذج.
يمثل النموذج ذو أعلى مربع R معدل النموذج الأكثر قدرة على استخدام متغير (متغيرات) التوقع لشرح التباين في متغير الاستجابة.
مصادر إضافية
تشرح البرامج التعليمية التالية كيفية إجراء الانحدار متعدد الحدود باستخدام برامج إحصائية مختلفة:
مقدمة للانحدار متعدد الحدود
كيفية إجراء الانحدار متعدد الحدود في R
كيفية إجراء الانحدار متعدد الحدود في بايثون
كيفية تنفيذ الانحدار متعدد الحدود في إكسيل
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر