متى يتم استخدام انحدار ridge & lasso
في الانحدار الخطي المتعدد العادي، نستخدم مجموعة من متغيرات التوقع p ومتغير الاستجابة لتناسب نموذج النموذج:
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p
يتم اختيار قيم β 0 , β 1 , B 2 , …, β p باستخدام طريقة المربعات الصغرى التي تقلل مجموع مربعات البقايا (RSS):
RSS = Σ(y i – ŷ i ) 2
ذهب:
- Σ : رمز يعني “المجموع”
- y i : قيمة الاستجابة الفعلية للملاحظة رقم i
- ŷ i : قيمة الاستجابة المتوقعة للملاحظة i
مشكلة التعددية الخطية في الانحدار
المشكلة التي غالبًا ما تنشأ في الممارسة العملية مع الانحدار الخطي المتعدد هي التعددية الخطية – عندما يكون هناك ارتباط كبير بين متغيرين أو أكثر من متغيرات التنبؤ مع بعضها البعض، بحيث لا توفر معلومات فريدة أو مستقلة في نموذج الانحدار.
وهذا يمكن أن يجعل تقديرات معامل النموذج غير موثوقة وتظهر تباينًا كبيرًا. أي أنه عند تطبيق النموذج على مجموعة بيانات جديدة لم يسبق له رؤيتها من قبل، فمن المرجح أن يكون أداؤه ضعيفًا.
تجنب التعددية الخطية: انحدار ريدج ولاسو
هناك طريقتان يمكننا استخدامهما للتغلب على مشكلة الخطية المتعددة هذه، وهما انحدار التلال وانحدار اللاسو .
يسعى انحدار ريدج إلى تقليل ما يلي:
- آر إس إس + Σβ ي 2
يسعى انحدار Lasso إلى تقليل ما يلي:
- RSS + Σ|β ي |
وفي كلتا المعادلتين يسمى الحد الثاني عقوبة الانسحاب .
عندما تكون 0 = 0، فإن مصطلح العقوبة هذا ليس له أي تأثير وينتج انحدار التلال وانحدار اللاسو نفس تقديرات المعامل مثل المربعات الصغرى.
ومع ذلك، مع اقتراب π من اللانهاية، تصبح عقوبة الانكماش أكثر تأثيرًا وتتناقص المتغيرات التنبؤية غير القابلة للاستيراد في النموذج نحو الصفر.
مع انحدار لاسو، من الممكن أن تصبح بعض المعاملات صفرًا تمامًا عندما تصبح lect كبيرة بدرجة كافية.
مزايا وعيوب انحدار ريدج ولاسو
إن ميزة انحدار Ridge و Lasso على انحدار المربعات الصغرى هي مقايضة التحيز والتباين .
تذكر أن متوسط مربع الخطأ (MSE) هو مقياس يمكننا استخدامه لقياس دقة نموذج معين ويتم حسابه على النحو التالي:
MSE = فار( f̂( x 0 ) ) + [التحيز( f̂( x 0 )))] 2 + فار(ε)
MSE = التباين + الانحياز 2 + خطأ غير قابل للاختزال
الفكرة الأساسية لانحدار ريدج وانحدار لاسو هي تقديم انحياز صغير بحيث يمكن تقليل التباين بشكل كبير، مما يؤدي إلى انخفاض إجمالي المشروعات الصغيرة والمتوسطة.
لتوضيح ذلك، انظر إلى الرسم البياني التالي:
لاحظ أنه مع زيادة π، يتناقص التباين بشكل ملحوظ مع زيادة طفيفة جدًا في الانحياز. ومع ذلك، بعد نقطة معينة، يتناقص التباين بسرعة أقل ويؤدي انخفاض المعاملات إلى التقليل بشكل كبير من تقديرها، مما يؤدي إلى زيادة حادة في التحيز.
يمكننا أن نرى من الرسم البياني أن MSE للاختبار هو الأدنى عندما نختار قيمة π التي تنتج مفاضلة مثالية بين التحيز والتباين.
عندما تكون 0 = 0، فإن الحد الجزائي في انحدار اللاسو ليس له أي تأثير وبالتالي ينتج نفس تقديرات المعامل مثل المربعات الصغرى. ومع ذلك، من خلال زيادة π إلى نقطة معينة، يمكننا تقليل MSE الإجمالي للاختبار.
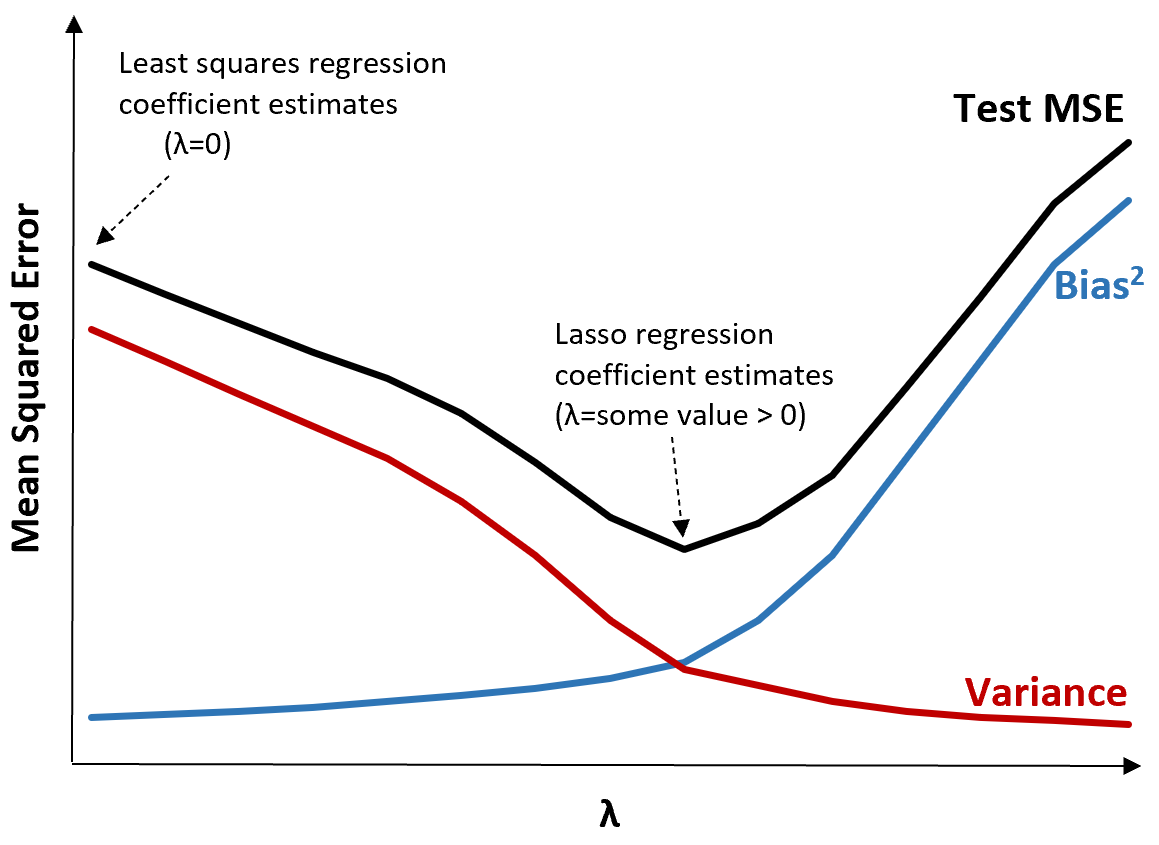
وهذا يعني أن ملاءمة النموذج عن طريق انحدار التلال واللاسو يمكن أن تنتج أخطاء اختبار أصغر من ملاءمة النموذج عن طريق انحدار المربعات الصغرى.
عيب انحدار Ridge و Lasso هو أنه يصبح من الصعب تفسير المعاملات في النموذج النهائي لأنها تتقلص نحو الصفر.
وبالتالي، يجب استخدام انحدار Ridge و Lasso عندما تريد تحسين القدرة التنبؤية بدلاً من الاستدلال.
ريدج ضد. انحدار لاسو: متى يجب استخدام كل منهما
يُعرف انحدار L asso وانحدار التلال بطرق التنظيم لأنهما يحاولان تقليل مجموع المربعات المتبقية (RSS) بالإضافة إلى مدة عقوبة معينة.
وبعبارة أخرى، فإنها تقيد أو تنظم تقديرات معاملات النموذج.
وهذا يثير السؤال بطبيعة الحال: هل انحدار التلال أم اللاسو أفضل؟
في الحالات التي يكون فيها عدد صغير فقط من متغيرات التوقع ذات أهمية، يميل انحدار اللاسو إلى العمل بشكل أفضل لأنه قادر على تقليل المتغيرات غير المهمة تمامًا إلى الصفر وإزالتها من النموذج.
ومع ذلك، عندما تكون العديد من المتغيرات المتوقعة مهمة في النموذج وتكون معاملاتها متساوية تقريبًا، يميل انحدار التلال إلى العمل بشكل أفضل لأنه يحافظ على جميع المتنبئين في النموذج.
لتحديد النموذج الأفضل للتنبؤات، نقوم عادةً بإجراء التحقق المتبادل من k-fold واختيار النموذج الذي ينتج أقل خطأ في جذر الاختبار لمتوسط مربع الخطأ.
مصادر إضافية
توفر البرامج التعليمية التالية مقدمة عن انحدار Ridge وانحدار Lasso:
تشرح البرامج التعليمية التالية كيفية تنفيذ كلا النوعين من الانحدار في R وPython:
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر