مخطط الشجرة
تشرح هذه المقالة ماهية المخطط الشجري وكيفية صنعه. وبالتالي، ستجد أمثلة على هياكل الأشجار، ومزايا هذا النوع من المخططات، بالإضافة إلى تمرين تم حله خطوة بخطوة.
ما هي الشجرة؟
المخطط الشجري ، والذي يُسمى أيضًا شجرة الاحتمالات ، هو تمثيل رسومي لجميع النتائج المحتملة للتجربة بالإضافة إلى احتمالاتها.
وبالتالي، يتم استخدام مخطط الشجرة البيانية لرسم جميع النتائج المحتملة في فضاء العينة وحساب احتمالاتها.
يتم عمل مخطط شجرة بحيث تتفرع كل نتيجة ( عقدة ) إلى نتائج محتملة جديدة ( فروع ) حتى يتم الوصول إلى النتائج النهائية.
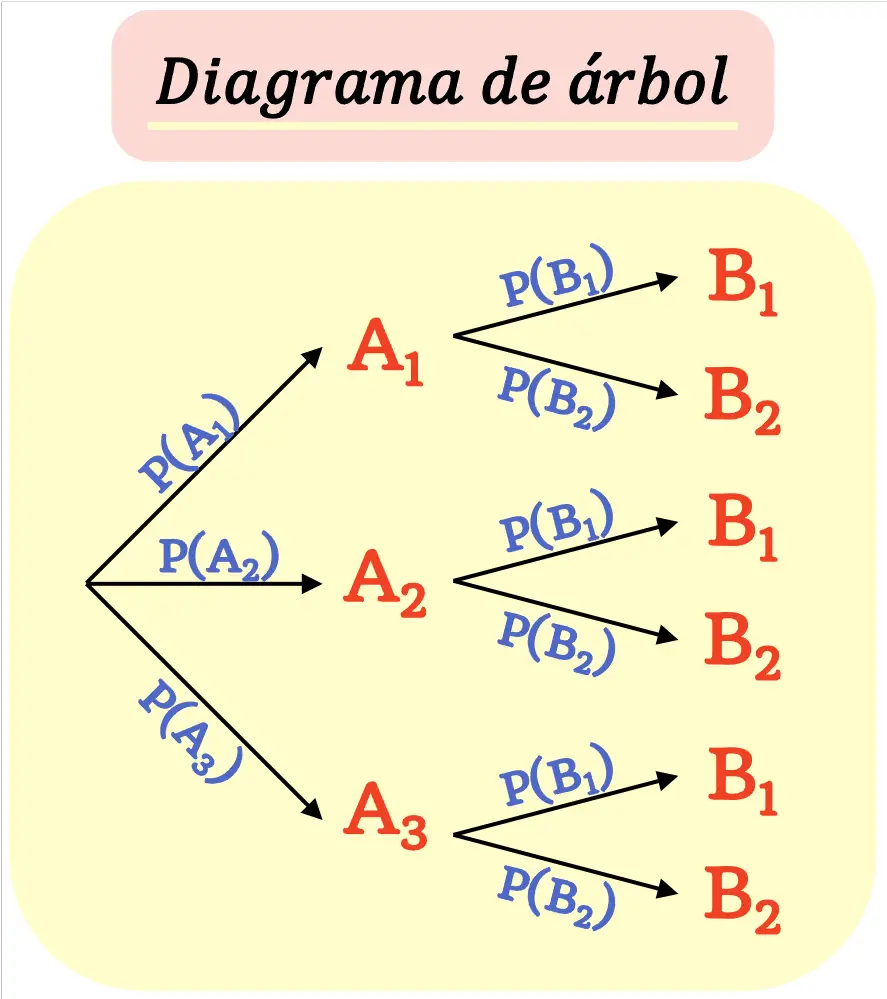
يجب أن يؤخذ في الاعتبار أن مجموع احتمالات جميع الفروع الخارجة من العقدة يجب أن يساوي 1.
كيفية عمل مخطط شجرة
لإنشاء شجرة، عليك اتباع الخطوات التالية:
- الخطوة الأولى في إنشاء مخطط الشجرة هي رسم فرع لكل نتيجة محتملة. وستكون هذه فروع الجيل الأول.
- ثم يتم إضافة الاحتمال المرتبط بكل حدث إلى الفرع المقابل له.
- نهاية كل فرع من فروع الجيل الأول هي العقدة التي يجب أن يتم من خلالها تمثيل فروع الأحداث المحتملة اللاحقة.
- كما في الفروع الأولى، يجب أن نضيف احتمالات الأحداث الممثلة.
- كرر الخطوتين 3 و4 حتى تصل إلى العقد النهائية، أي النهايات المحتملة للتجربة.
لاحظ أن عدد الفروع في مستوى واحد لا يجب بالضرورة أن يساوي عدد الفروع في مستوى مختلف. وبالمثل، فإن عدد الفروع التي تنتج عن نتيجة محتملة يمكن أن يختلف حتى داخل نفس المستوى.
مثال الشجرة
الآن بعد أن عرفنا تعريف ونظرية إنشاء مخطط شجرة، دعونا نلقي نظرة على مثال من العالم الحقيقي خطوة بخطوة لفهم المفهوم بشكل أفضل.
- أنشئ شجرة احتمالات رمي العملة لثلاث عملات مستقلة. ثم أوجد احتمالية الحصول على صورة في الرميات الثلاث.
عند إجراء القرعة، هناك نتيجتان محتملتان فقط، يمكننا الحصول على صورة أو كتابة. وبالتالي، فإن احتمال الحصول على صورة أو كتابة عند رمي قطعة نقود هو:
![]()
![]()
بمجرد أن نعرف احتمالات النتائج المحتملة، ننتقل إلى تمثيل المخطط الشجري.
نظرًا لأن رميات العملة مستقلة، فإن احتمال الحصول على صورة أو كتابة سيكون دائمًا هو نفسه لكل رمية. لذلك، لبناء الشجرة، يجب تمثيل فرعين (الرؤوس والذيول) بنفس الاحتمالية لكل رمية يتم إجراؤها.

وبمجرد أن نصنع الشجرة، كل ما علينا فعله هو تحديد احتمال رمي العملات الثلاث.
لحساب احتمالية النتيجة المحتملة لمخطط الشجرة البيانية، يجب ضرب احتمالات جميع الفروع المجاورة.
ولذلك، في هذه الحالة يجب علينا مضاعفة جميع احتمالات الحصول على الرؤوس، لأن هذه هي احتمالات المسار الذي يقودنا إلى النتيجة المرجوة.

وبالتالي، يتم حساب احتمال الحصول على صورة عند رميات العملات الثلاث على النحو التالي:
![]()
باختصار، احتمال الحصول على صورة ثلاث مرات متتالية هو 12.5%.
حل تمرين الشجرة
لا يوجد في القرية سوى 3 دور حضانة: 60% من الأطفال يذهبون إلى الحضانة “أ”، و30% إلى الحضانة “ب”، و10% إلى الحضانة “ج”. وبالإضافة إلى ذلك، في دور الحضانة الثلاث، 55% من السكان من الفتيات. قم ببناء الشجرة واحسب الاحتمالات التالية:
- احتمال أنه عند اختيار طفل عشوائيًا، يكون فتاة من الحضانة ب.
- احتمال أنه عند اختيار طفل عشوائياً من أي مركز رعاية نهارية، سيكون صبياً.
لاحظ أنه إذا كانت نسبة الفتيات في جميع دور الحضانة 55%، يتم حساب نسبة الأولاد ببساطة عن طريق طرح 1 ناقص 0.55:
![]()
الآن بعد أن عرفنا كل الاحتمالات، يمكننا إنشاء شجرة الاحتمالات بكل الاحتمالات:

وبذلك يتم حساب احتمال اختيار فتاة من الحضانة (ب) عشوائياً كما يلي:
![]()
من ناحية أخرى، لتحديد احتمال اختيار صبي في أي حضانة، يجب علينا أولاً إيجاد احتمالية اختيار صبي لكل حضانة، ثم جمعهما معًا:
![]()
![]()
![]()
![]()
مزايا هيكل الشجرة
ونظرًا لخصائص البنية الشجرية، فإن مزايا هذا النوع من الرسم البياني الإحصائي هي كما يلي:
- المخططات الشجرية مفيدة جدًا لاتخاذ القرارات.
- يمكن تمثيل العلاقة بين جميع النتائج المحتملة بيانيا.
- من السهل جدًا العثور على السبب الجذري للمشكلة.
- يسهل حل مسائل الاحتمالات والإحصائيات.
- يساعد المخطط الشجري في تنظيم الأفكار وتحليل الموقف.