مخطط دائري

في هذه المقالة، سوف تتعلم ما هو المخطط الدائري، وكيفية إنشاء مخطط دائري، وتمرين خطوة بخطوة لهذا النوع من المخططات. بالإضافة إلى ذلك، سوف تكون قادرًا على رؤية خصائص المخططات الدائرية.

ما هو الرسم البياني الدائري؟

المخطط الدائري ، ويسمى أيضًا المخطط الدائري ، هو نوع من المخططات الإحصائية المستخدمة لتمثيل النسب المئوية والنسب بشكل مرئي. وبشكل أكثر دقة، في المخطط الدائري، يتم تمثيل البيانات بأجزاء من الدائرة، بحيث تتناسب زاوية كل قطعة جبن مع ترددها.

ولذلك، كلما زاد تكرار القيمة، زادت الحصة التي تشغلها في المخطط الدائري.

في الإحصائيات، تعد المخططات الدائرية مفيدة جدًا لتمثيل البيانات النوعية على الرسم البياني، كما أنها تسمح لك باستخلاص النتائج بسرعة.

تجدر الإشارة إلى أن المخطط الدائري له العديد من الأسماء المختلفة مثل المخطط الدائري أو مخطط البيتزا أو المخطط الدائري أو مخطط الجبن أو حتى مخطط 360 درجة.

كيفية عمل مخطط دائري

بالنظر إلى تعريف المخطط الدائري، يوضح هذا القسم كيفية إنشاء مخطط من هذا النوع:

1. جمع البيانات الإحصائية وإعداد الجدول التكراري المناسب لها.
2. احسب زاوية كل قطاع من الرسم البياني باستخدام الصيغة التالية



ذهب



هي زاوية القطاع i ,



ترددها المطلق و



العدد الإجمالي للبيانات.

3. من الزوايا المحسوبة، قم بتمثيل القطاعات على رسم بياني دائري باستخدام المنقلة.
4. احسب النسبة المئوية لكل قطاع باستخدام الصيغة التالية:



ذهب



هي النسبة المئوية للقطاع i ،



ترددها المطلق و



العدد الإجمالي للبيانات.

5. وضح على الرسم البياني النسبة المئوية لكل قطاع.

مثال على الرسم البياني الدائري

لكي تتمكن من رؤية كيفية إنشاء المخطط الدائري، أترك لك مثالًا موضحًا خطوة بخطوة أدناه.

• تم سؤال 50 شخصًا عن مدينتهم المفضلة وتم تجميع البيانات في الجدول التالي. ارسم هذه البيانات الإحصائية على مخطط دائري.

عليك أولاً أن تجد الزاوية التي تتوافق مع كل قطعة جبن . للقيام بذلك، نطبق الصيغة التالية:

على سبيل المثال، يتم حساب الزاوية المقابلة للقيمة الأولى في جدول البيانات:

بمجرد معرفة الزاوية، قم ببساطة بتمثيل القطاع الدائري باستخدام المنقلة:

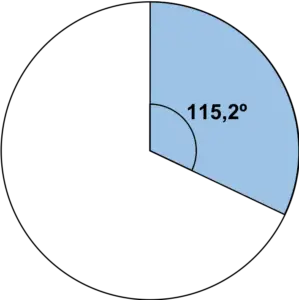
نكرر نفس الخطوة لجميع القيم الموجودة في الجدول:

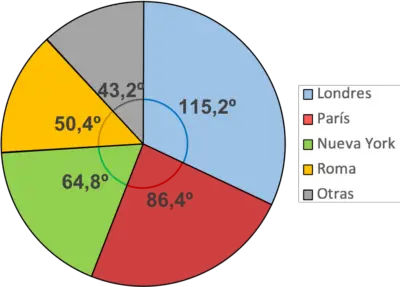
يوصى بتلوين كل قطاع بلون لتسهيل فهم الرسم البياني. وبالمثل، يجب عليك إضافة وسيلة إيضاح لإظهار معنى كل لون في الرسم التخطيطي.

بعد رسم الأجبان بيانيًا، نحتاج إلى حساب النسبة المئوية لكل منها لوضعها على الرسم البياني. للقيام بذلك، نستخدم الصيغة التالية:

وبالتالي فإن النسبة المئوية لكل قطاع هي:

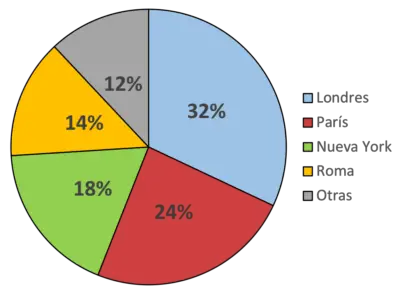
من خلال هذا المخطط الدائري نشير، على سبيل المثال، إلى أن اللون الأزرق يمثل مدينة لندن وهو المكان الذي يفضله معظم الناس (32% من الناس). ومن ناحية أخرى، يمثل اللون الأخضر مدينة نيويورك، وهي المدينة المفضلة لدى 18% ممن شملهم الاستطلاع.

ميزات الرسم البياني الدائري

خصائص كاممبرت هي كما يلي:

• يعد المخطط الدائري مفيدًا جدًا لتمثيل البيانات النوعية.
• ومع ذلك، هناك أنواع أخرى من الرسوم البيانية الإحصائية أكثر ملاءمة لتمثيل المتغيرات الكمية أو السلاسل الزمنية.
• بالإضافة إلى ذلك، يمكن تمثيل متغير واحد فقط في المخطط الدائري، مما يجعل من الصعب مقارنة المتغيرات.
• المخطط الدائري مرئي للغاية، مما يسمح بالتحليل والاستنتاجات السريعة.
• من الصعب قراءة الرسم البياني عندما يكون هناك العديد من القطاعات أو بعضها صغير جدًا. وفي مثل هذه الحالة، يوصى بتجميع القطاعات الصغيرة في قطاع واحد يسمى “أخرى”.