ما هو مستوى بيتا في الإحصاء؟ (التعريف & #038؛ مثال)
في الإحصاء، نستخدماختبار الفرضيات لتحديد ما إذا كانت الفرضية المتعلقة بمعلمة مجتمعية صحيحة.
يحتوي اختبار الفرضية دائمًا على الفرضيتين التاليتين:
الفرضية الصفرية (H 0 ): تتوافق بيانات العينة مع الاعتقاد السائد فيما يتعلق بمعلمة المجتمع.
الفرضية البديلة ( HA ): تشير بيانات العينة إلى أن الفرضية الواردة في الفرضية الصفرية غير صحيحة. بمعنى آخر، يؤثر السبب غير العشوائي على البيانات.
عندما نقوم بإجراء اختبار الفرضيات، هناك دائمًا أربع نتائج محتملة:
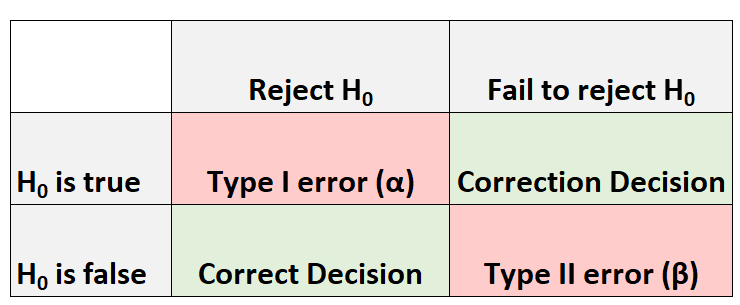
هناك نوعان من الأخطاء التي يمكن أن نرتكبها:
- الخطأ من النوع الأول: نرفض الفرضية الصفرية عندما تكون صحيحة بالفعل. يُشار إلى احتمال حدوث هذا النوع من الأخطاء بـ α .
- الخطأ من النوع الثاني: نفشل في رفض الفرضية الصفرية عندما تكون في الواقع خاطئة. ويلاحظ احتمال حدوث هذا النوع من الخطأ β .
العلاقة بين ألفا وبيتا
من الناحية المثالية، يريد الباحثون أن يكون احتمال ارتكاب خطأ من النوع الأول واحتمال ارتكاب خطأ من النوع الثاني منخفضًا.
ومع ذلك، هناك حل وسط بين هذين الاحتمالين. إذا قمنا بتقليل مستوى ألفا، فقد نقلل من احتمال رفض الفرضية الصفرية عندما تكون صحيحة بالفعل، ولكن هذا يزيد في الواقع من مستوى بيتا – احتمال فشلنا في رفض الفرضية الصفرية عندما تكون خاطئة.
العلاقة بين القوة وبيتا
تشير قوة اختبار الفرضية إلى احتمال اكتشاف تأثير أو اختلاف عندما يكون التأثير أو الاختلاف موجودًا بالفعل. وبعبارة أخرى، هو احتمال رفض الفرضية الصفرية الخاطئة بشكل صحيح.
يتم حسابه على النحو التالي:
الطاقة = 1 – β
بشكل عام، يريد الباحثون أن تكون قوة الاختبار عالية بحيث إذا كان هناك تأثير أو اختلاف يستطيع الاختبار اكتشافه.
من المعادلة أعلاه، يمكننا أن نرى أن أفضل طريقة لزيادة قوة الاختبار هي تقليل مستوى بيتا. وأفضل طريقة لتقليل مستوى البيتا هي عادةً زيادة حجم العينة.
توضح الأمثلة التالية كيفية حساب مستوى بيتا لاختبار الفرضية وتوضح لماذا يمكن أن تؤدي زيادة حجم العينة إلى تقليل مستوى بيتا.
مثال 1: حساب بيتا لاختبار الفرضية
لنفترض أن أحد الباحثين يريد اختبار ما إذا كان متوسط وزن الأدوات المصغّرة المنتجة في المصنع أقل من 500 أونصة. نحن نعلم أن الانحراف المعياري للأوزان هو 24 أوقية ويقرر الباحث جمع عينة عشوائية مكونة من 40 قطعة.
سوف تحقق الفرضية التالية عند α = 0.05:
- ح 0 : μ = 500
- ح أ : μ <500
تخيل الآن أن متوسط وزن الأدوات المصغّرة هو في الواقع 490 أونصة. بمعنى آخر، يجب رفض الفرضية الصفرية.
يمكننا استخدام الخطوات التالية لحساب مستوى بيتا – احتمال عدم رفض الفرضية الصفرية في حين أنه ينبغي في الواقع رفضها:
الخطوة 1: ابحث عن منطقة عدم الرفض.
وفقًا لآلة حاسبة قيمة Z الحرجة، فإن القيمة الحرجة اليسرى عند α = 0.05 هي -1.645 .
الخطوة 2: ابحث عن الحد الأدنى من العينة التي سنفشل في رفضها.
يتم حساب إحصائية الاختبار كـ z = ( x – μ) / (s/ √n )
وبذلك يمكننا حل هذه المعادلة لمتوسط العينة:
- س = μ – ض*(ق/ √ن )
- س = 500 – 1.645*(24/ √40 )
- س = 493.758
الخطوة 3: تحديد احتمال حدوث الحد الأدنى لمتوسط العينة بالفعل.
يمكننا حساب هذا الاحتمال على النحو التالي:
- ف(ض ≥ (493.758 – 490) / (24/√ 40 ))
- ف (ض ≥ 0.99)
وفقًا لآلة حاسبة CDF العادية ، فإن احتمال Z ≥ 0.99 هو 0.1611 .
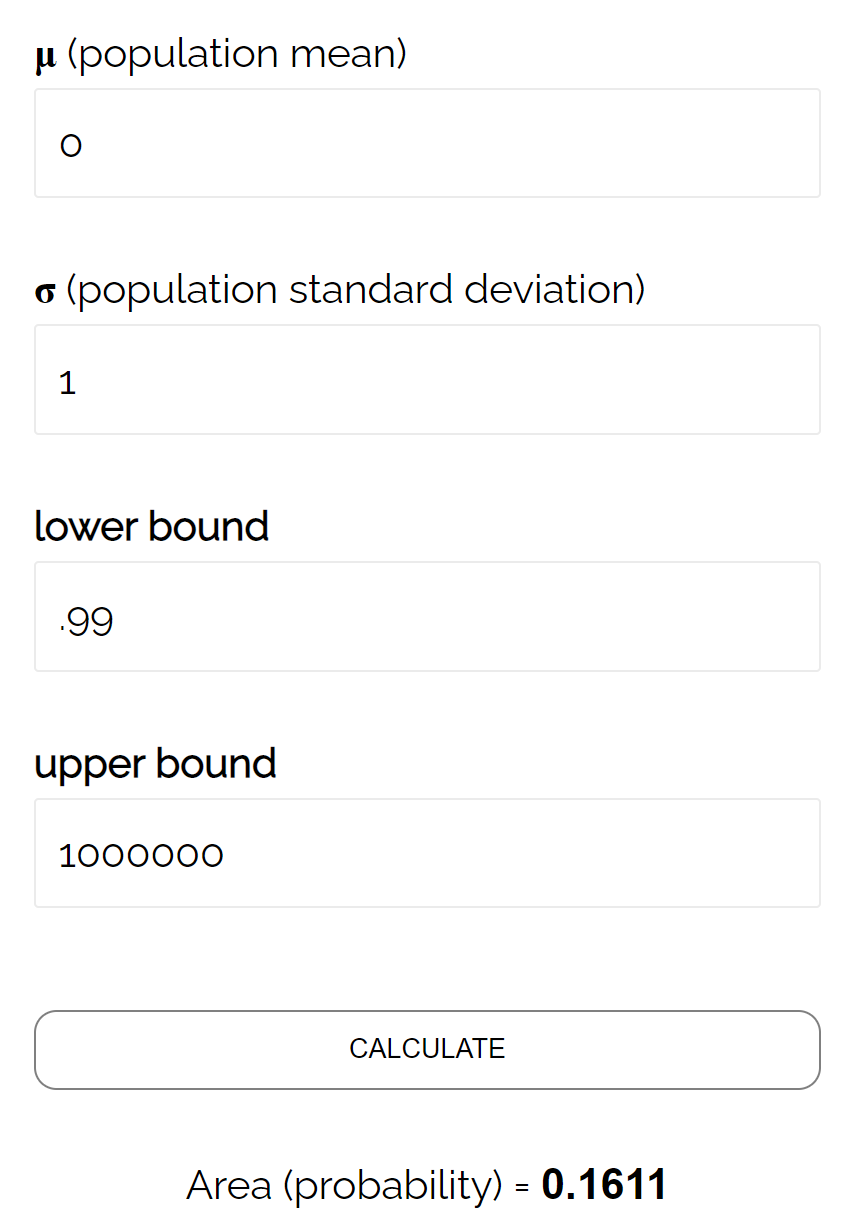
وبالتالي، فإن مستوى بيتا لهذا الاختبار هو β = 0.1611. وهذا يعني أن هناك فرصة بنسبة 16.11% لعدم اكتشاف الفرق إذا كان المتوسط الفعلي 490 أونصة.
المثال 2: حساب بيتا لاختبار بحجم عينة أكبر
لنفترض الآن أن الباحث يقوم بإجراء نفس اختبار الفرضية بالضبط، ولكنه بدلاً من ذلك يستخدم عينة من عناصر واجهة المستخدم = n = 100. يمكننا تكرار نفس الخطوات الثلاث لحساب مستوى البيتا لهذا الاختبار:
الخطوة 1: ابحث عن منطقة عدم الرفض.
وفقًا لآلة حاسبة قيمة Z الحرجة، فإن القيمة الحرجة اليسرى عند α = 0.05 هي -1.645 .
الخطوة 2: ابحث عن الحد الأدنى من العينة التي سنفشل في رفضها.
يتم حساب إحصائية الاختبار كـ z = ( x – μ) / (s/ √n )
وبذلك يمكننا حل هذه المعادلة لمتوسط العينة:
- س = μ – ض*(ق/ √ن )
- س = 500 – 1.645*(24/√ 100 )
- س = 496.05
الخطوة 3: تحديد احتمال حدوث الحد الأدنى لمتوسط العينة بالفعل.
يمكننا حساب هذا الاحتمال على النحو التالي:
- ف(ض ≥ (496.05 – 490) / (24/√ 100 ))
- ف (ض ≥ 2.52)
وفقًا لآلة حاسبة CDF العادية ، فإن احتمال Z ≥ 2.52 هو 0.0059.
وبالتالي، فإن مستوى بيتا لهذا الاختبار هو β = 0.0059. وهذا يعني أن هناك فرصة بنسبة 0.59% فقط لعدم اكتشاف الفرق إذا كان المتوسط الفعلي هو 490 أونصة.
لاحظ أنه بمجرد زيادة حجم العينة من 40 إلى 100، تمكن الباحث من تقليل مستوى بيتا من 0.1611 إلى 0.0059.
المكافأة: استخدم حاسبة الأخطاء من النوع الثاني لحساب المستوى التجريبي للاختبار تلقائيًا.
مصادر إضافية
مقدمة لاختبار الفرضيات
كيفية كتابة فرضية العدم (5 أمثلة)
شرح القيم P والأهمية الإحصائية