كيفية إنشاء وتفسير مصفوفة الارتباط في excel

إحدى الطرق لقياس العلاقة بين متغيرين هي استخدام معامل ارتباط بيرسون ، وهو مقياس للارتباط الخطي بين متغيرين .

لها قيمة بين -1 و 1 حيث:

• يشير -1 إلى وجود علاقة خطية سلبية تمامًا بين متغيرين
• يشير 0 إلى عدم وجود علاقة خطية بين متغيرين
• يشير الشكل 1 إلى وجود علاقة خطية إيجابية تمامًا بين متغيرين

وكلما زاد معامل الارتباط عن الصفر، كلما كانت العلاقة بين المتغيرين أقوى.

لكن في بعض الحالات، نريد أن نفهم العلاقة بين أزواج متعددة من المتغيرات.

في هذه الحالات، يمكننا إنشاء مصفوفة ارتباط ، وهي عبارة عن جدول مربع يوضح معاملات الارتباط بين عدة مجموعات زوجية من المتغيرات.

يشرح هذا البرنامج التعليمي كيفية إنشاء وتفسير مصفوفة الارتباط في Excel.

كيفية إنشاء مصفوفة الارتباط في إكسل

لنفترض أن لدينا مجموعة البيانات التالية التي توضح متوسط عدد النقاط والمرتدات والتمريرات الحاسمة لـ 10 من لاعبي كرة السلة:

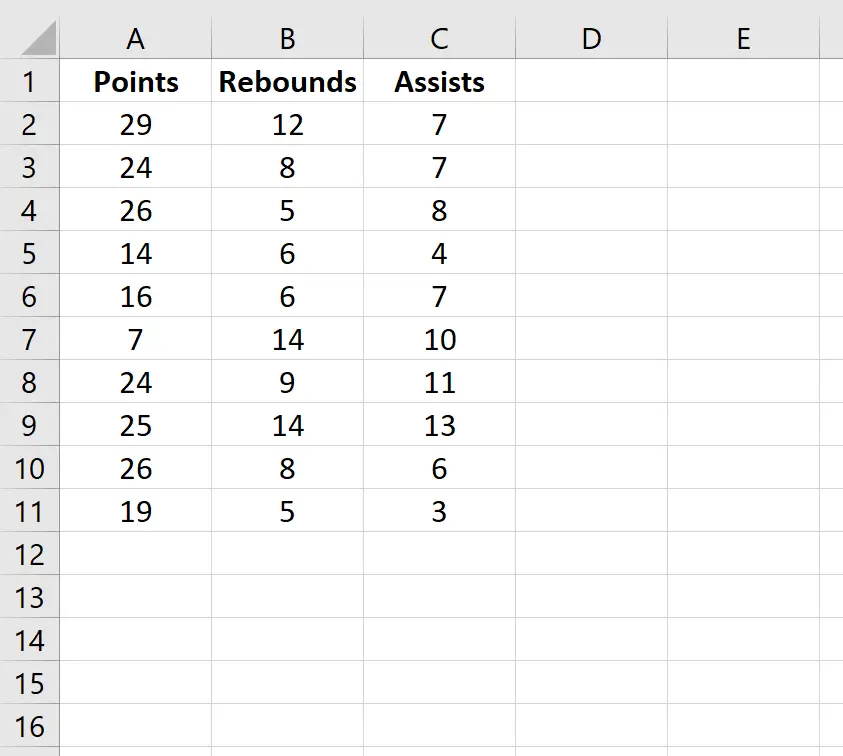
لإنشاء مصفوفة ارتباط لمجموعة البيانات هذه، انتقل إلى علامة التبويب “البيانات” في الشريط العلوي لبرنامج Excel وانقر فوق “تحليل البيانات” .

إذا لم تتمكن من رؤية هذا الخيار، فيجب عليك أولاً تحميل حزمة أدوات تحليل البيانات المجانية في Excel .

في النافذة الجديدة التي تظهر، حدد الارتباط ثم انقر فوق موافق .

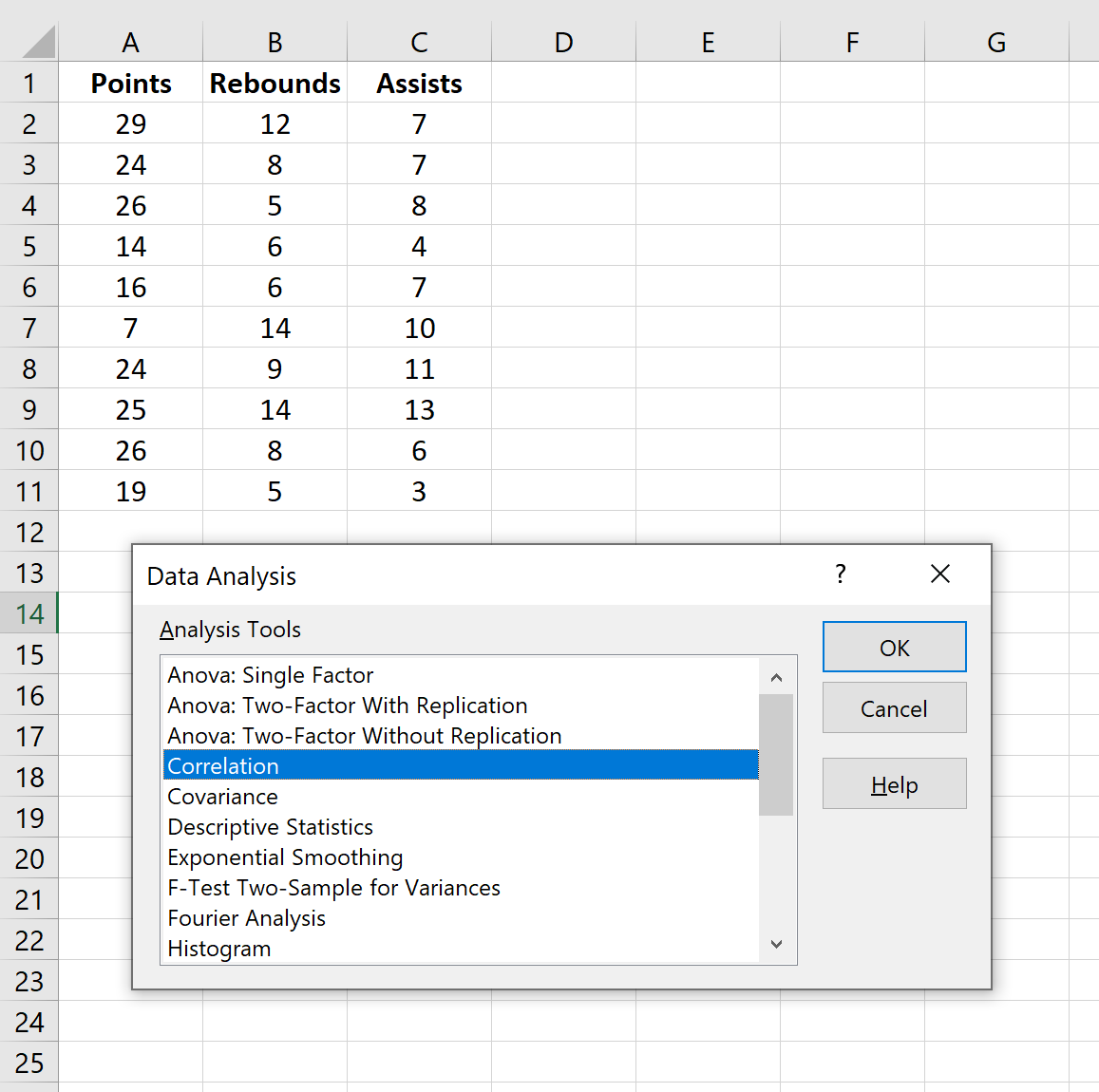
بالنسبة لنطاق الإدخال ، حدد الخلايا التي توجد بها البيانات (بما في ذلك الصف الأول الذي يحتوي على تسميات). حدد المربع بجوار التسميات في الصف الأول . بالنسبة لنطاق الإخراج ، حدد الخلية التي تريد أن تظهر فيها مصفوفة الارتباط. ثم انقر فوق موافق .

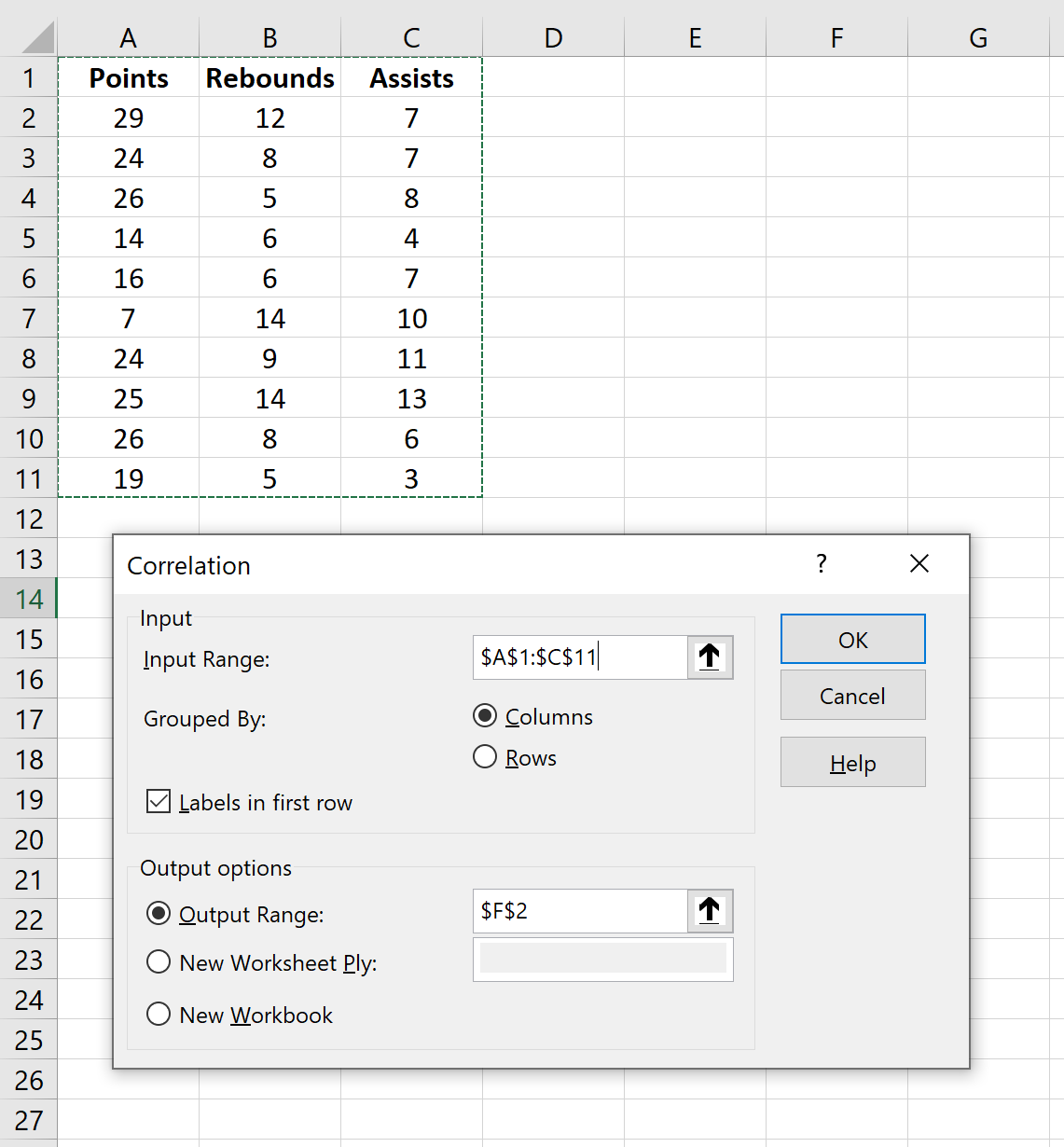
سيؤدي هذا تلقائيًا إلى إنتاج مصفوفة الارتباط التالية:

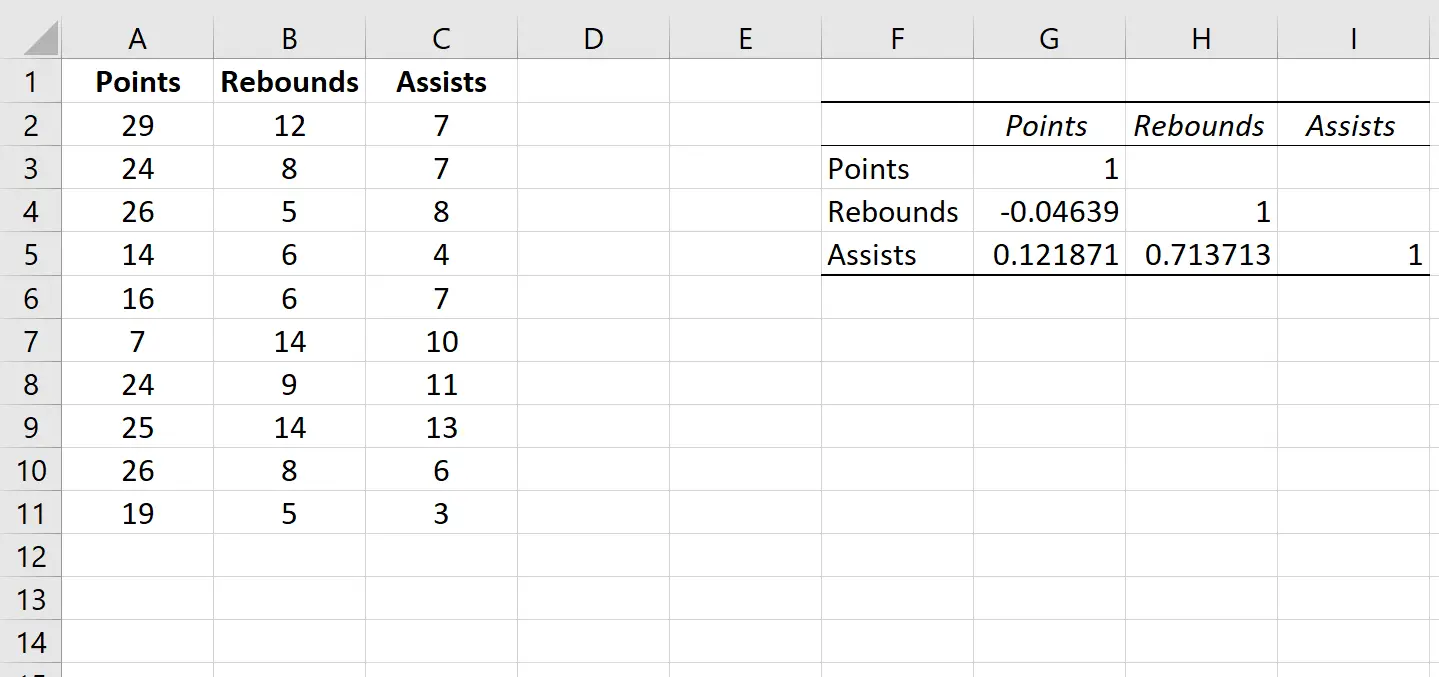
كيفية تفسير مصفوفة الارتباط في إكسيل

تخبرنا القيم الموجودة في الخلايا الفردية لمصفوفة الارتباط بمعامل ارتباط بيرسون بين كل مجموعة زوجية من المتغيرات. على سبيل المثال:

الارتباط بين النقاط والمرتدات: -0.04639. ترتبط النقاط والمرتدات بشكل سلبي قليلاً، ولكن هذه القيمة قريبة جدًا من الصفر بحيث لا يوجد دليل قوي على وجود ارتباط كبير بين هذين المتغيرين.

الارتباط بين النقاط والتمريرات الحاسمة: 0.121871. ترتبط النقاط والتمريرات بشكل إيجابي قليلاً، ولكن هذه القيمة أيضًا قريبة جدًا من الصفر، لذلك لا يوجد دليل قوي على وجود ارتباط كبير بين هذين المتغيرين.

الارتباط بين المرتدات والتمريرات الحاسمة: 0.713713. ترتبط الكرات المرتدة والتمريرات الحاسمة بشكل إيجابي قوي. وهذا يعني أن اللاعبين الذين لديهم المزيد من الكرات المرتدة يميلون أيضًا إلى الحصول على المزيد من التمريرات الحاسمة.

لاحظ أن القيم القطرية لمصفوفة الارتباط كلها 1 لأن الارتباط بين المتغير ونفسه هو دائمًا 1. عمليًا، هذا الرقم ليس مفيدًا في التفسير.

المكافأة: تصور معاملات الارتباط

هناك طريقة بسيطة لتصور قيمة معاملات الارتباط في الجدول وهي تطبيق التنسيق الشرطي على الجدول.

في الشريط العلوي لبرنامج Excel، انتقل إلى علامة التبويب الصفحة الرئيسية ، ثم مجموعة الأنماط .

انقر فوق مخطط التنسيق الشرطي ، ثم مقاييس الألوان ، ثم مقياس الألوان الأخضر والأصفر والأحمر .

يؤدي هذا تلقائيًا إلى تطبيق مقياس الألوان التالي على مصفوفة الارتباط:

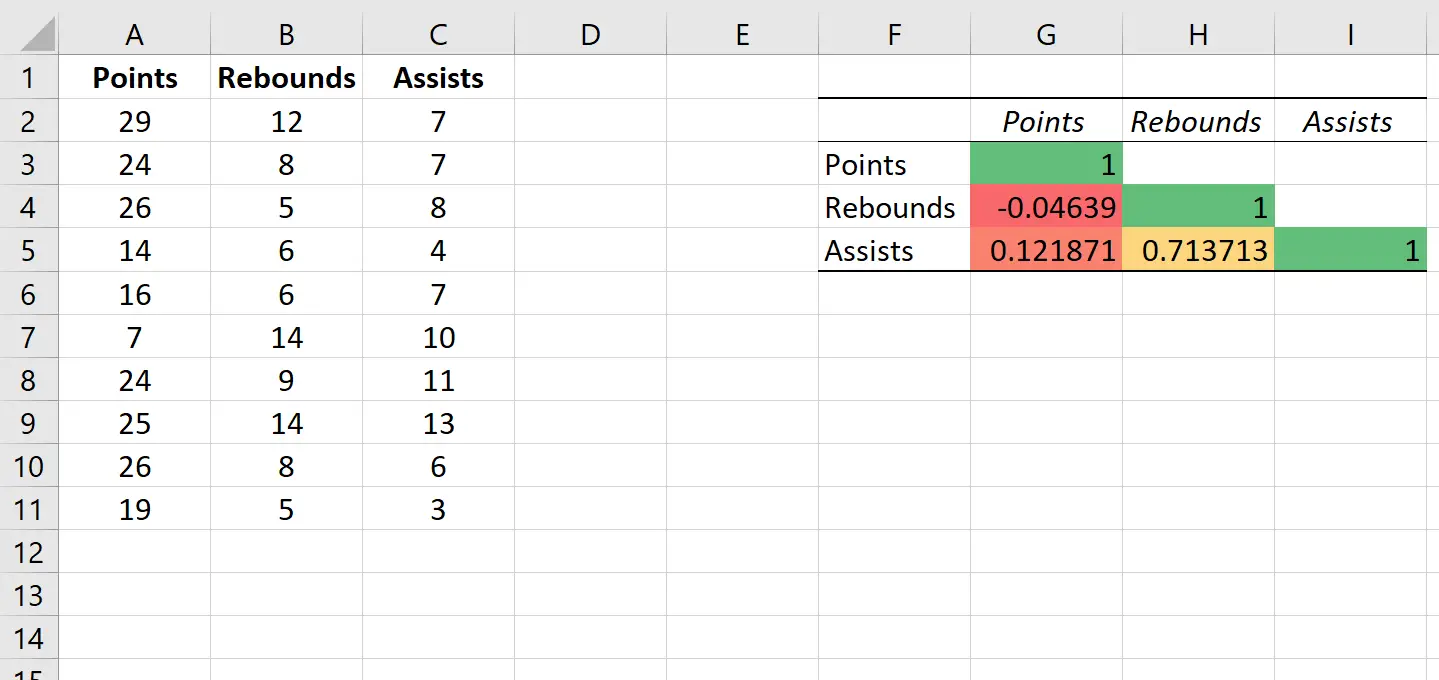
وهذا يساعدنا على تصور قوة الارتباطات بين المتغيرات بسهولة.

هذه نصيحة مفيدة بشكل خاص إذا كنا نعمل مع مصفوفة ارتباط تحتوي على العديد من المتغيرات، لأنها تساعدنا على التعرف بسرعة على المتغيرات التي لديها أقوى الارتباطات.

ذات صلة: ما الذي يعتبر ارتباطًا “قويًا”؟

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى في R:

كيفية إنشاء مصفوفة مخطط التشتت في إكسل
كيفية إجراء اختبار الارتباط في إكسيل