كيفية إنشاء مصفوفة الارتباط في جداول بيانات جوجل

إحدى الطرق لقياس العلاقة بين متغيرين هي استخدام معامل ارتباط بيرسون ، وهو مقياس للارتباط الخطي بين متغيرين . لها قيمة بين -1 و 1 حيث:

• يشير -1 إلى وجود علاقة خطية سلبية تمامًا بين متغيرين
• يشير 0 إلى عدم وجود علاقة خطية بين متغيرين
• يشير الشكل 1 إلى وجود علاقة خطية إيجابية تمامًا بين متغيرين

وكلما زاد معامل الارتباط عن الصفر، كلما كانت العلاقة بين المتغيرين أقوى.

لكن في بعض الحالات، نريد أن نفهم العلاقة بين أزواج متعددة من المتغيرات. في هذه الحالات، يمكننا إنشاء مصفوفة ارتباط ، وهي عبارة عن جدول مربع يوضح معاملات الارتباط بين عدة مجموعات زوجية من المتغيرات.

يشرح هذا البرنامج التعليمي كيفية إنشاء وتفسير مصفوفة الارتباط في جداول بيانات Google.

كيفية إنشاء مصفوفة الارتباط في جداول بيانات جوجل

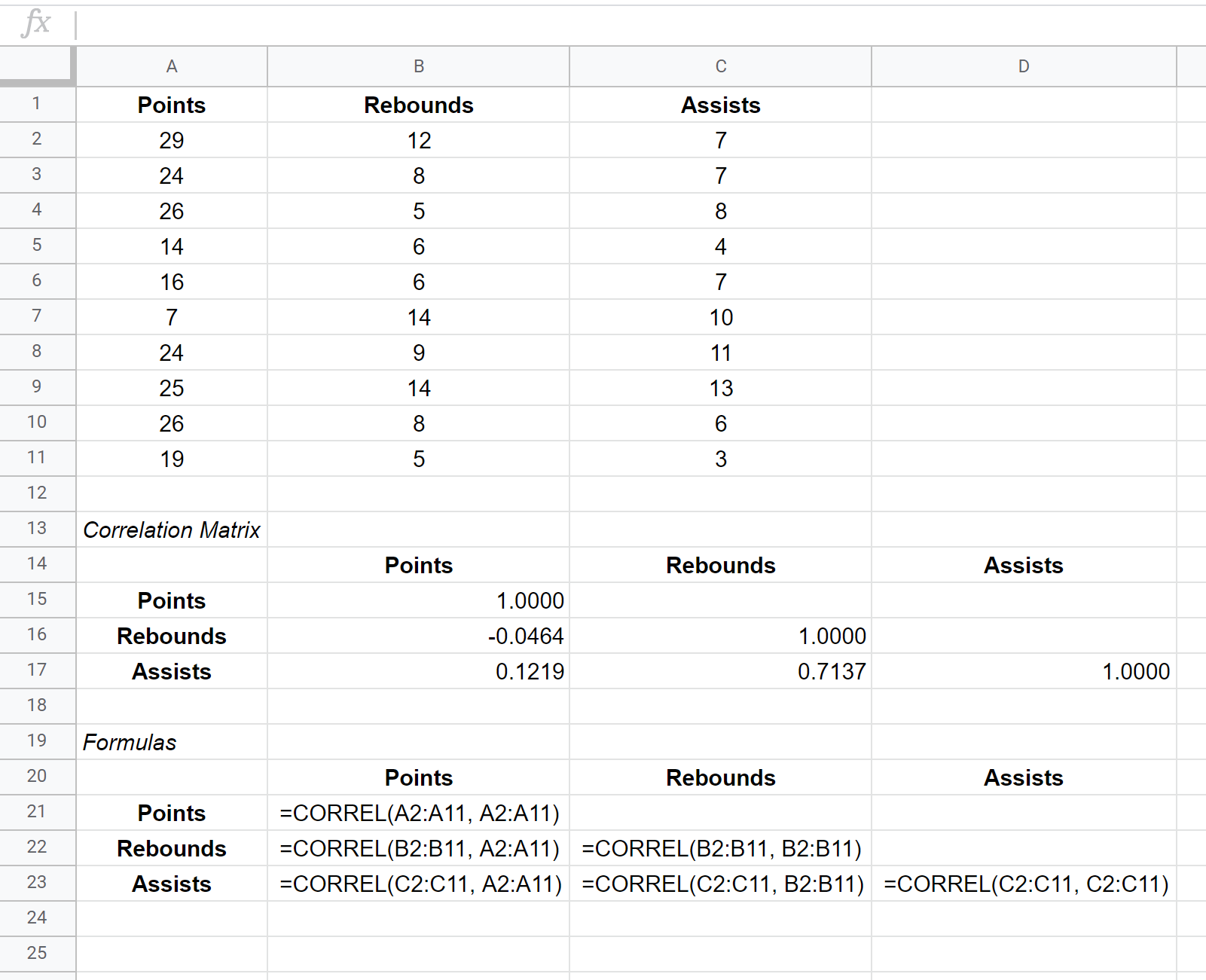
لنفترض أن لدينا مجموعة البيانات التالية التي توضح متوسط عدد النقاط والمرتدات والتمريرات الحاسمة لـ 10 من لاعبي كرة السلة:

لإنشاء مصفوفة ارتباط لمجموعة البيانات هذه، يمكننا استخدام الدالة CORREL() بالصيغة التالية:

  COVAR(data_y، data_x)

تظهر مصفوفة التباين المشترك لمجموعة البيانات هذه في الخلايا B15:D17 بينما تظهر الصيغ المستخدمة لإنشاء مصفوفة التباين المشترك في الخلايا B21:D23 أدناه:

كيفية تفسير مصفوفة الارتباط

تخبرنا القيم الموجودة في الخلايا الفردية لمصفوفة الارتباط بمعامل ارتباط بيرسون بين كل مجموعة زوجية من المتغيرات. على سبيل المثال:

الارتباط بين النقاط والمرتدات: -0.0464. ترتبط النقاط والمرتدات بشكل سلبي قليلاً، ولكن هذه القيمة قريبة جدًا من الصفر بحيث لا يوجد دليل قوي على وجود ارتباط كبير بين هذين المتغيرين.

الارتباط بين النقاط والتمريرات الحاسمة: 0.1219. ترتبط النقاط والتمريرات بشكل إيجابي قليلاً، ولكن هذه القيمة أيضًا قريبة جدًا من الصفر، لذلك لا يوجد دليل قوي على وجود ارتباط كبير بين هذين المتغيرين.

الارتباط بين المرتدات والتمريرات الحاسمة: 0.7137. ترتبط الكرات المرتدة والتمريرات الحاسمة بشكل إيجابي قوي. وهذا يعني أن اللاعبين الذين لديهم المزيد من الكرات المرتدة يميلون أيضًا إلى الحصول على المزيد من التمريرات الحاسمة.

لاحظ أن القيم القطرية لمصفوفة الارتباط كلها 1 لأن الارتباط بين المتغير ونفسه هو دائمًا 1. عمليًا، هذا الرقم ليس مفيدًا في التفسير.

مصادر إضافية

كيفية قراءة مصفوفة الارتباط
كيفية إنشاء مصفوفة الارتباط في إكسل