كيفية إنشاء مصفوفة التباين في برنامج spss

التباين هو مقياس لكيفية ارتباط التغييرات في متغير واحد بالتغيرات في المتغير الثاني. وبشكل أكثر تحديدًا، فهو مقياس لدرجة ارتباط متغيرين خطيًا.

صيغة حساب التباين بين متغيرين X و Y هي:

COV( X , Y ) = Σ(x- x )(y- y ) / n

مصفوفة التغاير هي مصفوفة مربعة توضح التباين بين المتغيرات المختلفة في مجموعة البيانات.

يشرح هذا البرنامج التعليمي كيفية إنشاء مصفوفة التغاير لمجموعة بيانات معينة في برنامج SPSS.

مثال: مصفوفة التغاير في برنامج SPSS

لنفترض أن لدينا مجموعة البيانات التالية التي توضح درجات اختبار 10 طلاب مختلفين في ثلاث مواد: الرياضيات والعلوم والتاريخ:

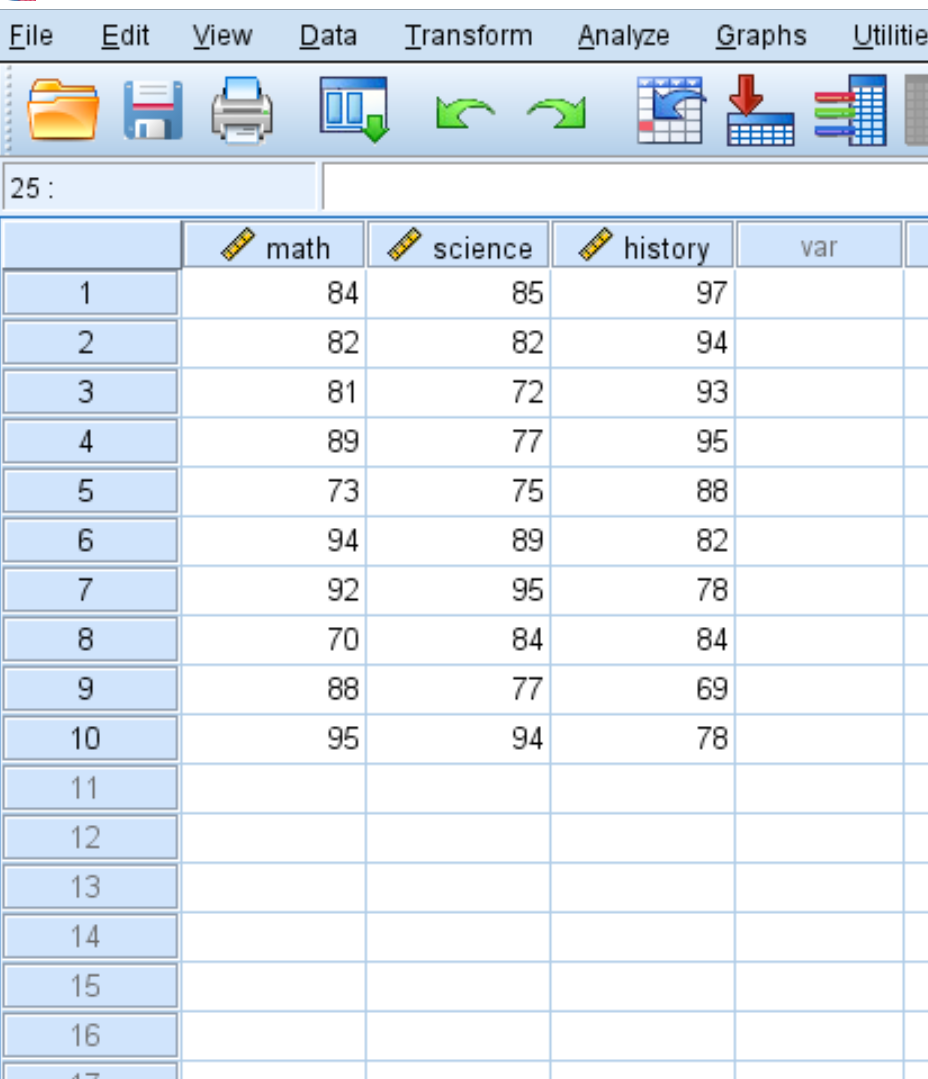
لإنشاء مصفوفة التغاير لمجموعة البيانات هذه، انقر فوق علامة التبويب تحليل ، ثم ربط ، ثم ثنائي المتغير :

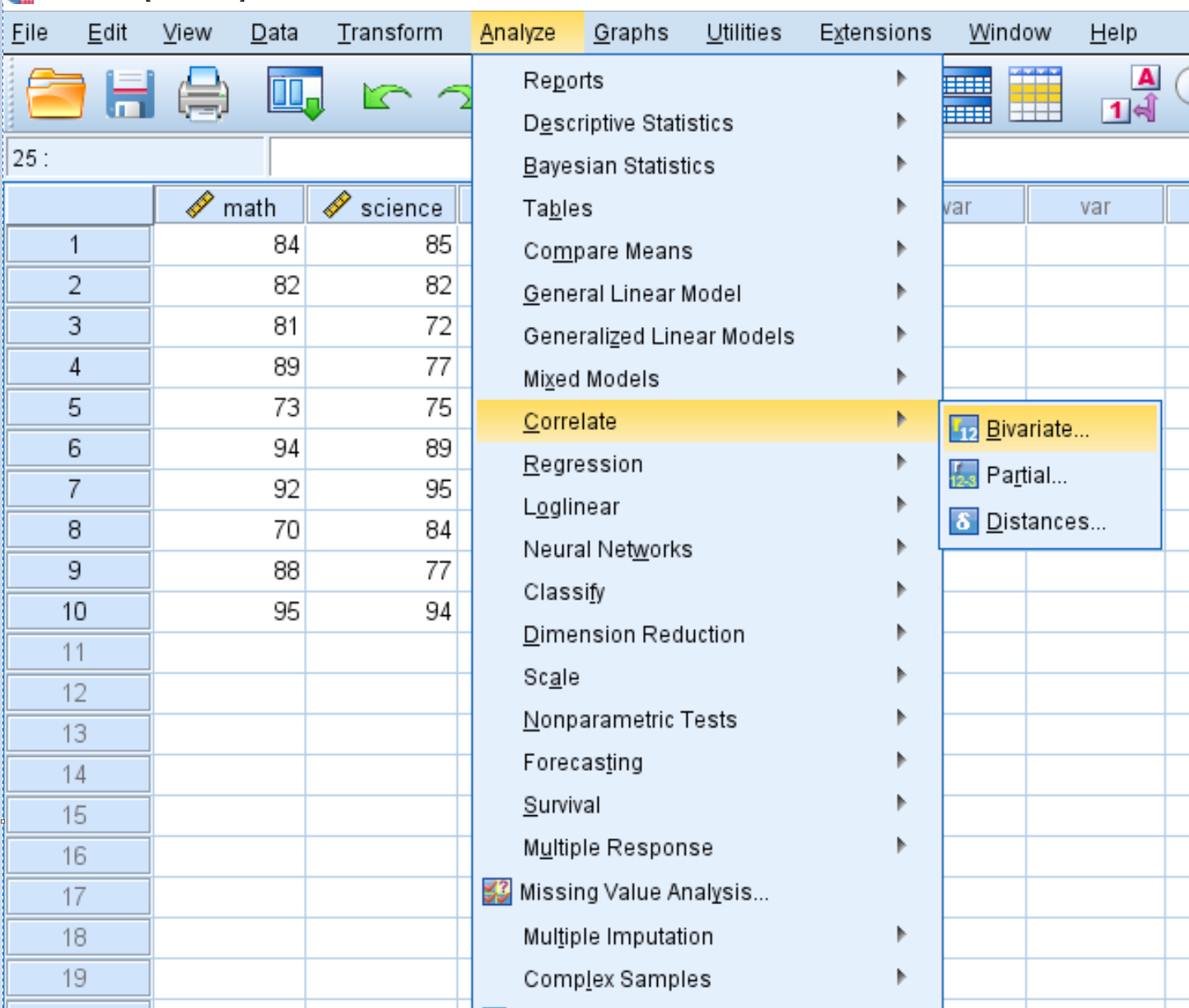
في النافذة الجديدة التي تظهر، اسحب كل متغير من المتغيرات الثلاثة إلى المربع المسمى المتغيرات :

بعد ذلك، انقر فوق خيارات . حدد المربع بجوار التباينات والتباينات بين المنتجات . ثم انقر فوق “متابعة” .

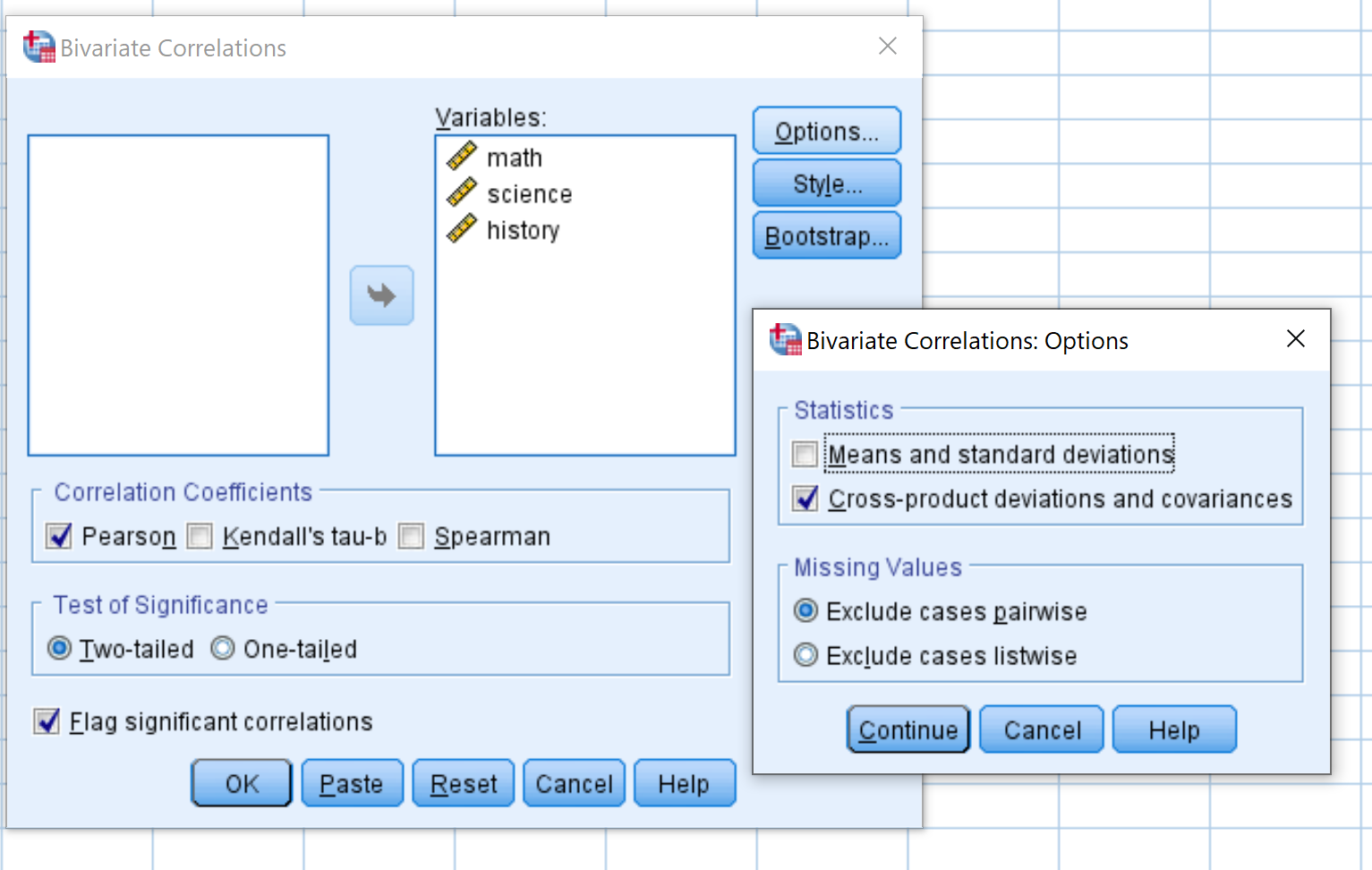
ثم انقر فوق موافق . ستظهر النتيجة في نافذة جديدة:

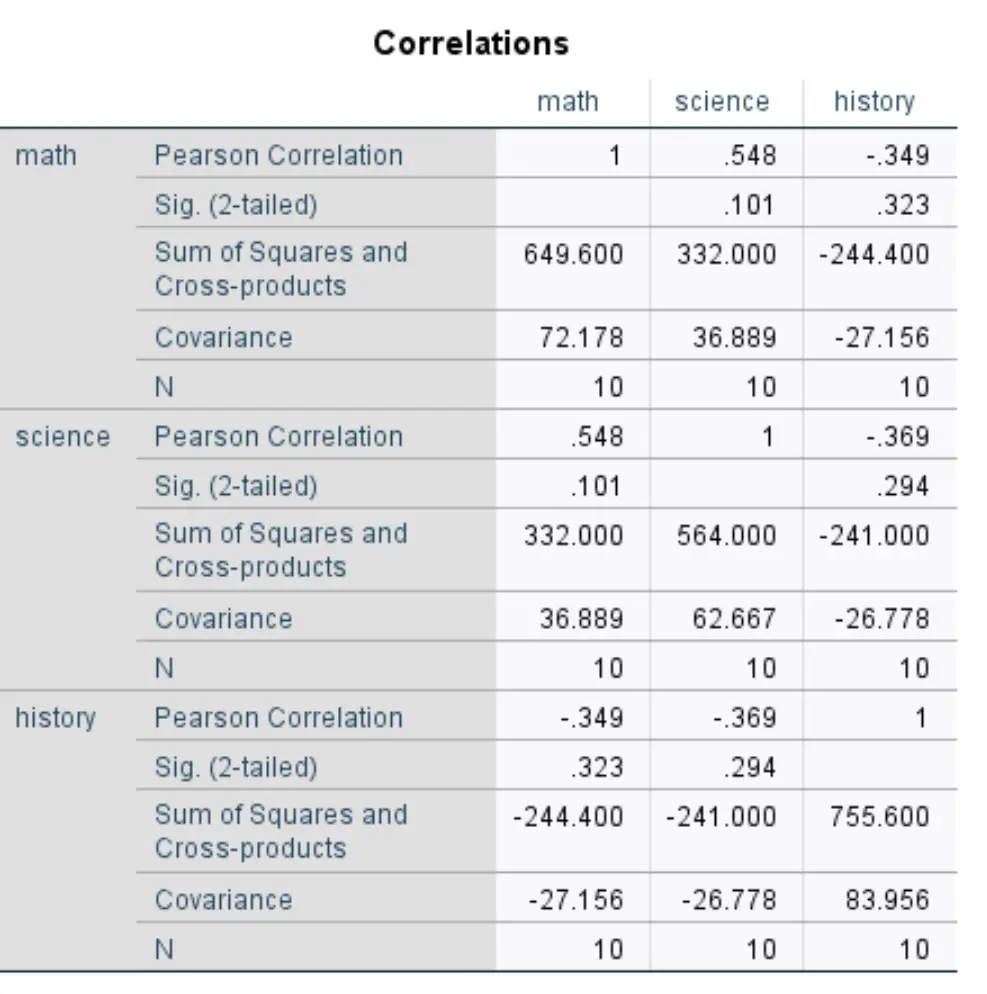
للحصول على التباين لكل مجموعة زوجية من المتغيرات، تحتاج إلى قسمة مجموع المربعات ومنتجات المتجهات على N.

على سبيل المثال، يمكن حساب التباين بين الرياضيات والعلوم على النحو التالي:

COV (الرياضيات والعلوم) = 332,000 / 10 = 33.2 .

وبالمثل، يمكن حساب التباين بين الرياضيات والتاريخ على النحو التالي:

COV (الرياضيات والتاريخ) = -244.400 / 10 = -24.44 .

يمكنك أيضًا الحصول على التباين لكل متغير عن طريق قسمة مجموع المربعات ومنتجات المتجهات على N.

على سبيل المثال، يمكن حساب التباين في الرياضيات على النحو التالي:

VAR(رياضيات) = 649.600 / 10 = 64.96 .

يمكنك الحصول على مصفوفة التغاير الكاملة لمجموعة البيانات هذه عن طريق إجراء حسابات مماثلة:

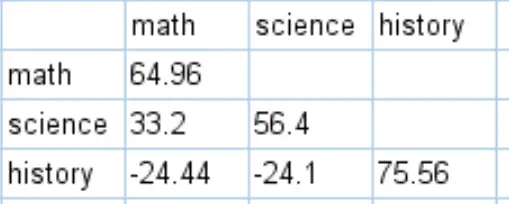
كيفية تفسير مصفوفة التغاير

القيم على طول أقطار مصفوفة التغاير هي ببساطة تباينات كل موضوع. على سبيل المثال:

• التباين في نتائج الرياضيات هو 64.96 .
• التباين في درجات العلوم هو 56.4 .
• التباين في الدرجات التاريخية هو 75.56 .

تمثل القيم الأخرى للمصفوفة التباينات بين المواضيع المختلفة. على سبيل المثال:

• التباين بين درجات الرياضيات والعلوم هو 33.2 .
• التباين بين درجات الرياضيات والتاريخ هو -24.44 .
• التباين بين درجات العلوم والتاريخ هو -24.1 .

يشير الرقم الموجب للتباين المشترك إلى أن متغيرين يميلان إلى الزيادة أو النقصان بالترادف. على سبيل المثال، يوجد تباين مشترك إيجابي في الرياضيات والعلوم (33.2)، مما يشير إلى أن الطلاب الذين يحصلون على درجات عالية في الرياضيات يميلون أيضًا إلى الحصول على درجات عالية في العلوم. وبالمثل، فإن الطلاب الذين يكون أداؤهم ضعيفًا في الرياضيات يميلون أيضًا إلى الأداء الضعيف في العلوم.

يشير الرقم السالب للتباين المشترك إلى أنه مع زيادة متغير واحد، يميل المتغير الثاني إلى الانخفاض. على سبيل المثال، يوجد تباين مشترك سلبي بين العلوم والتاريخ (-24.1)، مما يشير إلى أن الطلاب الذين يحصلون على درجات عالية في العلوم يميلون إلى الحصول على درجات منخفضة في التاريخ. وبالمثل، فإن الطلاب الذين يحصلون على درجات منخفضة في العلوم يميلون إلى الحصول على درجات عالية في التاريخ.

مصادر إضافية

كيفية إنشاء مصفوفة الارتباط في SPSS
كيفية حساب الارتباط الجزئي في برنامج SPSS