كيفية إنشاء مصفوفة التغاير في بايثون

التباين هو مقياس لكيفية ارتباط التغييرات في متغير واحد بالتغيرات في المتغير الثاني. وبشكل أكثر تحديدًا، فهو مقياس لدرجة ارتباط متغيرين خطيًا.

مصفوفة التغاير هي مصفوفة مربعة توضح التباين بين العديد من المتغيرات المختلفة. يمكن أن تكون هذه طريقة مفيدة لفهم كيفية ارتباط المتغيرات المختلفة في مجموعة البيانات.

يوضح المثال التالي كيفية إنشاء مصفوفة التغاير في بايثون.

كيفية إنشاء مصفوفة التغاير في بايثون

استخدم الخطوات التالية لإنشاء مصفوفة التغاير في بايثون.

الخطوة 1: إنشاء مجموعة البيانات.

أولاً، سنقوم بإنشاء مجموعة بيانات تحتوي على درجات اختبار 10 طلاب مختلفين في ثلاث مواد: الرياضيات والعلوم والتاريخ.

 import numpy as np

math = [84, 82, 81, 89, 73, 94, 92, 70, 88, 95]
science = [85, 82, 72, 77, 75, 89, 95, 84, 77, 94]
history = [97, 94, 93, 95, 88, 82, 78, 84, 69, 78]

data = np.array([math, science, history])

الخطوة 2: إنشاء مصفوفة التغاير.

بعد ذلك، سنقوم بإنشاء مصفوفة التباين المشترك لمجموعة البيانات هذه باستخدام الدالة numpy cov() ، مع تحديد هذا التحيز = True حتى نتمكن من حساب مصفوفة التباين المشترك السكاني.

 np.cov(data, bias= True )

array([[ 64.96, 33.2, -24.44],
       [33.2, 56.4, -24.1],
       [-24.44, -24.1, 75.56]])

الخطوة 3: تفسير مصفوفة التغاير.

القيم على طول أقطار المصفوفة هي ببساطة الفروق في كل موضوع. على سبيل المثال:

• التباين في درجات الرياضيات هو 64.96
• التباين في درجات العلوم هو 56.4
• التباين التاريخي في النتيجة هو 75.56

تمثل القيم الأخرى للمصفوفة التباينات بين المواضيع المختلفة. على سبيل المثال:

• التباين بين درجات الرياضيات والعلوم هو 33.2.
• التباين بين درجات الرياضيات والتاريخ هو -24.44.
• التباين بين درجات العلوم والتاريخ هو -24.1.

يشير الرقم الموجب للتباين المشترك إلى أن متغيرين يميلان إلى الزيادة أو النقصان بالترادف. على سبيل المثال، يوجد تباين مشترك إيجابي في الرياضيات والعلوم (33.2)، مما يشير إلى أن الطلاب الذين يحصلون على درجات عالية في الرياضيات يميلون أيضًا إلى الحصول على درجات عالية في العلوم. وعلى العكس من ذلك، فإن الطلاب الذين يكون أداؤهم ضعيفًا في الرياضيات يميلون أيضًا إلى الأداء الضعيف في العلوم.

يشير الرقم السالب للتباين المشترك إلى أنه مع زيادة متغير واحد، يميل المتغير الثاني إلى الانخفاض. على سبيل المثال، يوجد تباين مشترك سلبي في الرياضيات والتاريخ (-24.44)، مما يشير إلى أن الطلاب الذين يحصلون على درجات عالية في الرياضيات يميلون إلى الحصول على درجات منخفضة في التاريخ. وعلى العكس من ذلك، فإن الطلاب الذين يحصلون على درجات منخفضة في الرياضيات يميلون إلى الحصول على درجات عالية في التاريخ.

الخطوة 4: تصور مصفوفة التغاير (اختياري).

يمكنك تصور مصفوفة التغاير باستخدام وظيفة Heatmap() لحزمة Seaborn:

 import seaborn as sns
import matplotlib.pyplot as plt

cov = np.cov(data, bias=True)
labs = ['math', 'science', 'history']

sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs)
plt.show()

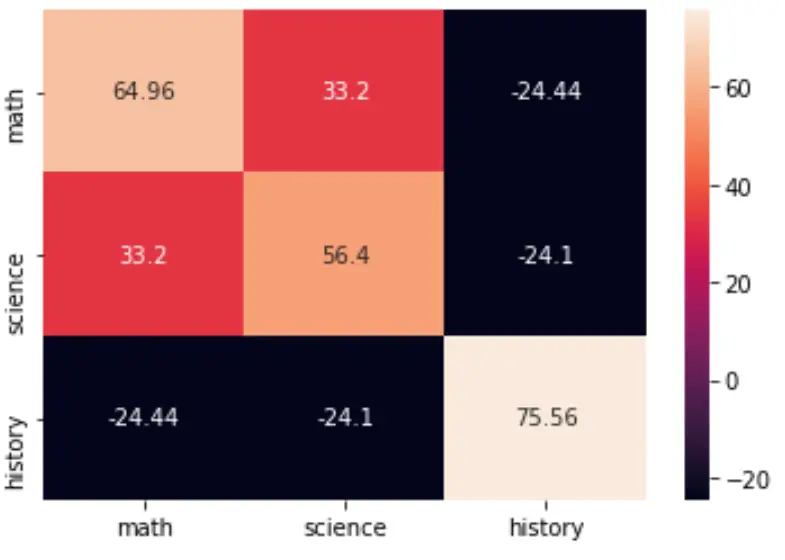
يمكنك أيضًا تغيير لوحة الألوان عن طريق تحديد الوسيطة cmap :

 sns.heatmap(cov, annot=True, fmt='g', xticklabels=labs, yticklabels=labs, cmap=' YlGnBu ')
plt.show() 

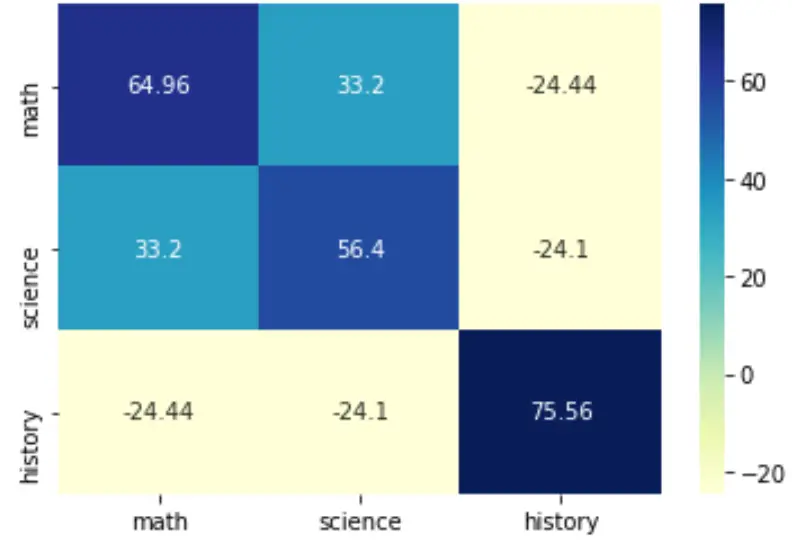
لمزيد من التفاصيل حول كيفية تصميم هذه الخريطة الحرارية، راجع وثائق seaborn .