معامل ارتباط بيرسون

معامل ارتباط بيرسون (المعروف أيضًا باسم “معامل الارتباط بين المنتج واللحظة”) هو مقياس للارتباط الخطي بين متغيرين X و Y. وله قيمة تتراوح بين -1 و1 حيث:

• يشير -1 إلى وجود علاقة خطية سلبية تمامًا بين متغيرين
• يشير 0 إلى عدم وجود علاقة خطية بين متغيرين
• يشير الشكل 1 إلى وجود علاقة خطية إيجابية تمامًا بين متغيرين

صيغة إيجاد معامل ارتباط بيرسون

صيغة إيجاد معامل ارتباط بيرسون، المشار إليها بـ r ، لعينة من البيانات هي ( عبر ويكيبيديا ):

ربما لن تضطر أبدًا إلى حساب هذه الصيغة يدويًا حيث يمكنك استخدام برنامج للقيام بذلك نيابةً عنك، ولكن من المفيد أن تفهم ما تفعله هذه الصيغة بالضبط من خلال الاطلاع على أحد الأمثلة.

لنفترض أن لدينا مجموعة البيانات التالية:

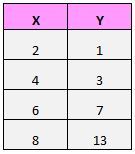
إذا قمنا برسم هذه الأزواج (X، Y) على مخطط التشتت، فسيبدو الأمر كما يلي:

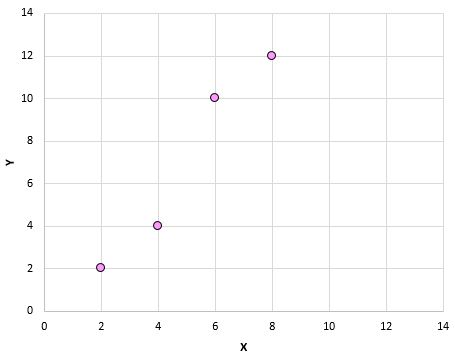
بمجرد النظر إلى مخطط التشتت هذا، يمكننا أن نرى أن هناك ارتباطًا إيجابيًا بين المتغيرين X وY: مع زيادة X، يميل Y إلى الزيادة أيضًا. ولكن لتحديد مدى الارتباط الإيجابي بين هذين المتغيرين، نحتاج إلى إيجاد معامل ارتباط بيرسون.

دعونا نركز فقط على بسط الصيغة:

بالنسبة لكل زوج (X، Y) في مجموعة البيانات الخاصة بنا، نحتاج إلى إيجاد الفرق بين قيمة x ومتوسط قيمة x، والفرق بين قيمة y ومتوسط قيمة y، ثم ضرب هذين الرقمين معًا.

على سبيل المثال، الزوج الأول (X، Y) هو (2، 2). متوسط قيمة x في مجموعة البيانات هذه هو 5 ومتوسط قيمة y في مجموعة البيانات هذه هو 7. لذا فإن الفرق بين قيمة x لهذا الزوج ومتوسط قيمة x هو 2 – 5 = -3. الفرق بين قيمة y لهذا الزوج ومتوسط قيمة y هو 2 – 7 = -5. ثم عندما نضرب هذين الرقمين نحصل على -3 * -5 = 15.

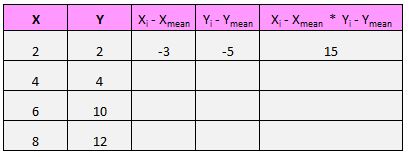
فيما يلي نظرة عامة مرئية على ما فعلناه للتو:

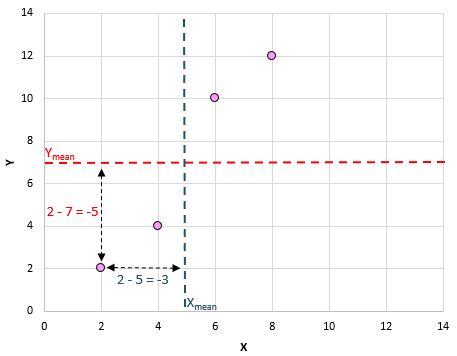
ثم قم بذلك لكل زوج:

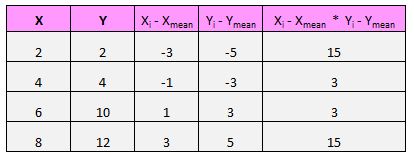
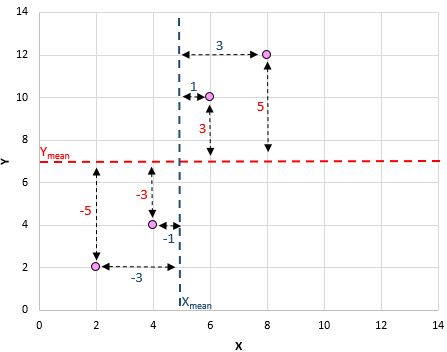
الخطوة الأخيرة للحصول على بسط الصيغة هي ببساطة إضافة كل هذه القيم معًا:

15 + 3 +3 + 15 = 36

ثم يطلب منا مقام الصيغة إيجاد مجموع جميع الفروق التربيعية لـ x وy، ثم ضرب هذين الرقمين معًا، ثم أخذ الجذر التربيعي:

لذا، أولًا، سنوجد مجموع مربعات الاختلافات بين x وy:

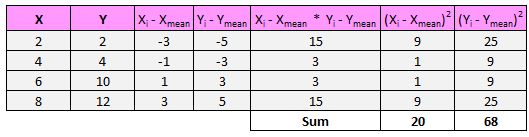
بعد ذلك، سنضرب هذين الرقمين معًا: 20 * 68 = 1,360.

وأخيرًا، سنأخذ الجذر التربيعي: √ 1,360 = 36.88

إذن وجدنا أن بسط الصيغة هو 36 ومقامها 36.88. وهذا يعني أن معامل ارتباط بيرسون لدينا هو r = 36 / 36.88 = 0.976

هذا الرقم قريب من 1، مما يشير إلى وجود علاقة خطية إيجابية قوية بين المتغيرين X و Y. وهذا يؤكد العلاقة التي لاحظناها في مخطط التشتت.

عرض الارتباطات

تذكر أن معامل ارتباط بيرسون يخبرنا بنوع العلاقة الخطية (إيجابية، سلبية، لا شيء) بين متغيرين وكذلك قوة هذه العلاقة (ضعيفة، متوسطة، قوية).

عندما نقوم بإنشاء مخطط تشتت لمتغيرين، يمكننا أن نرى العلاقة الحقيقية بين متغيرين. فيما يلي الأنواع العديدة من العلاقات الخطية التي قد نلاحظها:

علاقة قوية وإيجابية: كلما زاد المتغير على المحور السيني، زاد المتغير على المحور الصادي أيضًا. النقاط متجمعة بشكل وثيق، مما يدل على وجود علاقة قوية.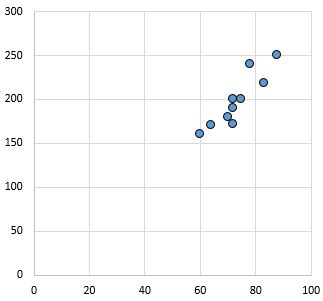

معامل ارتباط بيرسون: 0.94

العلاقة الضعيفة والموجبة: كلما زاد المتغير على المحور x، زاد المتغير على المحور y أيضًا. النقاط متناثرة تماما، مما يدل على ضعف العلاقة.

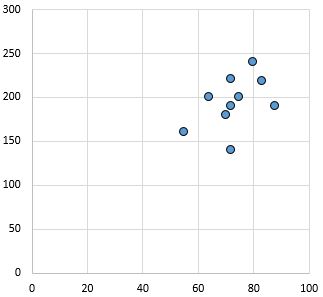
معامل ارتباط بيرسون: 0.44

لا توجد علاقة: لا توجد علاقة واضحة (إيجابية أو سلبية) بين المتغيرات.

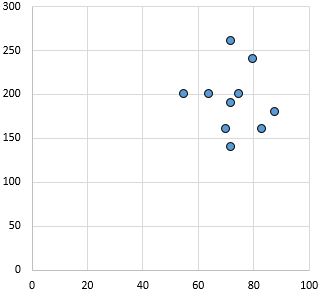
معامل ارتباط بيرسون: 0.03

علاقة قوية سلبية: كلما زاد المتغير على المحور x، انخفض المتغير على المحور y. النقاط مترابطة بإحكام، مما يدل على وجود علاقة قوية.

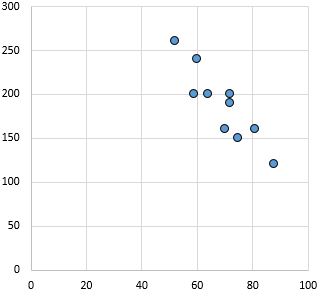
معامل ارتباط بيرسون: -0.87

العلاقة الضعيفة والسلبية: كلما زاد المتغير على المحور x، انخفض المتغير على المحور y. النقاط متناثرة تماما، مما يدل على ضعف العلاقة.

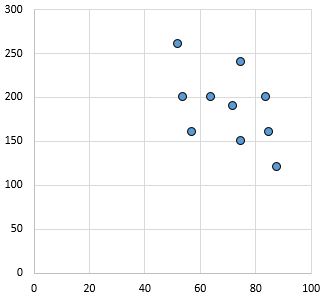
معامل ارتباط بيرسون: – 0.46

اختبار أهمية معامل ارتباط بيرسون

عندما نجد معامل ارتباط بيرسون لمجموعة من البيانات، فإننا غالبًا ما نعمل مع عينة من البيانات من مجموعة أكبر من السكان . وهذا يعني أنه من الممكن إيجاد علاقة غير صفرية لمتغيرين حتى لو لم يكونا مرتبطين فعليًا في إجمالي عدد السكان.

على سبيل المثال، لنفترض أننا أنشأنا مخططًا مبعثرًا للمتغيرين X و Y لكل نقطة بيانات في المجتمع بأكمله ويبدو كما يلي:

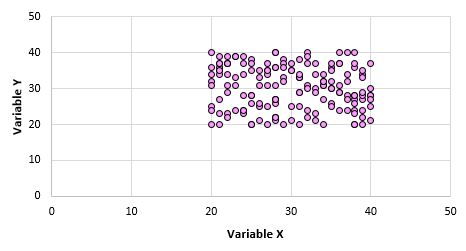
ومن الواضح أن هذين المتغيرين غير مرتبطين. لكن من الممكن عندما نأخذ عينة مكونة من 10 نقاط من المجتمع أن نختار النقاط التالية:

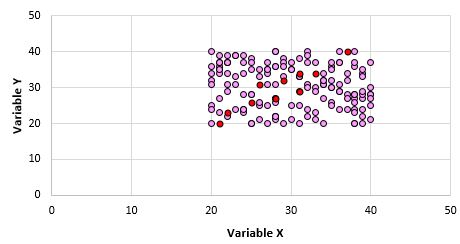
يمكننا أن نرى أن معامل ارتباط بيرسون لهذه العينة من النقاط هو 0.93، مما يشير إلى وجود ارتباط إيجابي قوي على الرغم من أن الارتباط السكاني هو صفر.

ومن أجل اختبار ما إذا كان الارتباط بين متغيرين ذو دلالة إحصائية أم لا، يمكننا إيجاد إحصائية الاختبار التالية:

إحصائية الاختبار T = r * √ (n-2) / (1-r ² )

حيث n هو عدد الأزواج في العينة، وr هو معامل ارتباط بيرسون، وتتبع إحصائية اختبار T توزيعًا بدرجات حرية n-2.

دعونا نراجع مثالاً لكيفية اختبار أهمية معامل ارتباط بيرسون.

مثال

توضح مجموعة البيانات التالية طول ووزن 12 فردًا:

يوضح مخطط التشتت أدناه قيمة هذين المتغيرين:

معامل ارتباط بيرسون لهذين المتغيرين هو r = 0.836.

إحصائية الاختبار T = 0.836 * √ (12 -2) / (1-0.836 ² ) = 4.804.

وفقًا لآلة حاسبة توزيع t الخاصة بنا، فإن النتيجة 4.804 مع 10 درجات حرية لها قيمة p تبلغ 0.0007. بما أن 0.0007 <0.05، يمكننا أن نستنتج أن الارتباط بين الوزن والطول في هذا المثال له دلالة إحصائية عند ألفا = 0.05.

احتياطات

على الرغم من أن معامل ارتباط بيرسون يمكن أن يكون مفيدًا في إخبارنا ما إذا كان هناك ارتباط خطي بين متغيرين أم لا، إلا أننا نحتاج إلى وضع ثلاثة أشياء في الاعتبار عند تفسير معامل ارتباط بيرسون:

1. الارتباط لا يعني السببية. ليس بسبب وجود متغيرين مترابطين، فإن أحدهما يؤدي بالضرورة إلى ظهور الآخر في كثير من الأحيان أو أقل. والمثال الكلاسيكي على ذلك هو العلاقة الإيجابية بين مبيعات الآيس كريم وهجمات أسماك القرش. عندما تزيد مبيعات الآيس كريم في أوقات معينة من السنة، تميل هجمات أسماك القرش أيضًا إلى الزيادة.

هل هذا يعني أن تناول الآيس كريم يسبب هجمات أسماك القرش؟ بالطبع لا! وهذا يعني ببساطة أنه في فصل الصيف، يميل استهلاك الجليد وهجمات أسماك القرش إلى الزيادة، لأن الجليد أكثر شيوعًا في الصيف ويذهب المزيد من الناس إلى المحيط خلال فصل الصيف.

2. الارتباطات حساسة للقيم المتطرفة. يمكن للقيمة المتطرفة أن تغير بشكل كبير معامل ارتباط بيرسون. خذ بعين الاعتبار المثال أدناه:

المتغيران X و Y لهما معامل ارتباط بيرسون 0.00 . لكن تخيل أن لدينا قيمة متطرفة في مجموعة البيانات:

ومع ذلك فإن معامل ارتباط بيرسون لهذين المتغيرين هو 0.878 . هذا الغريب يغير كل شيء. ولهذا السبب، عند حساب الارتباط بين متغيرين، من الجيد تصور المتغيرات باستخدام مخطط التشتت للتحقق من القيم المتطرفة.

3. لا يلتقط معامل ارتباط بيرسون العلاقات غير الخطية بين متغيرين. لنتخيل أن لدينا متغيرين بالعلاقة التالية:

معامل ارتباط بيرسون لهذين المتغيرين هو 0.00 لعدم وجود علاقة خطية بينهما. ومع ذلك، فإن هذين المتغيرين لهما علاقة غير خطية: قيم y هي ببساطة قيم x مربعة.

عند استخدام معامل ارتباط بيرسون، ضع في اعتبارك أنك تقوم ببساطة باختبار ما إذا كان هناك متغيرين مرتبطين خطيًا . حتى لو أخبرنا معامل ارتباط بيرسون أن متغيرين غير مرتبطين، فمن الممكن أن يكون لهما نوع من العلاقة غير الخطية. وهذا سبب آخر يجعل من المفيد إنشاء مخطط مبعثر عند تحليل العلاقة بين متغيرين: يمكن أن يساعدك في اكتشاف علاقة غير خطية.