معامل ارتباط بيرسون
تشرح هذه المقالة ما هو معامل ارتباط بيرسون (أو معامل الارتباط الخطي) وما هو استخدامه. سوف تكتشف كيفية حساب معامل ارتباط بيرسون مع تمرين خطوة بخطوة. بالإضافة إلى ذلك، يمكنك العثور على قيمة معامل ارتباط بيرسون لأي مجموعة بيانات باستخدام الآلة الحاسبة عبر الإنترنت في النهاية.
ما هو معامل ارتباط بيرسون؟
معامل ارتباط بيرسون ، ويسمى أيضًا معامل الارتباط الخطي أو ببساطة معامل الارتباط ، هو مقياس إحصائي يشير إلى العلاقة بين متغيرين.
لحساب معامل ارتباط بيرسون بين متغيرين، يجب عليك قسمة تباين المتغيرات المذكورة على الجذر التربيعي لحاصل ضرب تبايناتها.
وبالتالي، يحاول معامل ارتباط بيرسون قياس الاعتماد الخطي بين متغيرين عشوائيين كميين. بداهة، يعد تقييم الارتباط بين المتغيرات رقميًا أمرًا معقدًا لأنه من الصعب تحديد ما إذا كان زوج المتغيرات أكثر ارتباطًا بين ما إذا كان هدف معامل ارتباط بيرسون، كما هو الحال في pus، هو تقييم العلاقة بين المتغيرات لتكون قادرًا على ذلك قارن بينهما.
تتراوح قيمة مؤشر ارتباط بيرسون بين -1 و+1 ضمناً. سنرى أدناه كيفية تفسير قيمة معامل ارتباط بيرسون.
صيغة معامل ارتباط بيرسون
إن معامل ارتباط بيرسون لمتغيرين إحصائيين يساوي حاصل الضرب بين تباين المتغيرات والجذر التربيعي لحاصل ضرب تباين كل متغير.
ولذلك، فإن صيغة حساب معامل ارتباط بيرسون هي كما يلي:
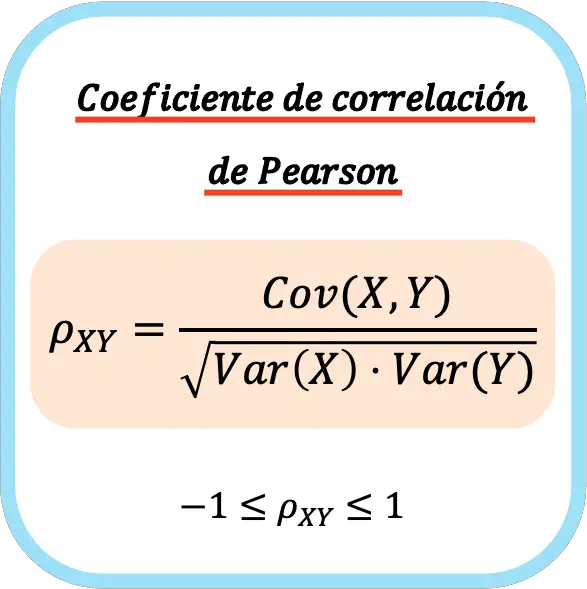
👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب معامل ارتباط بيرسون لأي مجموعة بيانات.
عندما يتم حساب معامل ارتباط بيرسون على عدد السكان، يتم التعبير عنه عمومًا بالحرف اليوناني ρ. ولكن عندما يتم حساب المعامل بالنسبة لعينة، عادة ما يستخدم الحرف r كرمز.
ضع في اعتبارك أنه لتحديد معامل ارتباط بيرسون، من الضروري أن تعرف كيفية حساب التباين بين متغيرين وتباين المتغير. بالإضافة إلى ذلك، عليك أن تفهم ما تعنيه هذه القياسات الإحصائية. لذلك، قبل الاستمرار في الشرح، ينصح بقراءة المقالين التاليين:
مثال لحساب معامل ارتباط بيرسون
بالنظر إلى تعريف معامل ارتباط بيرسون وصيغته، يوجد أدناه مثال خطوة بخطوة حتى تتمكن من معرفة كيفية حسابه.
- احسب معامل ارتباط بيرسون بين المتغيرين المستمرين التاليين:

قبل حساب معامل ارتباط بيرسون، سنقوم بتمثيل مجموعة البيانات في مخطط التشتت لتحليل العلاقة بين المتغيرين:
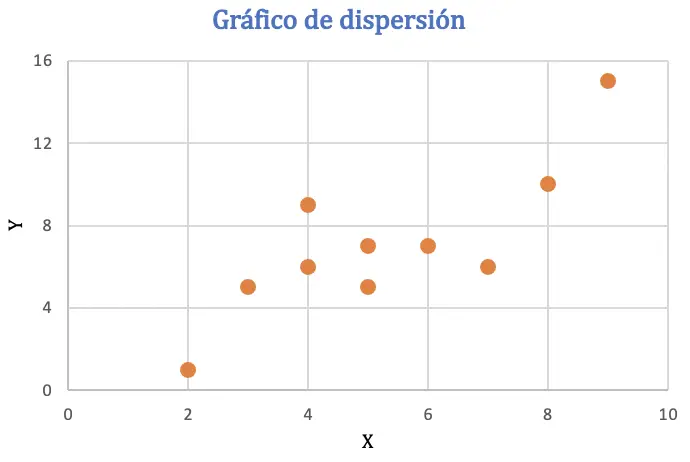
من المخطط المبعثر، يمكن استنتاج أن البيانات قد يكون لها اتجاه إيجابي، أو بمعنى آخر، عندما تزيد قيمة متغير واحد، يزداد المتغير الآخر أيضًا. وللتحقق من الارتباط، سنجد معامل بيرسون.
أول ما يجب فعله هو إيجاد الوسط الحسابي لكل متغير على حدة، وهو ما يعادل مجموع البيانات مقسومًا على عدد الملاحظات.
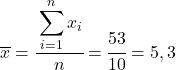
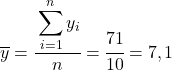
الآن بعد أن عرفنا متوسط كل متغير، نحتاج إلى إضافة الأعمدة التالية إلى جدول البيانات:
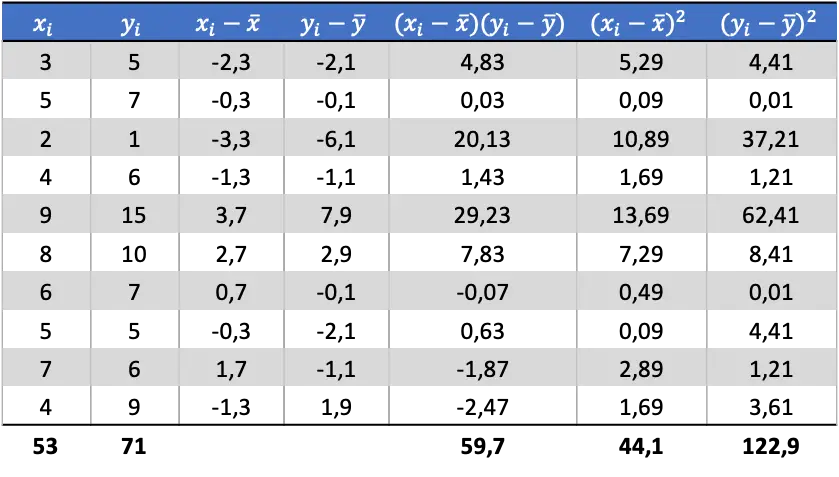
من البيانات المحسوبة في الجدول، نحدد قيم التباين والتباينات (إذا كنت لا تتذكر كيف تم ذلك، هناك رابطان أعلاه حيث يتم شرح ذلك بالتفصيل):
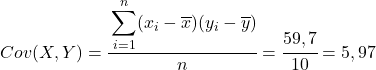
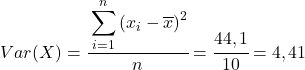
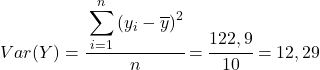
أخيرًا، ما عليك سوى تطبيق صيغة معامل ارتباط بيرسون للحصول على قيمتها:
![]()
معامل ارتباط بيرسون له قيمة قريبة جدًا من 1، مما يعني أن هذين المتغيرين لهما علاقة إيجابية قوية إلى حد ما.
كما رأيت، لتحديد معامل ارتباط بيرسون، من المفيد جدًا استخدام برامج مثل Excel لإجراء حسابات الأعمدة بسرعة أكبر.
حاسبة معامل الارتباط بيرسون
أدخل مجموعة من البيانات الإحصائية في الآلة الحاسبة التالية لحساب معامل ارتباط بيرسون بين متغيرين. تحتاج إلى فصل أزواج البيانات، بحيث يوجد في المربع الأول قيم متغير واحد فقط وفي المربع الثاني توجد قيم المتغير الثاني فقط.
يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.
تفسير معامل ارتباط بيرسون
سنرى في هذا القسم كيفية تفسير معامل ارتباط بيرسون، لأنه لا يكفي أن تعرف قيمته، بل يجب أن تعرف كيف تحلل معناه.
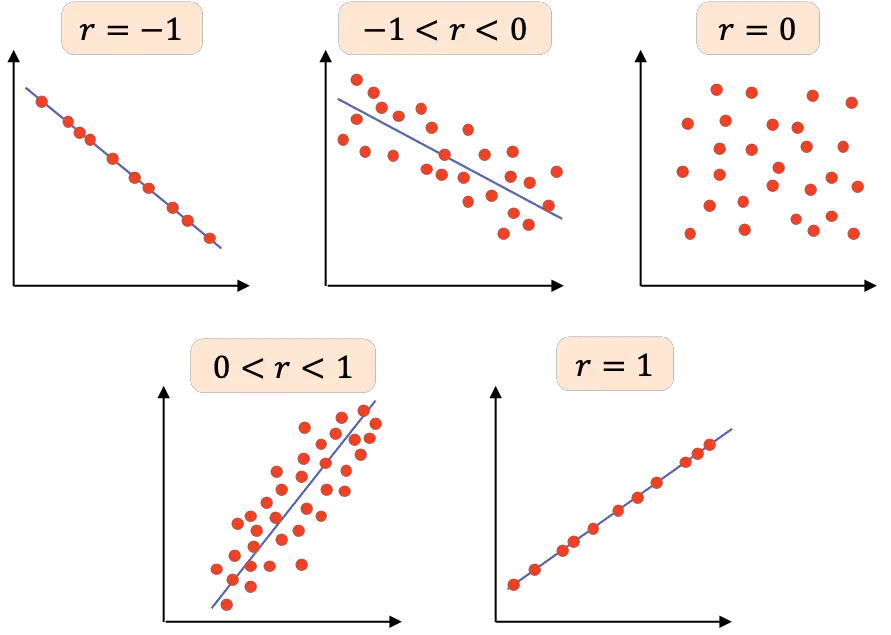
وبالتالي فإن تفسير معامل ارتباط بيرسون يعتمد على قيمته:
- r=-1 : المتغيران لهما علاقة سلبية تامة، حتى نتمكن من رسم خط ذو ميل سلبي ترتبط فيه جميع النقاط.
- -1<r<0 : الارتباط بين المتغيرين سلبي، فإذا زاد أحد المتغيرين انخفض الآخر. كلما كانت القيمة أقرب إلى -1، كلما كانت العلاقة بين المتغيرات أكثر سلبية.
- r=0 : الارتباط بين المتغيرين ضعيف جداً، في الواقع العلاقة الخطية بينهما صفر. وهذا لا يعني أن المتغيرات مستقلة، حيث يمكن أن تكون لها علاقة غير خطية.
- 0<r<1 : تكون العلاقة بين المتغيرين موجبة، وكلما اقتربت القيمة من +1، كانت العلاقة بين المتغيرين أقوى. في هذه الحالة، يميل أحد المتغيرات إلى الزيادة في القيمة عندما يزيد الآخر أيضًا.
- r=1 : المتغيران لهما علاقة إيجابية تامة، أي أن لديهما علاقة خطية موجبة.
وباختصار، يعرض الجدول التالي التفسيرات المختلفة لمعامل ارتباط بيرسون:
| قيمة | تفسير |
|---|---|
| ص=-1 | الارتباط السلبي الكامل. |
| -1<ص<0 | الارتباط السلبي: كلما اقترب الارتباط من -1، كان أقوى. |
| ص = 0 | الارتباط الخطي صفر. |
| 0<ص<1 | الارتباط الإيجابي: كلما كان الارتباط أقرب إلى +1، كان أقوى. |
| ص = 1 | علاقة إيجابية مثالية. |
وتذكر أنه حتى لو كانت هناك علاقة بين متغيرين، فهذا لا يعني أن هناك علاقة سببية بينهما، أي أن الارتباط بين متغيرين لا يعني أن تغير المتغير هو سبب تغير المتغير. متغير آخر.
فمثلاً، إذا وجدنا أن هناك علاقة إيجابية بين إنتاج هرمونين مختلفين في الجسم، فليس من الضروري أن تؤدي زيادة أحد الهرمونين إلى زيادة الهرمون الآخر. ومن الممكن أن ينتج الجسم كلا الهرمونين لأنه يحتاج إلى كليهما لمحاربة المرض، وبالتالي يزيد من مستوياتهما في وقت واحد، وفي هذه الحالة يكون السبب هو المرض. لتحديد ما إذا كانت هناك علاقة سببية بين الهرمونين، ينبغي إجراء مزيد من الدراسة.