كيفية مقارنة الرسوم البيانية (مع أمثلة)

الرسم البياني هو نوع من المخططات التي تسمح لنا بتصور توزيع القيم في مجموعة من البيانات.

يُظهر المحور X قيم مجموعة البيانات ويُظهر المحور Y تكرار كل قيمة.

تعد الرسوم البيانية مفيدة لأنها تتيح لنا فهم توزيع القيم في مجموعة البيانات بسرعة. كما أنها مفيدة لمقارنة مجموعتين مختلفتين من البيانات.

عند مقارنة اثنين أو أكثر من الرسوم البيانية، يمكننا الإجابة على ثلاثة أسئلة مختلفة:

1. كيف تتم مقارنة القيم المتوسطة؟

يمكننا أن نقدر تقريبًا أن الوسيط يقع بالقرب من منتصف كل رسم بياني، مما يسمح لنا بمقارنة القيم المتوسطة للتوزيعات.

2. كيف يمكن مقارنة التشتت؟

يمكننا أن نرى بصريًا الرسم البياني الأكثر انتشارًا، مما يعطينا فكرة عن التوزيع الذي يحتوي على قيم أكثر تشتتًا.

3. كيف يمكن مقارنة عدم التماثل؟

إذا كان الرسم البياني يحتوي على “ذيل” على الجانب الأيسر من المخطط، فيقال أنه منحرف بشكل سلبي. على العكس من ذلك، إذا كان الرسم البياني يحتوي على “ذيل” على الجانب الأيمن من المخطط، فيقال أنه منحرف بشكل إيجابي. يمكننا التحقق بصريًا من كل رسم بياني لمقارنة الانحراف .

يوضح المثال التالي كيفية مقارنة رسمين بيانيين مختلفين والإجابة على هذه الأسئلة الثلاثة.

مثال: مقارنة الرسوم البيانية

لنفترض أن 200 طالب يستخدمون طريقة دراسة واحدة للتحضير للاختبار وأن 200 طالب آخرين يستخدمون طريقة دراسة مختلفة للتحضير لنفس الاختبار.

لنفترض أننا أنشأنا الرسوم البيانية التالية لمقارنة نتائج الامتحانات لكل مجموعة من الطلاب:

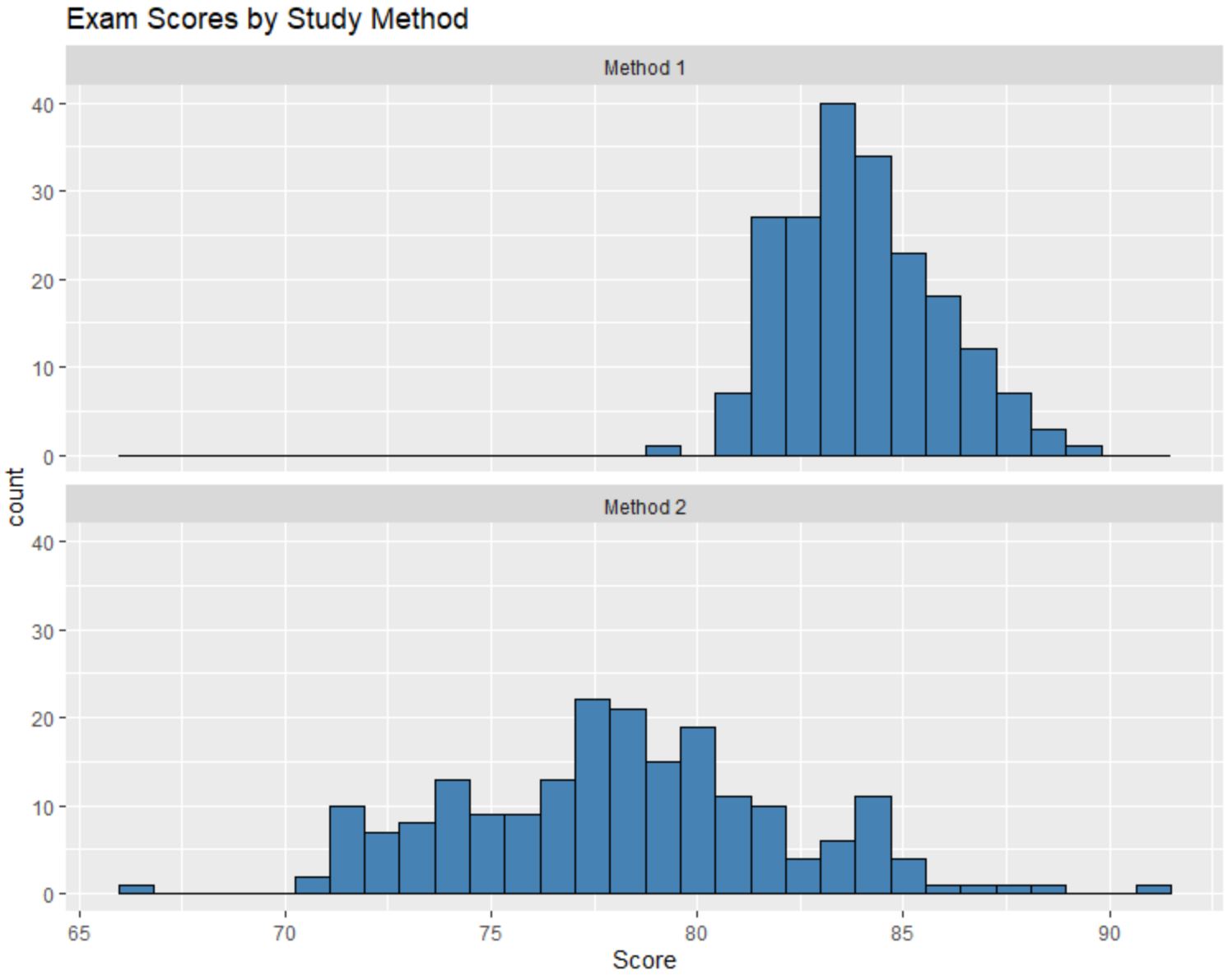
يمكننا مقارنة هذه الرسوم البيانية والإجابة على الأسئلة الثلاثة التالية:

1. كيف تتم مقارنة القيم المتوسطة؟

على الرغم من أننا لا نعرف القيم المتوسطة الدقيقة لكل توزيع بمجرد النظر إلى الرسوم البيانية، فمن الواضح أن متوسط درجات الاختبار للطلاب الذين استخدموا الطريقة الأولى أعلى من متوسط درجات الاختبار للطلاب الذين استخدموا الطريقة الأولى. الطريقة 2 .

يمكننا تقدير أن القيمة المتوسطة للطريقة 1 تبلغ حوالي 84 والقيمة المتوسطة للطريقة 2 تبلغ حوالي 78.

2. كيف يمكن مقارنة التشتت؟

تعد قيم الرسم البياني للطريقة الثانية أكثر تشتتًا بكثير من قيم الطريقة الأولى، مما يخبرنا أن هناك تشتتًا أكبر بكثير في نتائج الاختبار للطلاب الذين استخدموا الطريقة الثانية.

3. كيف يمكن مقارنة عدم التماثل؟

بالنظر إلى الرسوم البيانية، يبدو أن توزيع درجات الاختبار للطريقة الأولى منحرف قليلاً إلى اليمين، كما يتضح من “الذيل” الممتد إلى يمين الرسم البياني.

ومع ذلك، لا يبدو أن هناك “ذيل” في توزيع نتائج الاختبار للطريقة الثانية، مما يخبرنا أن التوزيع قليل أو غير منحرف.

المكافأة : إليك الكود الذي استخدمناه في R لإنشاء هذين الرسمين البيانيين:

 library (ggplot2)

#make this example reproducible
set. seeds (0)

#create data frame
df <- data. frame (method=rep(c(' Method 1 ', ' Method 2 '), each= 200 ),
                 Score=c(rnorm( 200 , mean= 84 , sd= 2 ),
                         rnorm( 200 , mean= 78 , sd= 4 )))

#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
  geom_histogram(fill=' steelblue ', color=' black ') +
  facet_wrap(.~method, nrow= 2 ) +
  labs(title=' Exam Scores by Study Method ')

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية تنفيذ المهام الشائعة الأخرى باستخدام الرسوم البيانية:

كيفية تقدير المتوسط والوسيط لأي رسم بياني
كيفية تقدير الانحراف المعياري لأي رسم بياني
كيفية وصف شكل الرسوم البيانية