كيفية إنشاء وتفسير منحنى roc في spss

الانحدار اللوجستي هو طريقة إحصائية نستخدمها لتناسب نموذج الانحدار عندما يكون متغير الاستجابة ثنائيًا. لتقييم مدى ملاءمة نموذج الانحدار اللوجستي لمجموعة البيانات، يمكننا النظر إلى المقياسين التاليين:

• الحساسية: احتمال أن يتنبأ النموذج بنتيجة إيجابية لملاحظة ما عندما تكون النتيجة إيجابية بالفعل.
• الخصوصية: احتمال أن يتنبأ النموذج بنتيجة سلبية لملاحظة ما عندما تكون النتيجة سلبية بالفعل.

إحدى الطرق البسيطة لتصور هذين المقياسين هي إنشاء منحنى ROC ، وهو رسم بياني يعرض حساسية وخصوصية نموذج الانحدار اللوجستي.

يشرح هذا البرنامج التعليمي كيفية إنشاء وتفسير منحنى ROC في برنامج SPSS.

مثال: منحنى ROC في برنامج SPSS

لنفترض أن لدينا مجموعة البيانات التالية التي توضح ما إذا كان لاعب كرة السلة قد تم تجنيده في الدوري الاميركي للمحترفين أم لا (0 = لا، 1 = نعم) بالإضافة إلى متوسط نقاطه لكل مباراة في الكلية:

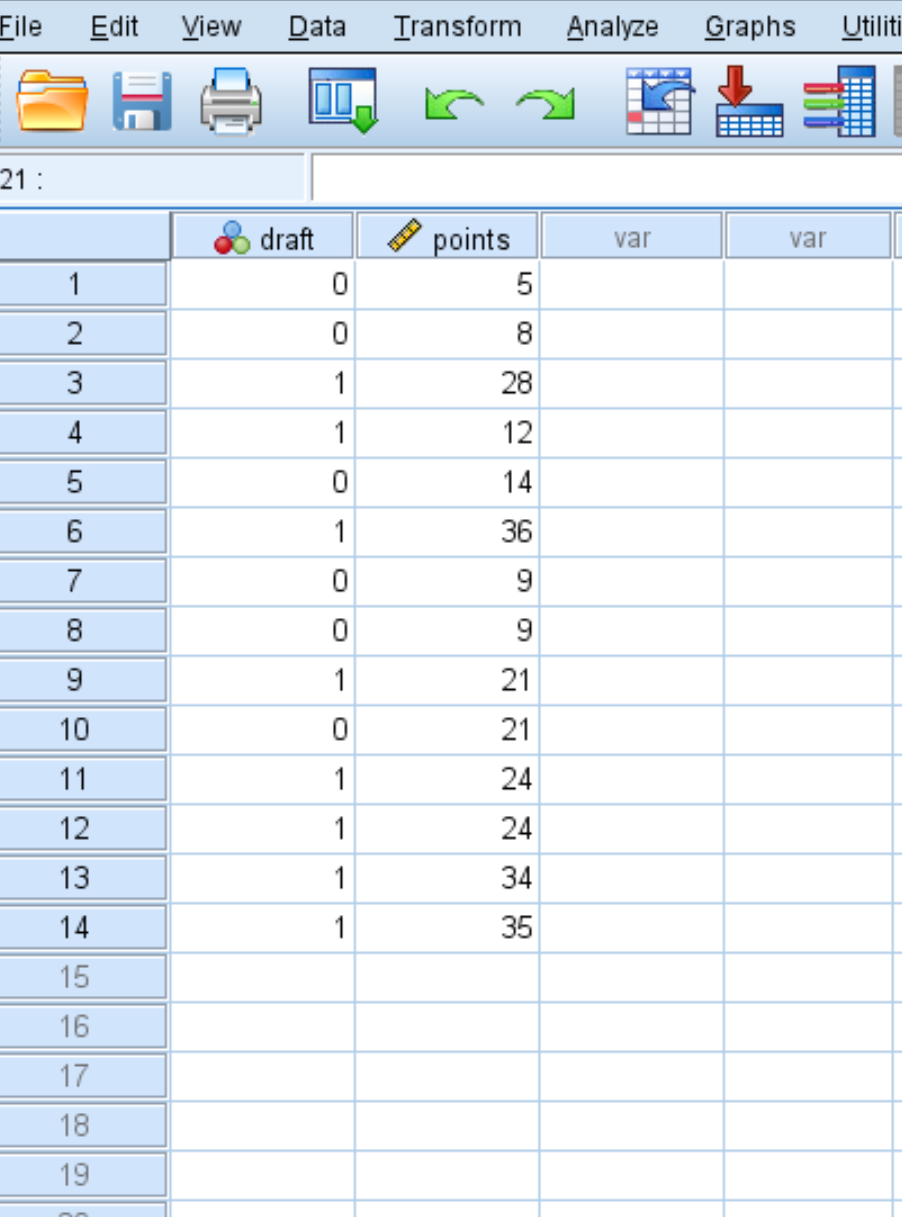
لإنشاء منحنى ROC لمجموعة البيانات هذه، انقر فوق علامة التبويب تحليل ، ثم تصنيف ، ثم منحنى ROC :

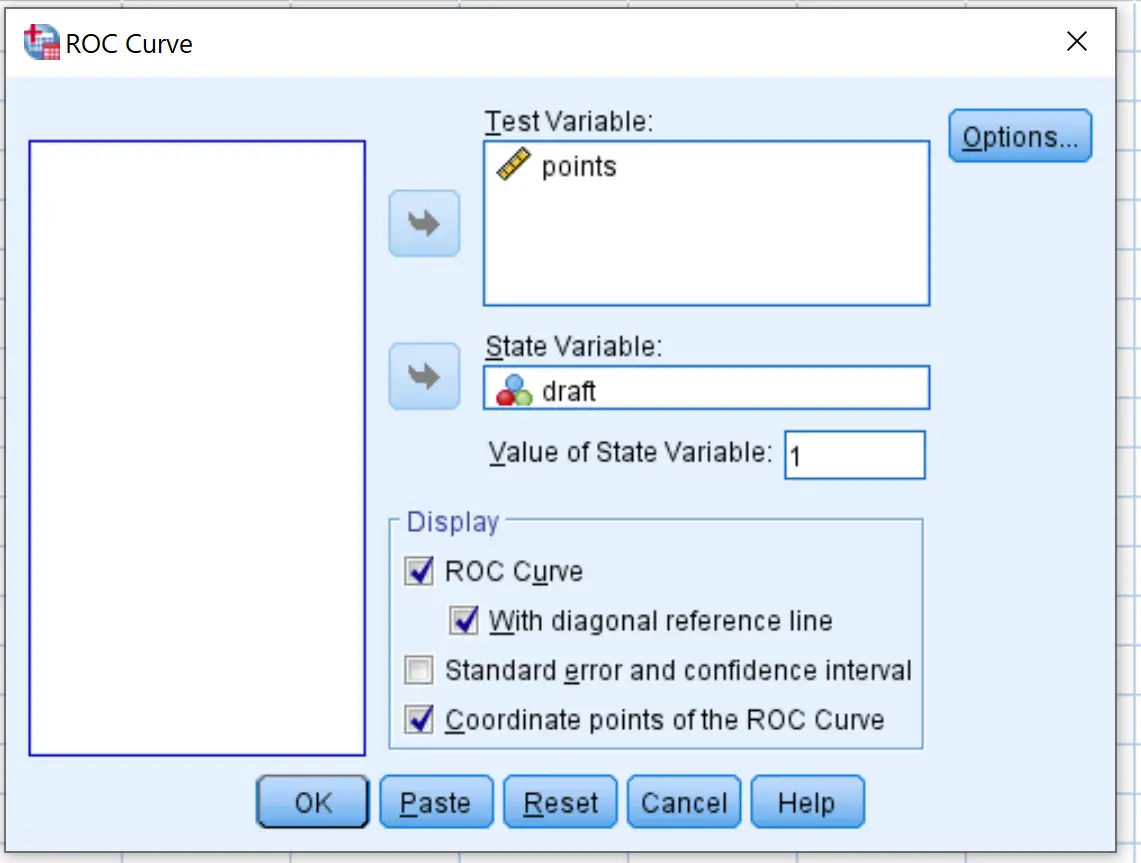
في النافذة الجديدة التي تظهر، اسحب متغير المسودة إلى المنطقة المسماة متغير الحالة. اضبط قيمة متغير الحالة على 1 . (هذه هي القيمة التي تشير إلى أن اللاعب قد تمت صياغته). اسحب نقاط المتغير إلى المنطقة المسماة اختبار المتغير.

حدد المربعات المجاورة لـ مع الخط المرجعي القطري وإحداثيات نقطة منحنى ROC . ثم انقر فوق موافق .

وإليك كيفية تفسير النتيجة:

ملخص معالجة الملف:

يعرض هذا الجدول إجمالي عدد الحالات الإيجابية والسلبية في مجموعة البيانات. في هذا المثال، تمت صياغة 8 لاعبين (نتيجة إيجابية) ولم تتم صياغة 6 لاعبين (نتيجة سلبية):

منحنى روك:

منحنى خاصية تشغيل المستقبِل (ROC) عبارة عن مخطط لقيم الحساسية مقابل الخصوصية 1 حيث تتغير قيمة العتبة من 0 إلى 1:

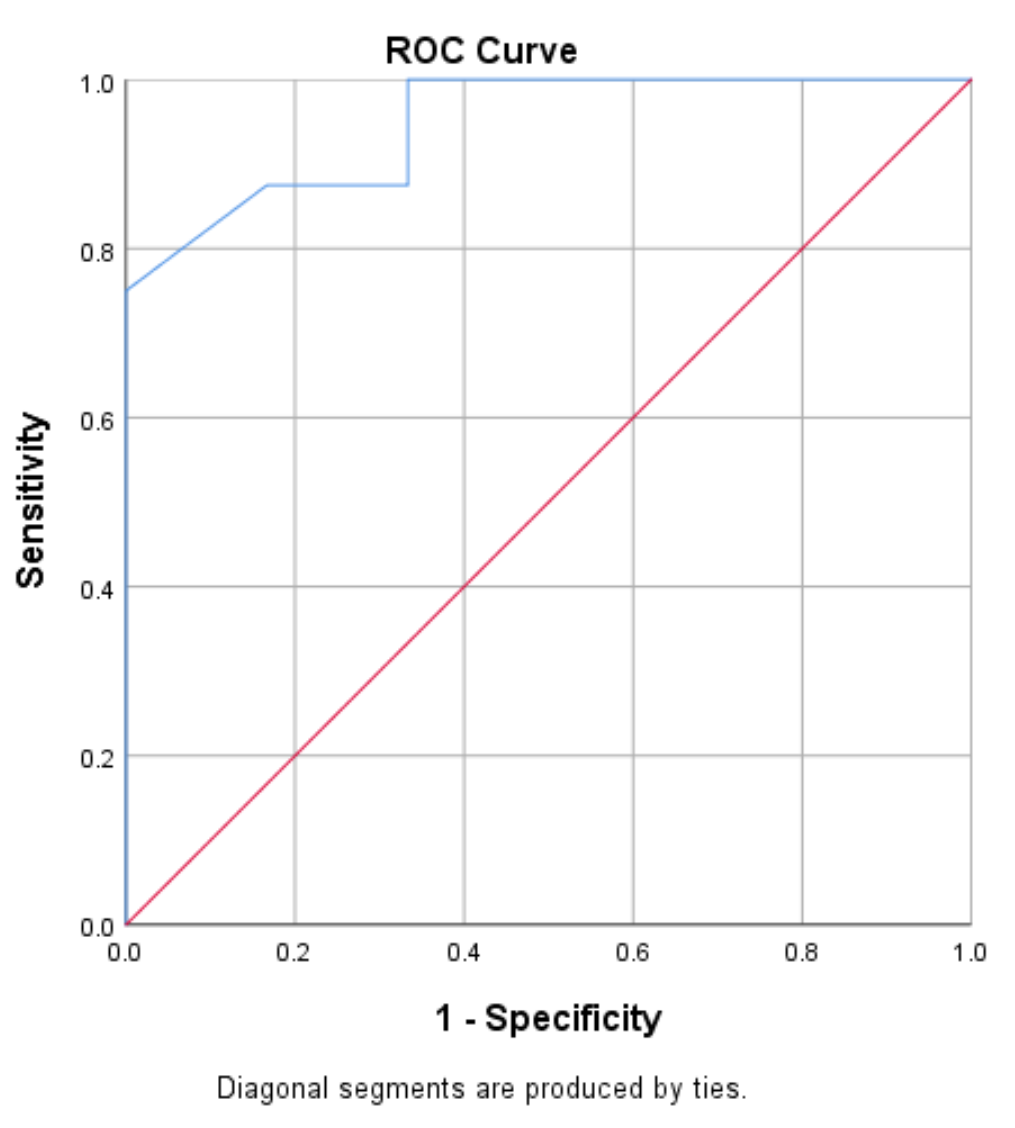
سيكون للنموذج ذو الحساسية والخصوصية العالية منحنى ROC يناسب الزاوية اليسرى العليا من المخطط. سيكون للنموذج ذو الحساسية المنخفضة والخصوصية المنخفضة منحنى قريب من قطري 45 درجة.

يمكننا أن نرى أن منحنى ROC (الخط الأزرق) في هذا المثال يعانق الزاوية اليسرى العليا من الحبكة، مما يشير إلى أن النموذج يقوم بعمل جيد في التنبؤ باللاعبين سواء سيتم تجنيدهم أم لا، بناءً على متوسط نقاطهم في كل مباراة. . .

المساحة تحت المنحنى:

تعطينا المساحة الموجودة أسفل المنحنى فكرة عن قدرة النموذج على التمييز بين النتائج الإيجابية والسلبية. يمكن أن تتراوح المساحة تحت المنحنى من 0 إلى 1. وكلما ارتفعت المساحة تحت المنحنى، كان النموذج أفضل في تصنيف النتائج بشكل صحيح.

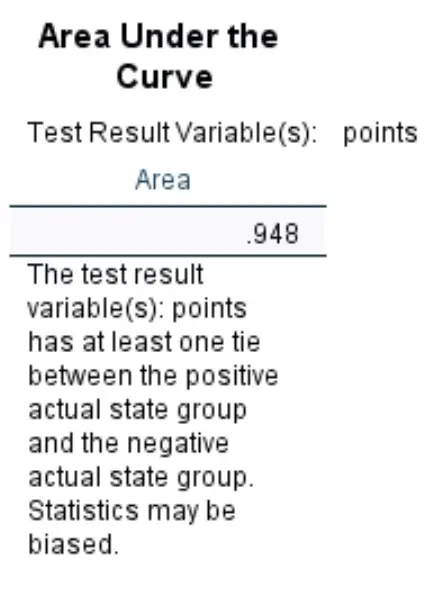
يمكننا أن نرى أن AUC لنموذج الانحدار اللوجستي هذا هو 0.948 ، وهو مرتفع للغاية. يشير هذا إلى أن النموذج يقوم بعمل جيد في التنبؤ بما إذا كان سيتم تجنيد اللاعب أم لا.

إحداثيات المنحنى:

يعرض هذا الجدول الأخير حساسية وخصوصية 1 لمنحنى ROC لعتبات مختلفة.

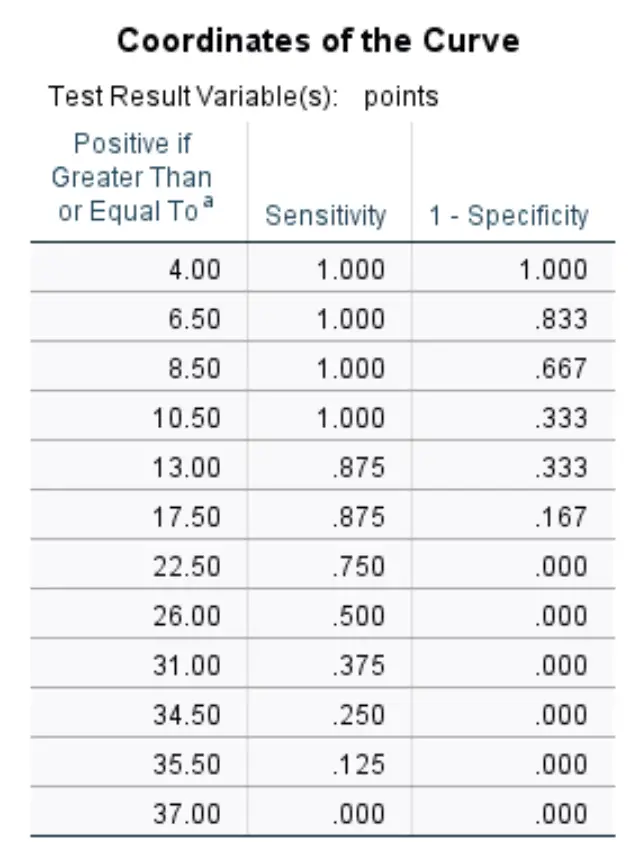
على سبيل المثال:

إذا سمحنا أن تكون العتبة 8.50 ، فهذا يعني أننا نتوقع أن أي لاعب يسجل أقل من 8.50 نقطة في المباراة الواحدة لن تتم صياغته، وأن أي لاعب يسجل أكثر من 8.50 نقطة في المباراة الواحدة ستتم صياغته.

باستخدام هذا كعتبة، ستكون حساسيتنا 100% (نظرًا لأن كل لاعب سجل أقل من 8.50 نقطة في كل مباراة لم يتم تجنيده بالفعل) وستكون خصوصيتنا 1 66.7% (نظرًا لأن 8 لاعبين من أصل 12 سجلوا أكثر من 8.50 نقطة) تمت صياغة كل لعبة).

يتيح لنا الجدول أعلاه رؤية الحساسية والنوعية 1 لكل عتبة محتملة.