ما هي منحنيات الكثافة؟ (شرح وأمثلة)

منحنى الكثافة هو منحنى على الرسم البياني الذي يمثل توزيع القيم في مجموعة من البيانات. وهذا مفيد لثلاثة أسباب:

1. يمنحنا منحنى الكثافة فكرة جيدة عن “شكل” التوزيع، بما في ذلك ما إذا كان التوزيع يحتوي على “ذروة” واحدة أو أكثر من قيم التردد أم لا وما إذا كان التوزيع منحرفًا إلى اليسار أم لا صحيح. يمين. .

2. يتيح لنا منحنى الكثافة أن نرى بصريًا أين يرتبط متوسط ووسيط التوزيع.

3. يتيح لنا منحنى الكثافة أن نرى بصريًا النسبة المئوية للملاحظات في مجموعة البيانات التي تقع بين قيم مختلفة.

منحنى الكثافة الأكثر شهرة هو منحنى الجرس الذي يمثل التوزيع الطبيعي .

لفهم منحنيات الكثافة بشكل أفضل، خذ بعين الاعتبار المثال التالي.

مثال: إنشاء وتفسير منحنى الكثافة

لنفترض أن لدينا مجموعة البيانات التالية التي توضح ارتفاع 20 نباتًا مختلفًا (بالبوصة) في حقل معين:

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

إذا قمنا بإنشاء رسم بياني بسيط لعرض التكرارات النسبية لكل قيمة، فسيبدو كما يلي:

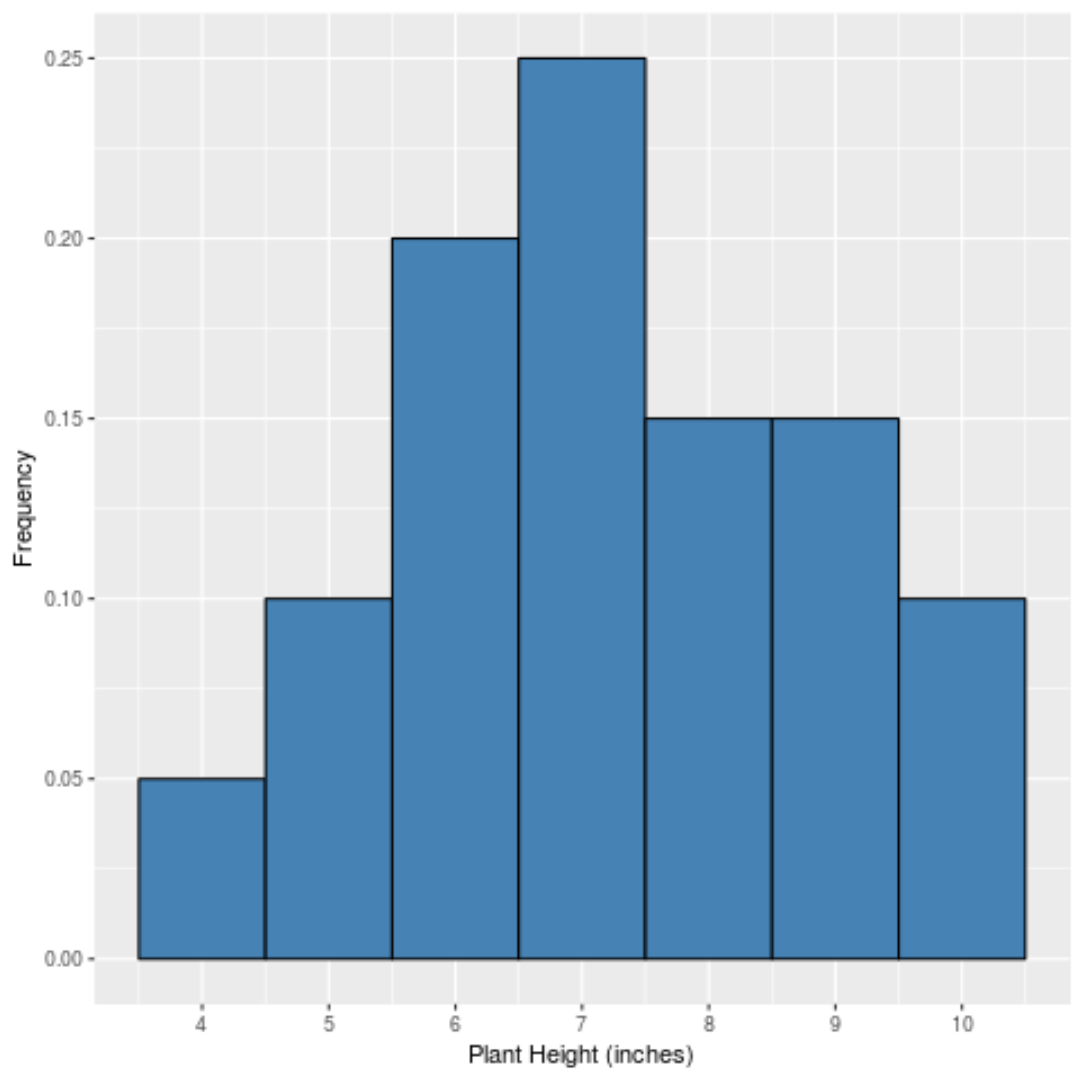
يعرض المحور “س” قيمة البيانات والمحور “ص” يظهر التكرار النسبي (على سبيل المثال، تظهر القيمة “7” 5 مرات من أصل 20 قيمة إجمالية في مجموعة البيانات، لذلك يكون التكرار النسبي 25٪ أو 0.25 .

وإذا أنشأنا منحنى الكثافة لالتقاط “شكل” هذا التوزيع، فسيبدو كما يلي:

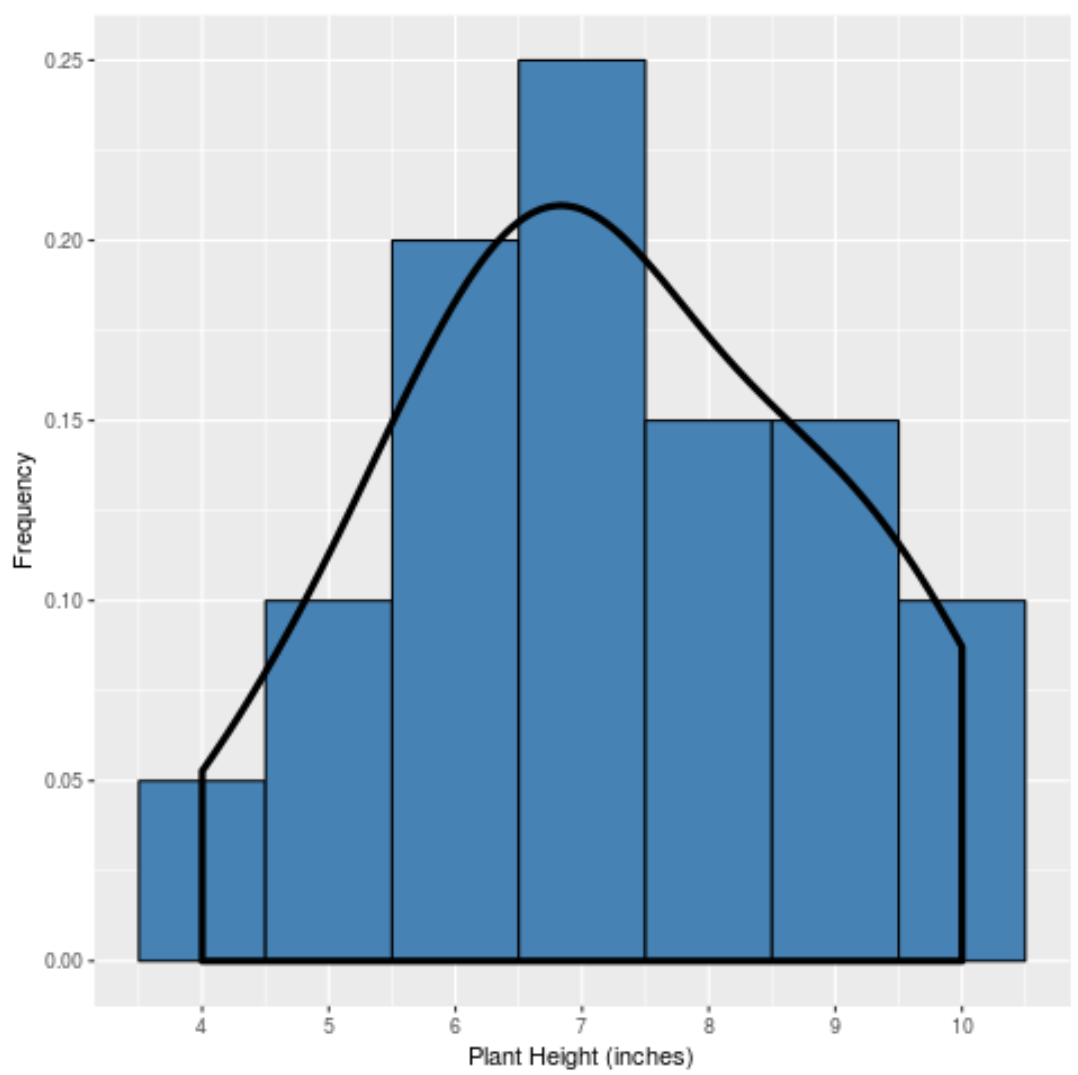
يكون المنحنى في أعلى مستوياته بالقرب من مركز التوزيع لأنه يوجد فيه معظم القيم. كما أنها تكون في أدنى مستوياتها بالقرب من أطراف التوزيع لأن عددًا أقل من النباتات يأخذ هذه القيم (على سبيل المثال الارتفاع 4 بوصات أو 10 بوصات).

كيفية تفسير منحنيات الكثافة

تأتي منحنيات الكثافة بجميع الأشكال والأحجام وتتيح لنا الحصول على فهم مرئي سريع لتوزيع القيم في مجموعة بيانات معينة. إنها مفيدة بشكل خاص لمساعدتنا في تصور:

1. عدم التماثل

الانحراف هو وسيلة لوصف التماثل في التوزيع. تسمح لنا منحنيات الكثافة بمعرفة ما إذا كان الرسم البياني مائلًا إلى اليسار أو اليمين أو لا يوجد به أي ميل بسرعة:

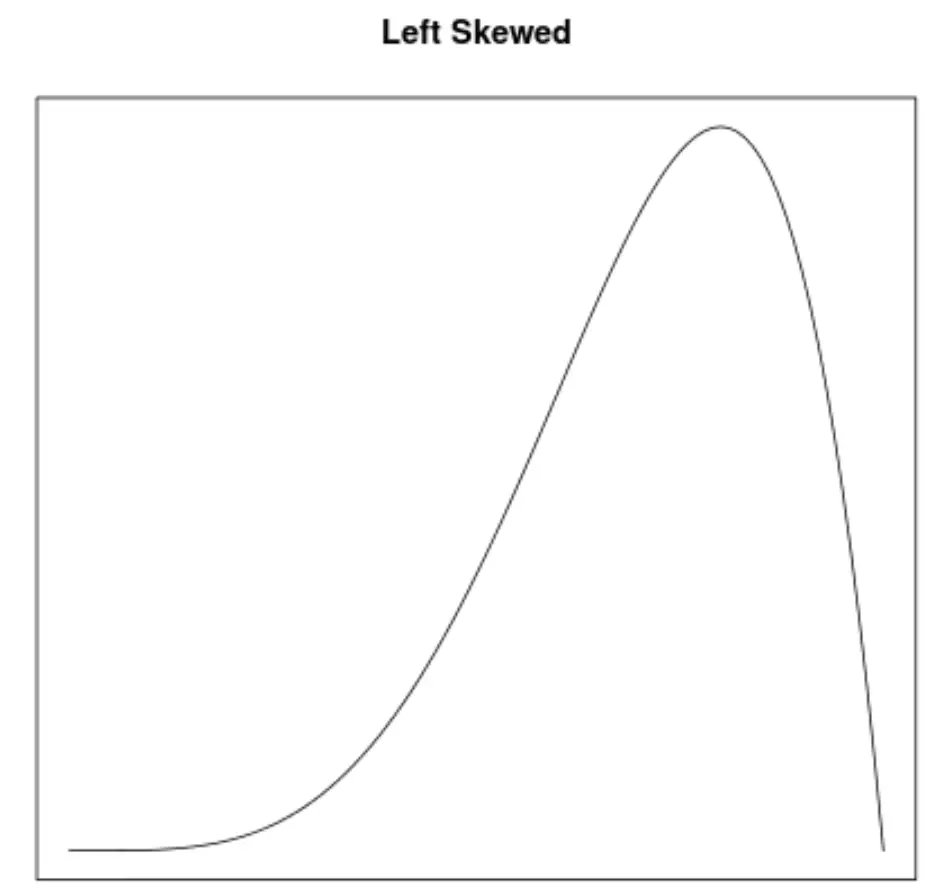
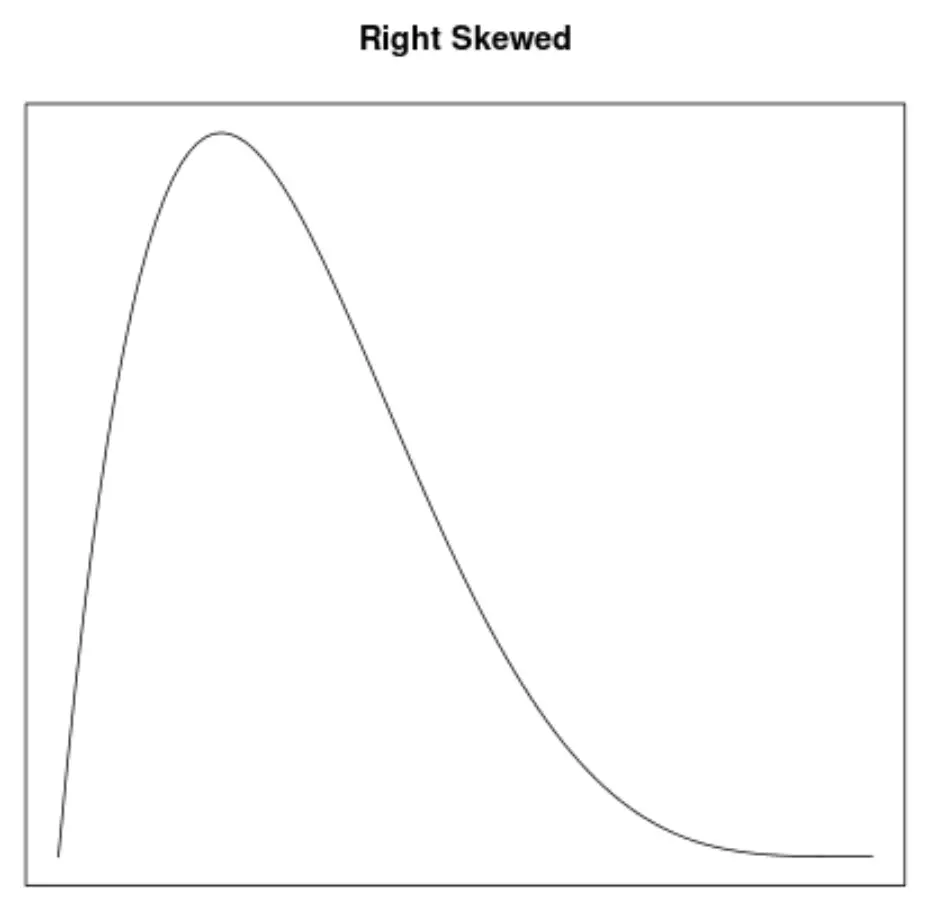
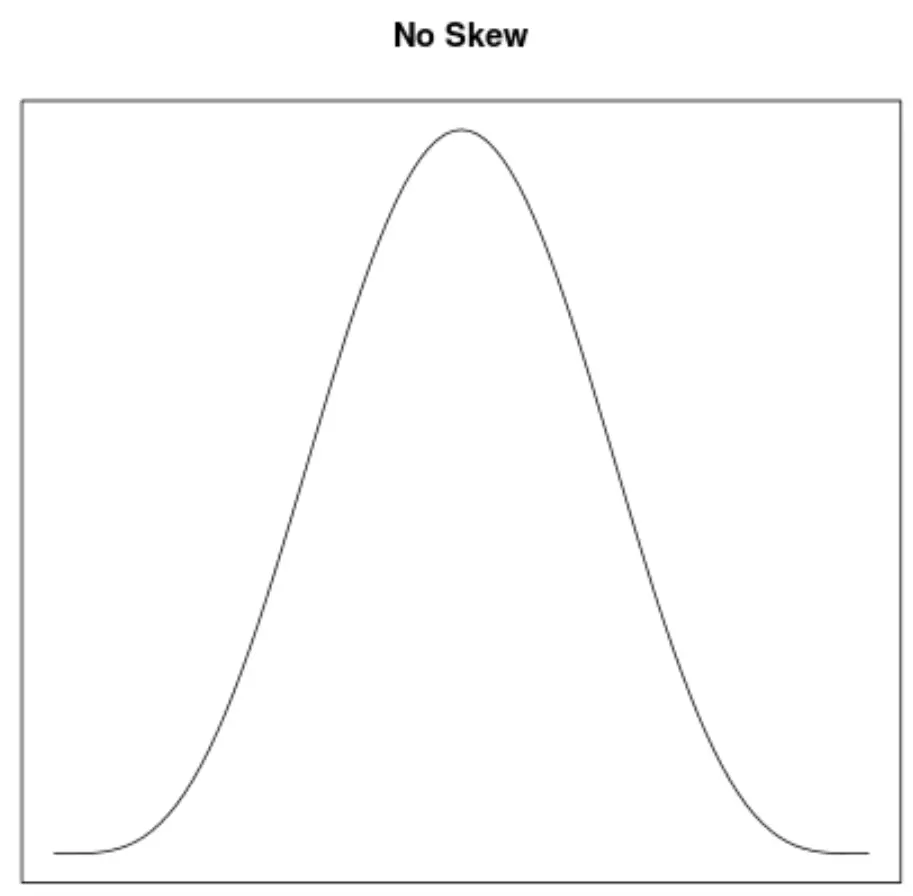
2. موقع الوسط والوسيط

استنادًا إلى انحراف منحنى الكثافة، يمكننا أن نعرف بسرعة ما إذا كان المتوسط أو الوسيط أكبر في توزيع معين. خصوصاً:

• إذا ظل منحنى الكثافة غير متماثل ، فإن المتوسط يكون أقل من المتوسط.
• إذا كان منحنى الكثافة منحرفًا إلى اليمين ، فإن المتوسط أكبر من الوسيط.
• إذا لم يكن لمنحنى الكثافة عدم تماثل ، فإن المتوسط يساوي الوسيط.

3. عدد القمم

تسمح لنا منحنيات الكثافة أيضًا برؤية عدد “القمم” الموجودة في توزيع معين بسرعة. في كل من الأمثلة المذكورة أعلاه، كان للتوزيعات ذروة واحدة فقط، لذلك يمكننا وصف هذه التوزيعات بأنها أحادية الواسطة .

ومع ذلك، يمكن أن تحتوي بعض التوزيعات على ذروتين نسميهما التوزيعات الثنائية . وفي حالات نادرة يمكن أن يكون لدينا أيضًا توزيعات متعددة الوسائط ذات قمتين أو أكثر.

بمجرد إنشاء منحنى الكثافة لمجموعة بيانات معينة، يمكننا أن نرى بسرعة عدد القمم الموجودة في التوزيع.

خصائص منحنيات الكثافة

تتميز منحنيات الكثافة بالخصائص التالية:

• دائمًا ما يصل مجموع المساحة الموجودة أسفل المنحنى إلى 100%.
• لن ينخفض المنحنى أبدًا عن المحور السيني.

ضع هاتين الحقيقتين في الاعتبار عند إنشاء أو تفسير منحنيات الكثافة لتوزيعات مختلفة.

مصادر إضافية

مقدمة في الرسوم البيانية للتردد النسبي
كيفية إنشاء منحنى الجرس في إكسل
كيفية إنشاء منحنى الجرس في بايثون