ما هي ذاتية موران؟ (التعريف & #038؛ مثال)

Moran’s I هي طريقة لقياس الارتباط الذاتي المكاني.

ببساطة، إنها طريقة لقياس مدى قرب تجمع القيم في الفضاء ثنائي الأبعاد. غالبًا ما يتم استخدامه في الجغرافيا وعلوم المعلومات الجغرافية (GIS) لقياس مدى قرب تجميع الميزات المختلفة على الخريطة، مثل دخل الأسرة ومستوى التعليم وما إلى ذلك.

موران أنا: الصيغة

صيغة حساب Moran’s I هي:

أنا = (N/W)*ΣΣw _Ij (x _i – x )(x _j – x )/Σ(x _i – x ) ²

ذهب:

• N: عدد الوحدات المكانية المفهرسة بواسطة i و j
• W: مجموع كل _ث
• x: متغير الفائدة (دخل الأسرة، سنوات الدراسة، الخ)
• x : متوسط x
• w _j : مصفوفة الأوزان المكانية

ربما لن تضطر أبدًا إلى حساب هذا القياس يدويًا نظرًا لأن معظم البرامج الإحصائية يمكنها حسابه لك، ولكن من المفيد معرفة الصيغة المستخدمة تحت الغطاء.

يمكن أن تتراوح قيمة Moran’s I من -1 إلى 1 حيث:

• -1: متغير الاهتمام مشتت تمامًا
• 0: متغير الفائدة مشتت بشكل عشوائي
• 1: تم تجميع متغير الفائدة بشكل مثالي

إلى جانب حساب Moran’s I، تقوم معظم البرامج الإحصائية بحساب قيمة p مقابلة يمكن استخدامها لتحديد ما إذا كانت البيانات مشتتة عشوائيًا أم لا.

يستخدم اختبار موران الفرضيات الصفرية والبديلة التالية:

الفرضية الصفرية (H ₀ ): يتم تفريق البيانات بشكل عشوائي.

الفرضية البديلة ( _HA ): لا يتم توزيع البيانات عشوائيًا، أي أنها مجمعة في أنماط مرئية.

إذا كانت القيمة p التي تتوافق مع Moran’s I أقل من مستوى معين من الأهمية (أي α = 0.05)، فيمكننا رفض فرضية العدم ونستنتج أن البيانات مجمعة مكانيًا بحيث من غير المرجح أن يتم تجميعها مكانيًا. حدث بالصدفة.

موران الأول: بعض الأمثلة

تمثل الأمثلة التالية بطاقات خاطئة ذات قيم مختلفة لـ Moran’s I.

لنفترض أن كل مربع على الخريطة يمثل مقاطعة، وأن المقاطعات التي يزيد متوسط دخل الأسرة فيها عن 50000 دولار تظهر باللون الأزرق.

Moran’s I = 0: متوسط دخل الأسرة منتشر بشكل عشوائي (أي مجموعات عشوائية في مناطق عشوائية).

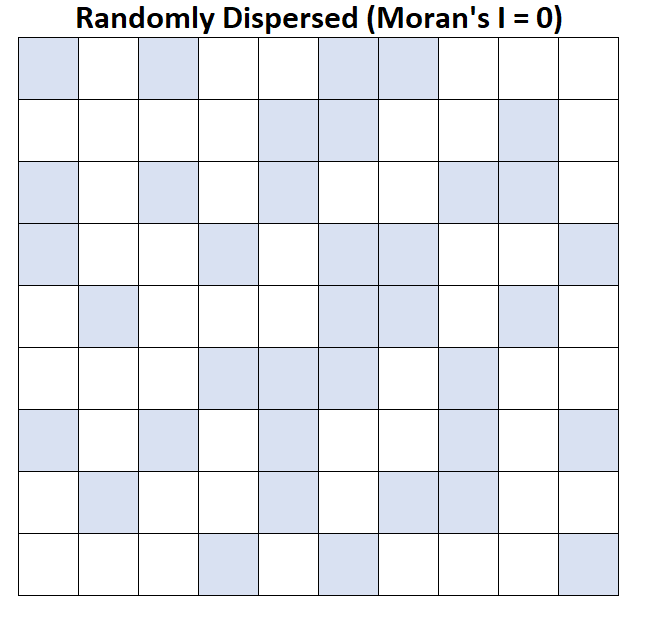
Moran’s I = -1: متوسط دخل الأسرة منتشر بشكل كامل.

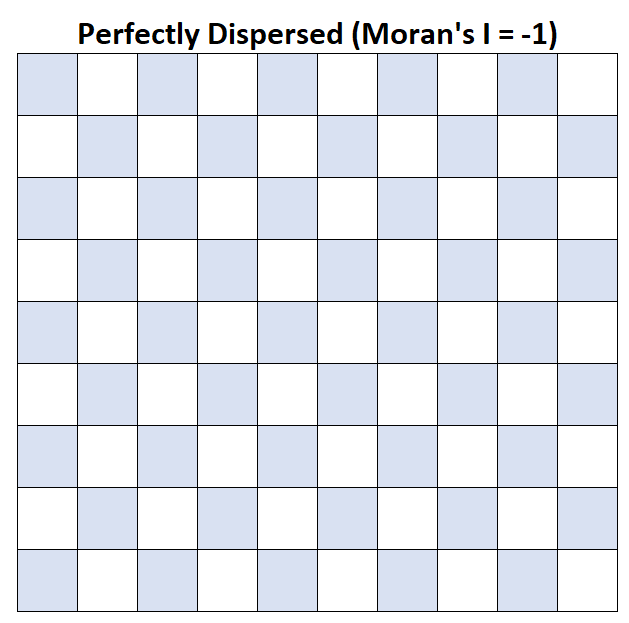
Moran’s I = 1: تم تجميع متوسط دخل الأسرة بشكل مثالي.

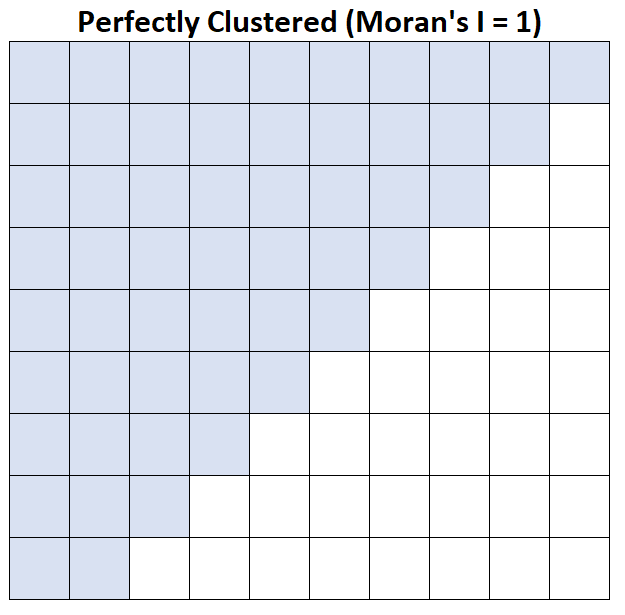
ارجع إلى هذا المثال للحصول على مثال ملموس لحساب Moran’s I في البرنامج الإحصائي R.