مؤامرة مبعثر

تشرح هذه المقالة ما هي المؤامرات المبعثرة. لذلك سوف تكتشف الغرض من استخدام السحابة النقطية، وكيفية إنشاء سحابة نقطية، وكيفية تفسيرها، وأمثلة على السحب النقطية.

ما هي سحابة النقطة؟

مخطط التشتت أو مخطط التشتت هو نوع من المخططات الإحصائية التي يتم فيها رسم مجموعة بيانات مكونة من متغيرين على محوري الإحداثيات الديكارتية.

ولذلك، يتم استخدام المخططات المبعثرة لتحليل العلاقة بين متغيرين إحصائيين.

مخططات التشتت لها عدة أسماء مختلفة، مثل مخطط الارتباط أو مخطط التشتت .

تجدر الإشارة إلى أن المخطط المبعثر يعتبر أحد الأدوات الأساسية لمراقبة الجودة، مثل مخطط باريتو ومخطط السبب والنتيجة والمخطط الانسيابي وغيرها.

كيفية عمل مخطط مبعثر

لإنشاء مخطط مبعثر، عليك اتباع الخطوات التالية:

1. جمع البيانات الإحصائية من العينة التي تريد تحليلها. ضع في اعتبارك أنه لإنشاء مخطط مبعثر، يجب أن يكون هناك متغيرين كميين على الأقل.
2. ارسم محوري المخطط المبعثر.
3. حدد المتغيرين الإحصائيين اللذين سيتم رسمهما بيانيا.
4. معايرة مقياس كل محور من محاور الرسم البياني. للقيام بذلك، يوصى أولاً بالعثور على الحد الأدنى والحد الأقصى لكل متغير، وبناءً على هذه القيم، قم بقياس كل محور.
5. قم بتمثيل كل زوج من البيانات على مخطط التشتت بنقطة.
6. تحليل وتفسير المخطط المبعثر الذي تم الحصول عليه.

مثال على مخطط التشتت

وبعد الاطلاع على تعريف المخطط المبعثر ونظرية إنشائه، يمثل هذا القسم مخططًا لهذا النوع كمثال.

• في الجدول التكراري التالي، تم جمع درجات الرياضيات والإحصاء لعينة مكونة من 20 طالبا كبيانات. رسم مجموعة البيانات على مخطط التشتت وتحليلها.

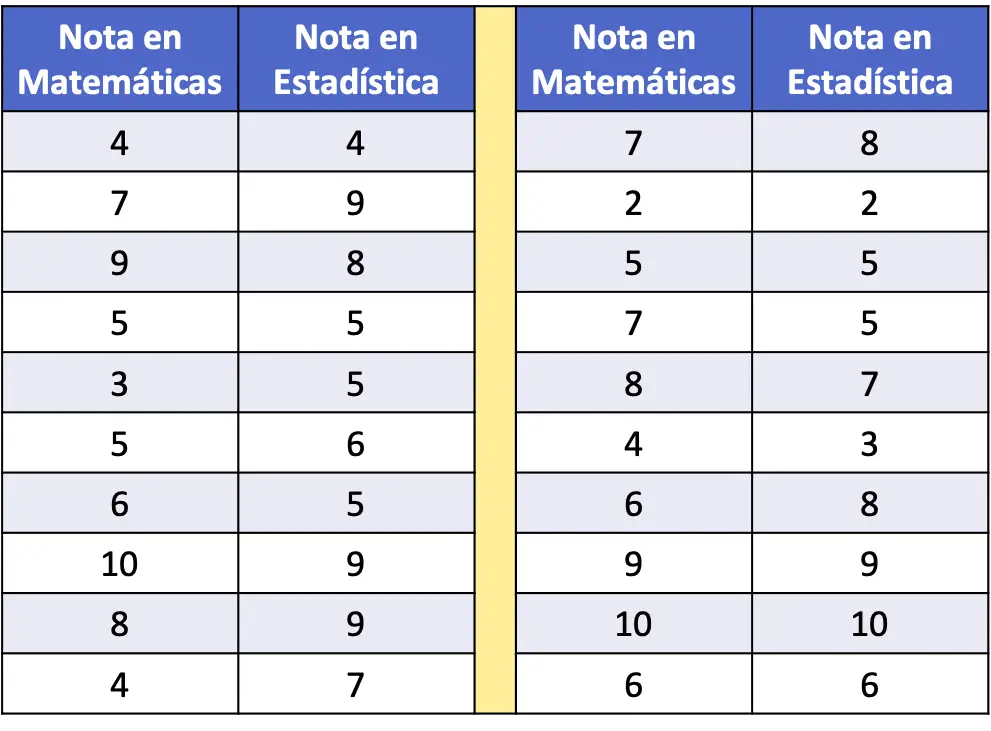
لتمثيل سلسلة البيانات في مخطط مبعثر، نحتاج ببساطة إلى رسم محورين ومعايرتهما ورسم نقطة على الرسم البياني لكل زوج من البيانات. تذكر أنه يتم وضع نقطة على الرسم البياني عند تقاطع الخطوط التخيلية المقابلة لكل قيمة من قيمها.

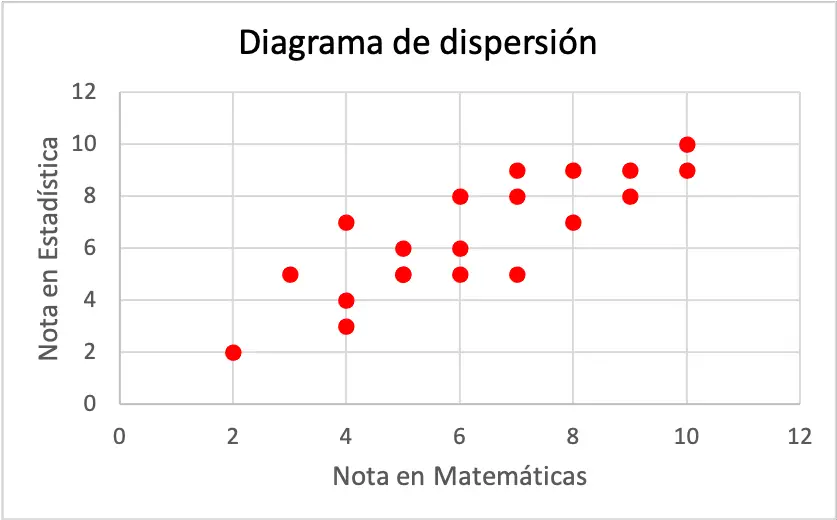
يمثل كل محور من محاور التشتت متغيرًا. وبتعبير أدق، ينتمي المحور الأفقي إلى الدرجة التي تم الحصول عليها في الرياضيات، ومن ناحية أخرى، يتوافق المحور الرأسي مع الدرجة التي تم الحصول عليها في الإحصاء.

كما ترون من مخطط التشتت، فإن المتغيرين لهما علاقة إيجابية، لأن أحد المتغيرين يزداد مع زيادة المتغير الآخر أيضًا. لذلك، نستنتج أنه إذا حصل الطالب على درجة أفضل في الرياضيات، فمن المرجح أن يحصل أيضًا على درجة أفضل في الإحصاء، والعكس صحيح.

إلا أن الاستنتاج السابق لا يعني أن أحد المتغيرين هو سبب الآخر، لأن الحصول على درجة جيدة في الرياضيات لا يضمن تلقائيا الحصول على درجة جيدة في الإحصاء دون القيام بأي شيء، بل ينبغي دراسة كلا المادتين. وفي القسم التالي سنتناول المزيد من التفاصيل حول هذا المفهوم.

مؤامرة مبعثر والارتباط

من الممكن من خلال المخطط المبعثر تحديد نوع الارتباط بين متغيرين:

• الارتباط المباشر (أو الارتباط الإيجابي) : يزداد أحد المتغيرين عندما يزيد الآخر أيضًا.
• الارتباط العكسي (أو الارتباط السلبي) : عندما يزيد أحد المتغيرين ينخفض الآخر، والعكس إذا انخفض أحد المتغيرين يزيد الآخر.
• الارتباط الصفري (لا يوجد ارتباط) : لا توجد علاقة بين المتغيرين.

وبالمثل، سواء كان الارتباط بين المتغيرين مباشرًا أو عكسيًا، فيمكن أيضًا تصنيف الارتباط بناءً على قوة أو ضعف العلاقة بين المتغيرين.

• ارتباط قوي: يرتبط المتغيران ارتباطًا وثيقًا. يتم جمع النقاط معًا على سحابة النقطة. وهذا يجعل من السهل تحديد العلاقة بين المتغيرات.
• ارتباط منخفض : توجد علاقة بين المتغيرين ولكن من الصعب تحديدها. النقاط بعيدة عن بعضها البعض على السحابة النقطية.

من ناحية أخرى، يمكن أيضًا حساب الارتباط رقميًا باستخدام صيغة، مما يسمح لك بمعرفة مدى ارتباط متغيرين مختلفين رياضيًا. لمعرفة كيفية العمل اضغط على الرابط التالي:

وتذكر أنه حتى لو كان هناك ارتباط بين متغيرين، فهذا لا يعني أن هناك علاقة سببية بينهما، أي أن الارتباط بين متغيرين لا يعني أن التغير في أحد المتغيرين هو سبب التغير في الآخر. عامل.

لذلك، مثل مخطط التشتت في القسم السابق، على الرغم من وجود علاقة إيجابية بين درجة الرياضيات ودرجة الإحصاء، إلا أن الحصول على درجة جيدة في الرياضيات لا يعني الحصول على درجة جيدة في الإحصاء، لأنك إذا درست الرياضيات فقط، فسوف تفشل بالتأكيد في الإحصائيات. ولذلك، فإن المتغيرين مرتبطان ولكنهما ليسا سببا ونتيجة.

ولمعرفة المزيد يمكنك متابعة التدوينة التالية:

مزايا وعيوب سحابة النقطة

نظرًا لخصائص مخطط التشتت، فإن هذا النوع من المخططات الإحصائية له مزايا وعيوب.

ميزة:

• من السهل جدًا تمثيل سلسلة من البيانات على مخطط مبعثر.
• يسمح لك مخطط التشتت بتحليل العلاقة بين متغيرين بشكل مرئي، مما يسهل استخلاص النتائج.
• يمكن أيضًا استخدام مخططات التشتت في دراسة إحصائية متعمقة كاستكشاف أولي للبيانات.

سلبيات:

• هذه الأنواع من الرسوم البيانية ليست مفيدة لتمثيل المتغيرات النوعية.
• يمكن أن يؤدي تفسير المخطط المبعثر إلى استنتاج خاطئ للسبب والنتيجة بين متغيرين.
• لا تسمح لك مخططات التشتت بتحليل العلاقة بين أكثر من متغيرين.