مربع والخط الطولي مؤامرة
تشرح هذه المقالة ماهية boxplot، والمعروفة أيضًا باسم boxplot (أو boxplot). سوف تكتشف كيفية إنشاء هذه الأنواع من الرسوم البيانية الإحصائية، كما ستكتشف تمرينًا محلولاً للمخطط المربع والشريطي وتفسيره.
ما هو مربع ومؤامرة الطولي؟
Boxplot ، ويسمى أيضًا boxplot أو boxplot ، هو رسم بياني يمثل بشكل مرئي مجموعة من البيانات الإحصائية باستخدام الأرباع.
السمة الرئيسية لمؤامرة الصندوق والشريط هي أنها تسمح لك بتصور تشتت سلسلة من البيانات بسرعة، لأنها تشير إلى الربعيات والوسيط والقيم المتطرفة والقيم المتطرفة للبيانات.
وبالتالي فإن هذا النوع من المخططات يتكون من مربع مستطيل وبضعة أسطر (أو شعيرات) تخرج منها القيم التالية:
- تشير حدود الصندوق إلى الربعين الأول والثالث (س 1 و س 3 ). والخط العمودي داخل الصندوق هو الوسيط (أي ما يعادل الربع الثاني Q2 ).
- حدود الشعيرات (أو الأذرع) هي القيم المتطرفة ، أي القيمة الدنيا والقيمة القصوى لسلسلة البيانات.
- النقاط الموجودة خارج الشعيرات هي قيم متطرفة ، أو بمعنى آخر، البيانات التي ربما تم قياسها بشكل غير صحيح ، وبالتالي لا ينبغي أن تؤخذ في الاعتبار في الدراسة الإحصائية.
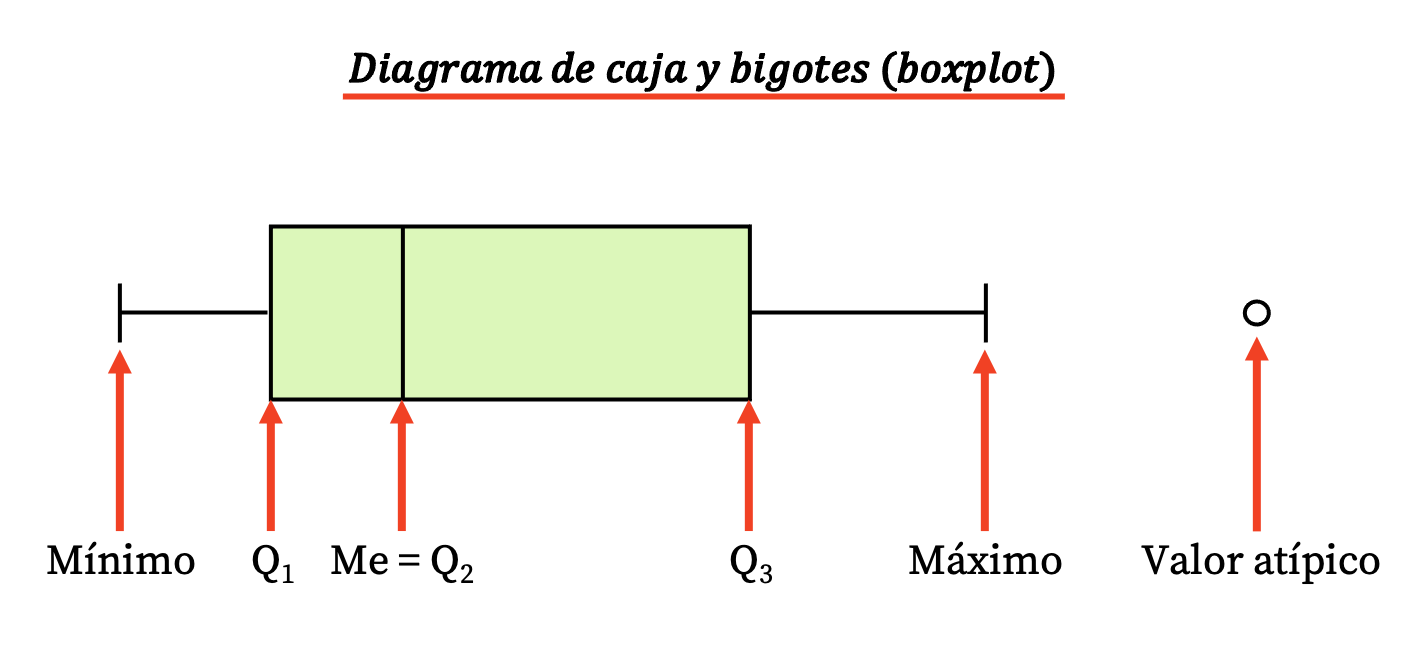
لاحظ أن الفرق بين الربعين الثالث والأول هو النطاق الربيعي (أو المدى الربيعي)، وهو مقياس آخر للتشتت الإحصائي.
تعتبر المخططات الصندوقية والشعيرات مفيدة جدًا لمقارنة المتغيرات العددية. ومع ذلك، فهو غير مناسب لتمثيل المتغيرات الفئوية.
كيفية إنشاء مربع ومؤامرة شارب
لإنشاء مخطط مربع وطرفي (أو مخطط مربع) من سلسلة بيانات، يجب تنفيذ الخطوات التالية:
- فرز أمثلة البيانات الإحصائية.
- احسب الأرباع (Q 1 و Q 2 و Q 3 ) ومثلها بالمربع في الرسم التخطيطي. يتوافق الربعان الأول والثالث مع حدود الصندوق، ولتمثيل الوسيط (الربيع الثاني) يجب عليك رسم خط داخل الصندوق حيث تقع قيمته.
- احسب المدى الربيعي الذي يساوي الربيع الثالث ناقص الربيع الأول.
- احسب القيم المسموح بها LI وLS، وصيغها هي:
- تحديد القيم المتطرفة للعينة، وهي قيم أقل من LI أو أكبر من LS. قم بتمثيل هذه القيم خارج نطاق الطولي بالنقاط.
- تحديد وتمثيل القيم القصوى، وهي أصغر قيمة وأكبر قيمة في الفترة التي شكلتها LI وLS. تمثل هذه القيم نهاية الشاربين في الرسم التخطيطي.
![]()
![]()
![]()
مثال على مؤامرة الصندوق والشارب
بالنظر إلى تعريف ونظرية المخطط الصندوقي والشريطي (أو المخطط المربع)، ستجد أدناه مثالًا ملموسًا لفهم المفهوم بشكل أفضل ومعرفة كيفية تنفيذ هذا النوع من المخططات الإحصائية.
- ارسم مخططًا مربعًا لمجموعة البيانات الإحصائية التالية.

في هذه الحالة، يتم ترتيب البيانات بالفعل من الأصغر إلى الأكبر، لذا لا يلزم إجراء أي تغييرات. بخلاف ذلك، يجب علينا فرز بيانات العينة أولاً.
ثانياً: نستخرج رباعيات العينة:
![]()
![]()
![]()
بمجرد قيامنا بحساب الربيعيات الثلاثة، نجد المدى الربيعي عن طريق طرح الربع 3 ناقص الربع 1:
![]()
نقوم الآن بحساب حدود LI وLS، وهي القيم التي تعتبر البيانات منها غير نمطية. للقيام بذلك، يجب عليك استخدام الصيغ التالية:
![]()
![]()
إذن في هذه الحالة لدينا قيمتان متطرفتان، لأن 3.02 أقل من 3.16 و5.71 أكبر من 5.56.
![]()
أخيرًا، يبقى تحديد القيم المتطرفة، وهي الحد الأدنى والحد الأقصى لجميع البيانات الموجودة في الفاصل الزمني [LI,LS]. ولذلك، في مثالنا، الحد الأدنى للقيمة هو 3.70 والحد الأقصى للقيمة هو 4.81.
![]()
![]()
لذا، بمجرد أن حددنا جميع قيم الصندوق والمخطط الطولي، كل ما يتبقى هو إجراء التمثيل الرسومي:
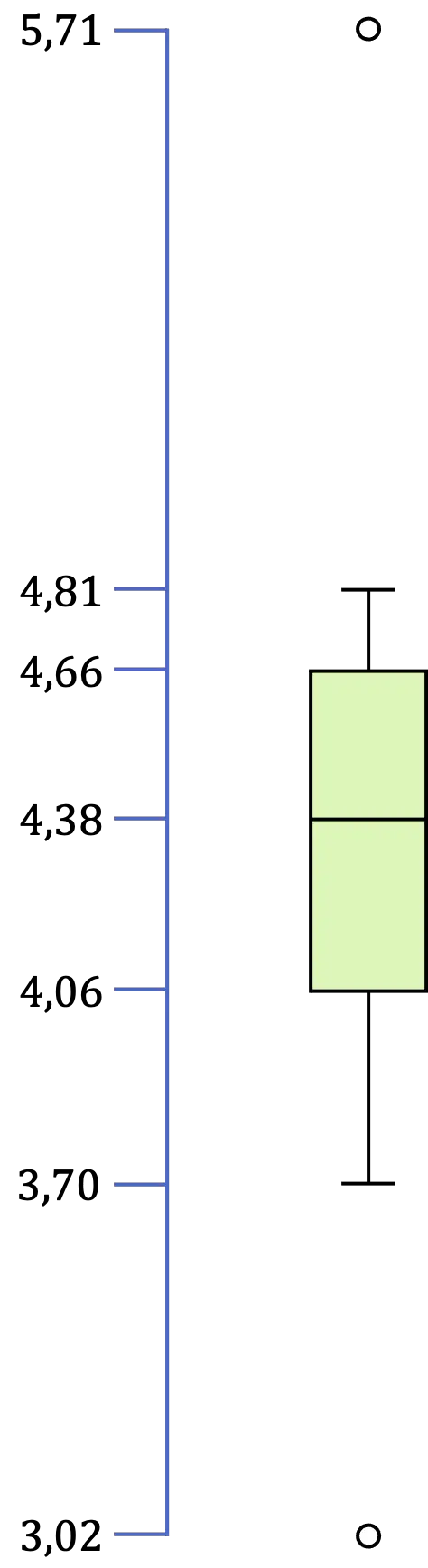
ما هي قطعة الأرض المستخدمة في الصندوق والشعيرات؟
أخيرًا، دعونا نرى الغرض منه وكيفية تفسير مؤامرة الصندوق والطول (أو مؤامرة الصندوق).
من الواضح أن مخطط الصندوق والشريط مفيد جدًا لمعرفة الربعيات والمدى الربيعي والوسيط والقيم المتطرفة والقيم المتطرفة لسلسلة البيانات بسرعة، حيث يمكن تحديد كل هذه القياسات الإحصائية بنظرة بسيطة.
بالإضافة إلى ذلك، يتم استخدام مخطط الصندوق والشريط الطولي لتحليل تماثل العينة الإحصائية، لأنه يمثل بصريًا مجموعة البيانات بأكملها. إذا لم يكن الوسيط في وسط الصندوق، فهذا يعني أن العينة غير متماثلة.
وبالمثل، تُستخدم boxplots على نطاق واسع في سوق الأوراق المالية لتمثيل التباين في سعر السهم خلال فترة زمنية، لأنها تسمح للشخص برؤية القيمة القصوى والحد الأدنى للقيمة والقيم المتوسطة في فترة زمنية قصيرة. الوقت وبالتالي اتخاذ قرارات أسرع.