نسبة الأرجحية المعدلة: التعريف + الأمثلة

في الإحصاء، تخبرنا نسبة الأرجحية عن النسبة بين احتمال وقوع حدث في مجموعة العلاج واحتمال وقوع حدث في مجموعة المراقبة.

تظهر نسب الأرجحية بشكل شائع في الانحدار اللوجستي ، وهي طريقة نستخدمها لتناسب نموذج الانحدار الذي يحتوي على واحد أو أكثر من متغيرات التنبؤ ومتغير الاستجابة الثنائية.

نسبة الأرجحية المعدلة هي نسبة الأرجحية التي تم تعديلها لمتغيرات التوقع الأخرى في النموذج.

إنه مفيد بشكل خاص في مساعدتنا على فهم كيفية تأثير متغير التوقع على فرص وقوع حدث ما، بعد ضبط تأثير متغيرات التوقع الأخرى.

يوضح المثال التالي الفرق بين نسبة الأرجحية ونسبة الأرجحية المعدلة.

مثال: حساب نسب الأرجحية المعدلة

لنفترض أننا نريد أن نفهم ما إذا كان عمر الأم يؤثر على احتمالية إنجاب طفل منخفض الوزن عند الولادة.

لاستكشاف ذلك، يمكننا إجراء الانحدار اللوجستي باستخدام العمر كمتغير متوقع وانخفاض الوزن عند الولادة (نعم أو لا) كمتغير الاستجابة .

لنفترض أننا قمنا بجمع بيانات عن 300 أم ونتناسب مع نموذج الانحدار اللوجستي. وهنا النتائج:

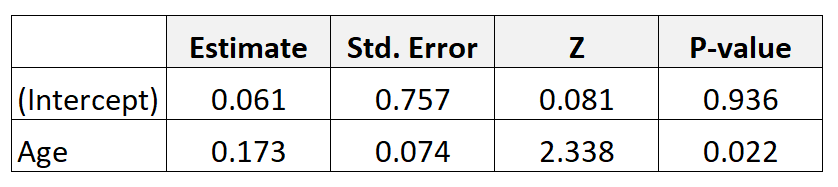
للحصول على نسبة الأرجحية للعمر، ما عليك سوى مضاعفة تقدير المعامل من الجدول: e ^0.173 = 1.189 .

ويخبرنا هذا أن زيادة العمر لمدة عام واحد ترتبط بزيادة قدرها 1,189 في احتمالات انخفاض وزن الطفل عند الولادة. بمعنى آخر، تزداد فرص إنجاب طفل منخفض الوزن عند الولادة بنسبة 18.9% لكل زيادة سنوية إضافية في العمر.

تسمى نسبة الأرجحية هذه نسبة الأرجحية “الخام” أو نسبة الأرجحية “غير المعدلة” لأنه لم يتم تعديلها لمتغيرات التوقع الأخرى في النموذج لأنها المتغير التوقع الوحيد في النموذج.

ولكن لنفترض أننا نريد أن نفهم ما إذا كان عمر الأم وعادات التدخين تؤثر على احتمالية إنجاب طفل منخفض الوزن عند الولادة.

لاستكشاف ذلك، يمكننا إجراء الانحدار اللوجستي باستخدام العمر والتدخين (نعم أو لا) كمتغيرات تنبؤية وانخفاض الوزن عند الولادة كمتغير الاستجابة .

لنفترض أننا قمنا بجمع بيانات عن 300 أم ونتناسب مع نموذج الانحدار اللوجستي. وهنا النتائج:

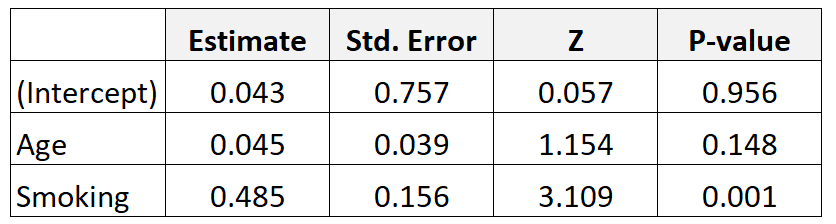
وإليك كيفية تفسير النتائج:

العمر: يتم حساب نسبة الأرجحية المعدلة حسب العمر على النحو التالي: ه ^0.045 = 1.046 . وهذا يعني أن فرص إنجاب طفل منخفض الوزن عند الولادة تزيد بنسبة 4.6% لكل زيادة سنوية إضافية في العمر، على افتراض بقاء متغير التدخين ثابتا.

على سبيل المثال، لنفترض أن الأم أ والأم ب كلاهما يدخنان. إذا كانت الأم “أ” أكبر من الأم “ب” بسنة واحدة، فإن احتمال أن تنجب الأم “أ” طفلًا منخفض الوزن عند الولادة هو 1.046 ضعف احتمال أن تنجب الأم “ب” طفلًا منخفض الوزن عند الولادة.

التدخين : يتم حساب نسبة الأرجحية المعدلة للتدخين على النحو التالي: ^e.485 = 1.624 . وهذا يعني أن فرص إنجاب طفل منخفض الوزن عند الولادة ترتفع بنسبة 62.4% إذا كانت الأم مدخنة (مقارنة بعدم التدخين)، على افتراض بقاء متغير العمر ثابتا.

على سبيل المثال، لنفترض أن الأم أ والأم ب يبلغان من العمر 30 عامًا. إذا كانت الأم “أ” تدخن أثناء الحمل والأم “ب” لا تدخن، فإن فرص إنجاب الأم “أ” لطفل منخفض الوزن عند الولادة تكون أعلى بنسبة 62.4% من فرص إنجاب الأم “ب” لطفل منخفض الوزن عند الولادة.

لاحظ أن نسبة الأرجحية المعدلة حسب العمر أقل من نسبة الأرجحية غير المعدلة من المثال السابق. وذلك لأنه عندما تزيد متغيرات التوقع الأخرى من فرص حدوث متغير الاستجابة، فإن نسبة الأرجحية المعدلة لمتغير التوقع الموجود بالفعل في النموذج ستنخفض دائمًا.

ملخص: نسبة الأرجحية مقابل نسبة الأرجحية المعدلة

تعتبر نسبة الأرجحية (التي تسمى أحيانًا نسبة الأرجحية “الخامة”) مفيدة في إخبارنا كيف تؤثر التغييرات في متغير التوقع على فرص حدوث متغير الاستجابة.

تعتبر نسبة الأرجحية المعدلة مفيدة في إخبارنا كيف تؤثر التغييرات في متغير التوقع على فرص حدوث متغير الاستجابة، بعد التحكم في متغيرات التوقع الأخرى في النموذج.

مصادر إضافية

مقدمة في الانحدار اللوجستي
كيفية إجراء الانحدار اللوجستي في R
كيفية تنفيذ الانحدار اللوجستي في بايثون