كيفية تطبيق نظرية الحد المركزي على الآلة الحاسبة ti-84

تنص نظرية الحد المركزي على أن توزيع المعاينة لمتوسط العينة يكون طبيعيًا تقريبًا إذا كان حجم العينة كبيرًا بدرجة كافية، حتى لو كان توزيع السكان غير طبيعي.

تنص نظرية الحد المركزي أيضًا على أن توزيع العينات سيكون له الخصائص التالية:

1. سيكون متوسط توزيع العينة مساوياً لمتوسط توزيع السكان:

س = μ

2. سيكون الانحراف المعياري لتوزيع العينة مساوياً للانحراف المعياري للسكان مقسوماً على حجم العينة:

ق = σ / √ن

للعثور على الاحتمالات المتعلقة بمتوسط العينة على الآلة الحاسبة TI-84، يمكننا استخدام الدالة Normalcdf() بالصيغة التالية:

 normalcdf (lower value, upper value, x , s/√ n )

ذهب:

• x : متوسط العينة
• s : عينة الانحراف المعياري
• ن : حجم العينة

للوصول إلى هذه الوظيفة على الآلة الحاسبة TI-84، ما عليك سوى الضغط على الرقم 2 ثم الضغط على VARS ثم التمرير إلى Normalcdf ( واضغط على ENTER) .

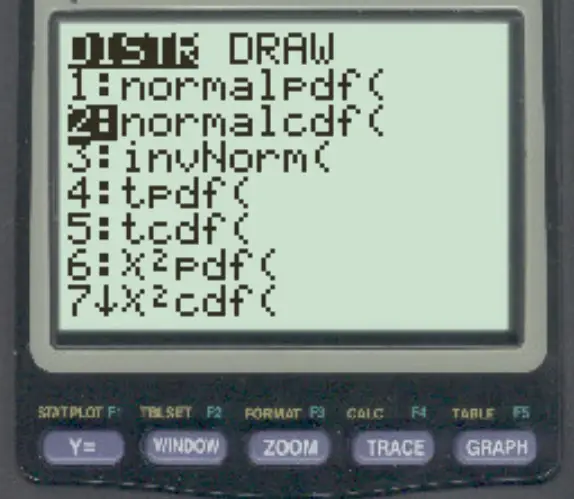
توضح الأمثلة التالية كيفية استخدام هذه الوظيفة عمليًا.

مثال 1: أوجد الاحتمال بين قيمتين

توزيع له متوسط 70 وانحراف معياري 7. إذا اخترنا عينة عشوائية حجمها n = 35، فأوجد احتمال أن يكون متوسط العينة بين 68 و72.

يمكننا استخدام بناء الجملة التالي على TI-84:

 normalcdf (68, 72, 70, 7/√ 35 ) 

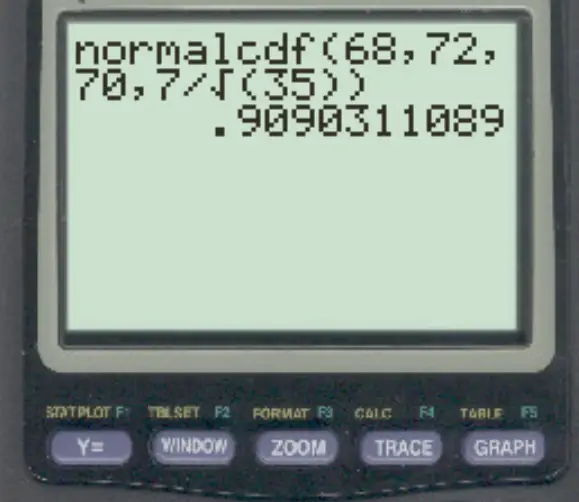
احتمال أن يكون متوسط العينة بين 68 و 72 هو 0.909 .

مثال 2: إيجاد احتمال أكبر من قيمة

توزيع له متوسط 50 وانحراف معياري 4. إذا اخترنا عينة عشوائية حجمها n = 30، فأوجد احتمال أن يكون متوسط العينة أكبر من 48.

يمكننا استخدام بناء الجملة التالي على TI-84:

 normalcdf (48, E99, 50, 4/√ 30 )

ملاحظة: يمكنك الوصول إلى الرمز “E” بالضغط على 2 ثم الضغط على الزر .

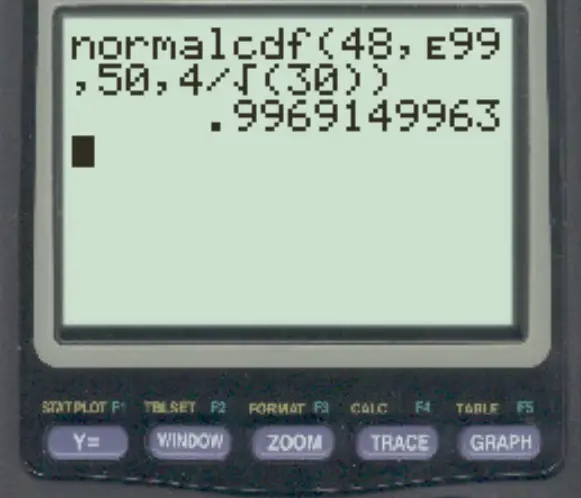
احتمال أن يكون متوسط العينة أكبر من 48 هو 0.9969 .

مثال 3: إيجاد احتمال أقل من قيمة

توزيع له متوسط 20 وانحراف معياري 3. إذا اخترنا عينة عشوائية حجمها n = 40، فأوجد احتمال أن يكون متوسط العينة أقل من 19.

يمكننا استخدام بناء الجملة التالي على TI-84:

 normalcdf (-E99, 19, 20, 3/√ 40 ) 

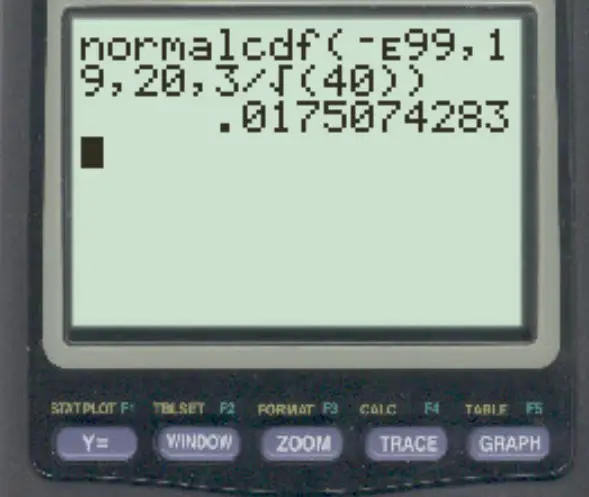
احتمال أن يكون متوسط العينة أقل من 19 هو 0.0175 .

مصادر إضافية

مقدمة لنظرية الحد المركزي
حاسبة نظرية الحد المركزي
كيفية تطبيق نظرية الحد المركزي في إكسل
نظرية الحد المركزي: الشروط الأربعة الواجب تحقيقها