كيفية تطبيق نظرية الحد المركزي في لغة r (مع أمثلة)

تنص نظرية الحد المركزي على أن توزيع المعاينة لمتوسط العينة يكون طبيعيًا تقريبًا إذا كان حجم العينة كبيرًا بدرجة كافية، حتى لو كان توزيع السكان غير طبيعي.

تنص نظرية الحد المركزي أيضًا على أن توزيع العينات سيكون له الخصائص التالية:

1. سيكون متوسط توزيع العينة مساوياً لمتوسط توزيع السكان:

س = μ

2. سيكون الانحراف المعياري لتوزيع العينة مساوياً للانحراف المعياري لتوزيع السكان مقسوماً على حجم العينة:

الصورة = σ /ن

يوضح المثال التالي كيفية تطبيق نظرية الحد المركزي في R.

مثال: تطبيق نظرية الحد المركزي في R

لنفترض أن عرض قوقعة السلحفاة يتبع توزيعًا موحدًا بحد أدنى للعرض يبلغ 2 بوصة والحد الأقصى للعرض 6 بوصات.

أي أننا إذا اخترنا سلحفاة عشوائيًا وقمنا بقياس عرض صدفتها، فمن المحتمل أيضًا أن يتراوح عرضها بين 2 و6 بوصات.

يوضح الكود التالي كيفية إنشاء مجموعة بيانات في R تحتوي على قياسات عرض الدرع لـ 1000 سلحفاة، موزعة بالتساوي بين 2 و6 بوصات:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

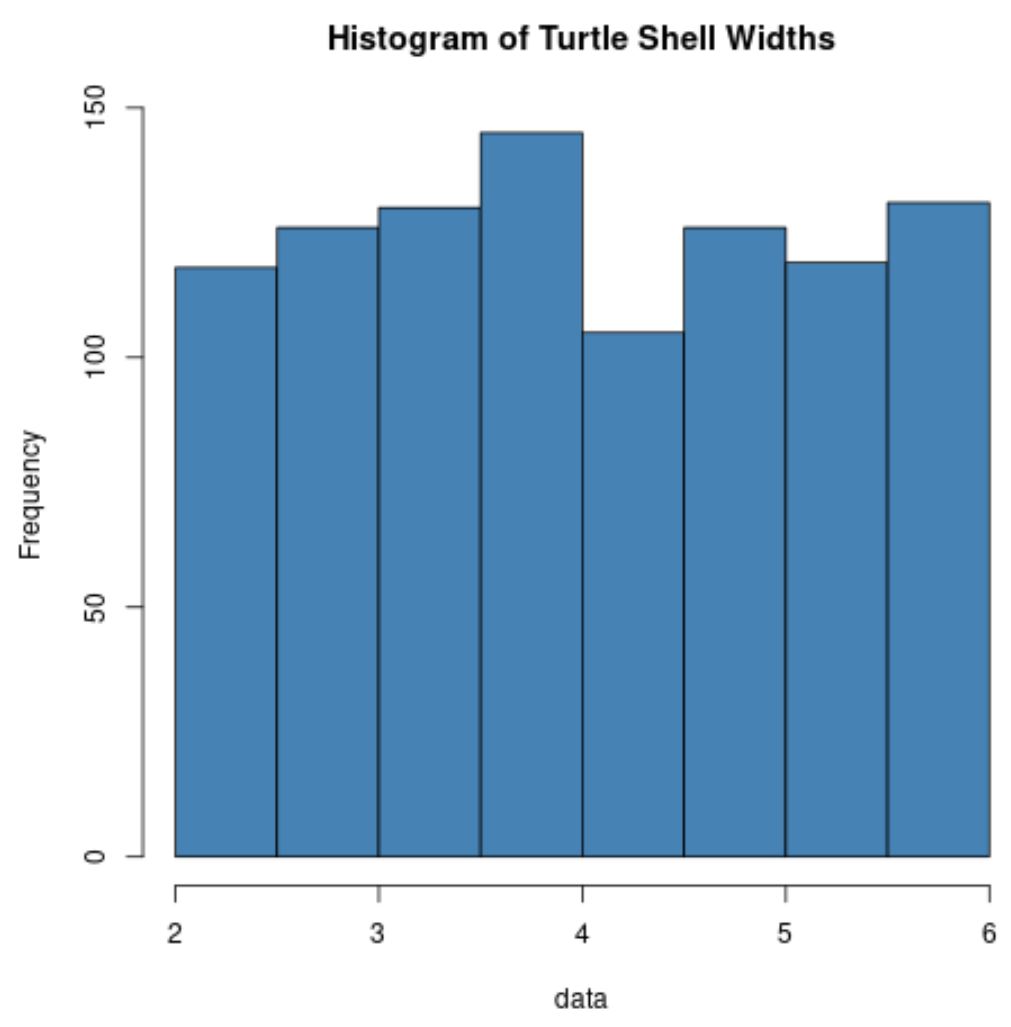
لاحظ أن توزيع عرض صدفة السلحفاة لا يتم توزيعه على الإطلاق.

تخيل الآن أننا أخذنا عينات عشوائية متكررة من 5 سلاحف من هذه المجموعة وقمنا بقياس متوسط العينة مرارًا وتكرارًا.

يوضح التعليمة البرمجية التالية كيفية القيام بهذه العملية في R وإنشاء رسم بياني لتصور توزيع وسائل العينة:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

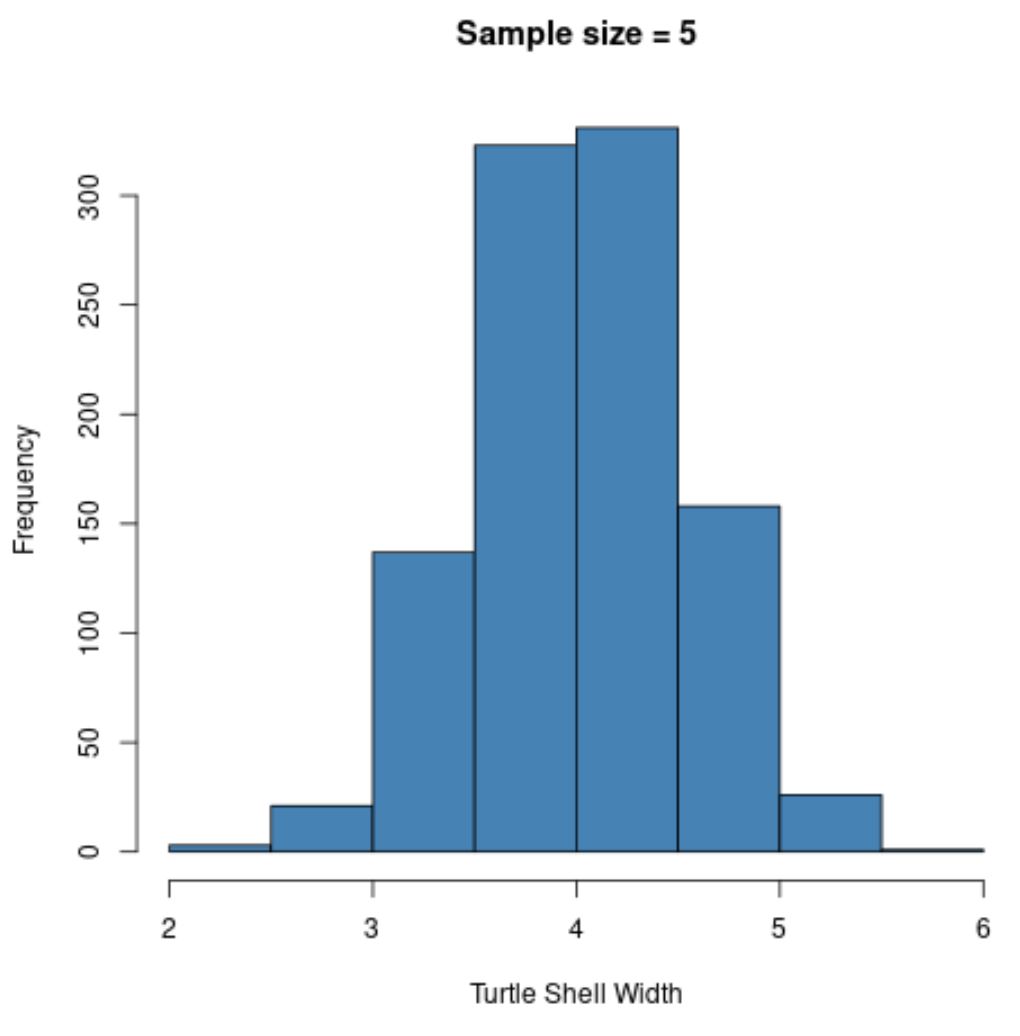
لاحظ أن توزيع المعاينة لمتوسطات العينة يبدو موزعاً بشكل طبيعي، على الرغم من أن التوزيع الذي جاءت منه العينات لم يكن موزعاً بشكل طبيعي.

لاحظ أيضًا متوسط العينة والانحراف المعياري للعينة لتوزيع العينات هذا:

• س̄ : 4.008
• ق : 0.517

لنفترض الآن أننا قمنا بزيادة حجم العينة التي نستخدمها من n=5 إلى n=30 وأعدنا إنشاء الرسم البياني لوسائل العينة:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

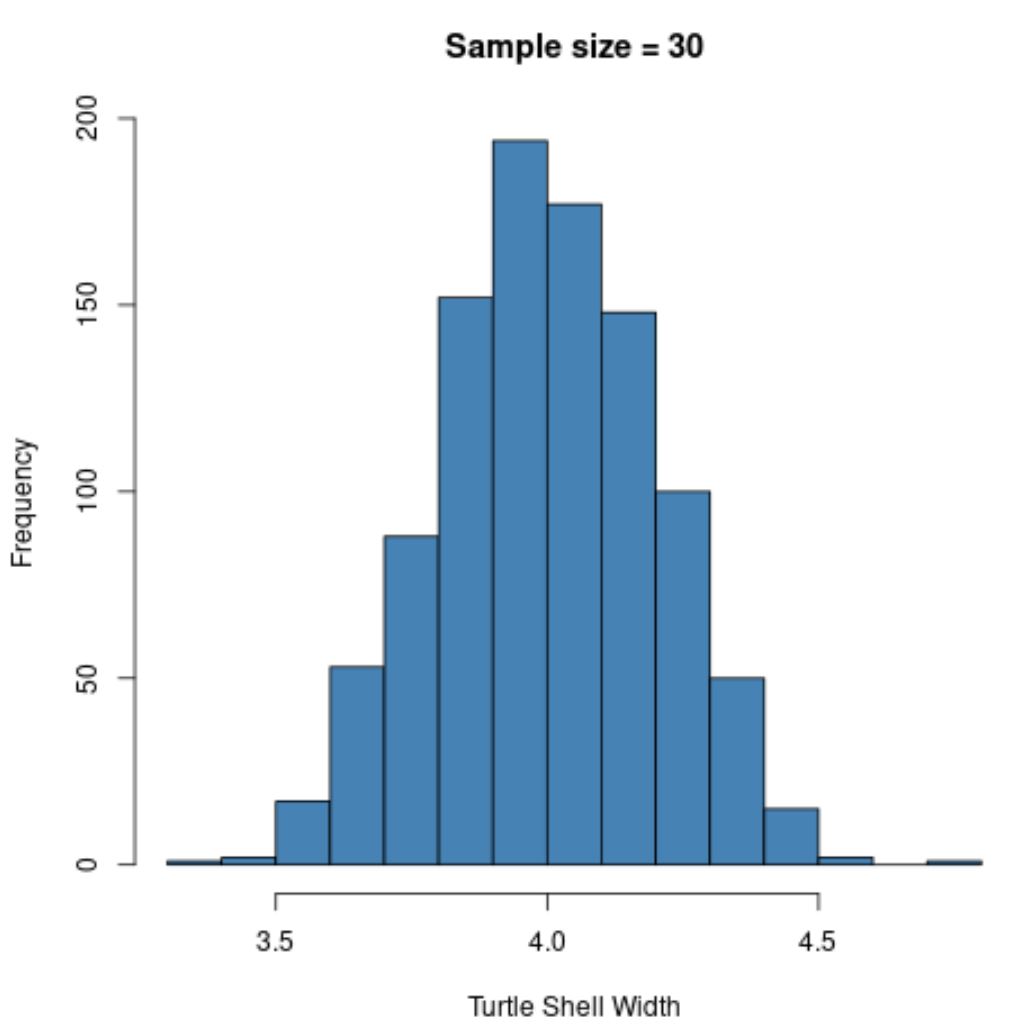
يتم توزيع توزيع العينات بشكل طبيعي مرة أخرى، ولكن الانحراف المعياري للعينة أصغر:

• ق : 0.200

وذلك لأننا استخدمنا حجم عينة أكبر (ن = 30) مقارنة بالمثال السابق (ن = 5)، وبالتالي فإن الانحراف المعياري لمتوسط العينة أصغر.

وإذا واصلنا استخدام عينات أكبر وأكبر، فسنجد أن الانحراف المعياري للعينة يصبح أصغر فأصغر.

وهذا يوضح نظرية الحد المركزي في الممارسة العملية.

مصادر إضافية

توفر الموارد التالية معلومات إضافية حول نظرية الحد المركزي:

مقدمة لنظرية الحد المركزي
حاسبة نظرية الحد المركزي
5 أمثلة لاستخدام نظرية الحد المركزي في الحياة الحقيقية