كيفية تطبيق نظرية بايز في إكسل

تنص نظرية بايز على ما يلي للحدثين A و B :

P(A|B) = P(A)*P(B|A) / P(B)

ذهب:

• P(A|B): احتمال وقوع الحدث A، بمعلومية الحدث B.
• P(B|A): احتمال وقوع الحدث B، بشرط وقوع الحدث A.
• P(A): احتمال وقوع الحدث A.
• P(B): احتمال وقوع الحدث B.

على سبيل المثال، لنفترض أن احتمال أن يكون الطقس غائما هو 40%. لنفترض أيضًا أن احتمال سقوط المطر في يوم معين هو 20% واحتمال حدوث السحب في يوم ممطر هو 85%.

إذا كان الجو غائمًا في الخارج في يوم معين، فما احتمال سقوط المطر في ذلك اليوم؟

الحل :

• ف(غائم) = 0.40
• ف(المطر) = 0.20
• P(غائم | مطر) = 0.85

وهكذا يمكننا حساب:

• P(مطر | غائم) = P(مطر) * P(غائم | مطر) / P(غائم)
• P(مطر | غائم) = 0.20 * 0.85 / 0.40
• P(مطر | غائم) = 0.425

إذا كان الجو غائمًا في الخارج في يوم معين، فإن احتمال سقوط المطر في ذلك اليوم هو 0.425 أو 42.5% .

يوضح المثال التالي كيفية حل هذه المشكلة بالضبط باستخدام نظرية بايز في Excel.

مثال: نظرية بايز في إكسل

توضح الصيغة التالية كيفية تطبيق نظرية بايز في إكسيل:

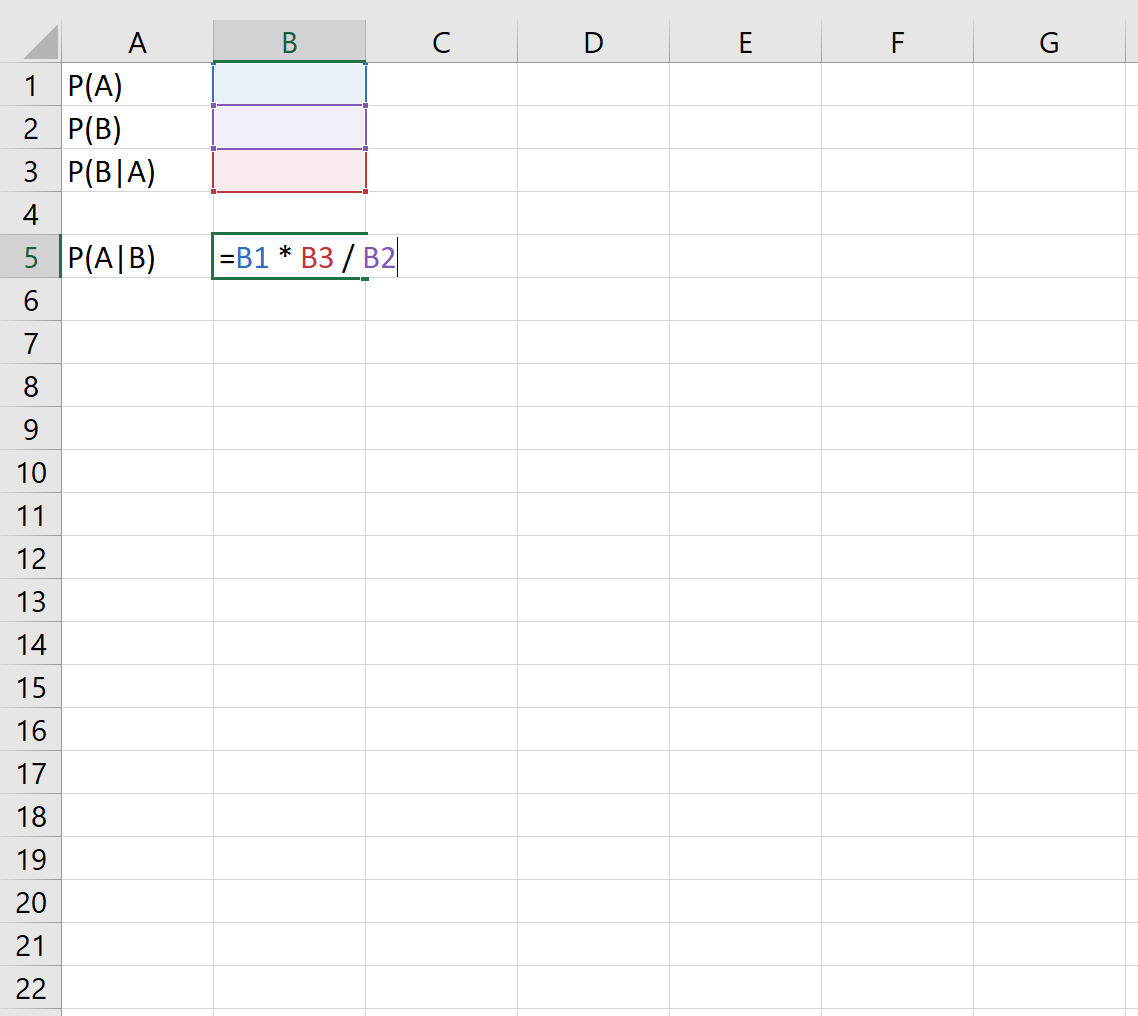
على سبيل المثال، إذا عرفنا الاحتمالات التالية:

• ف(غائم) = 0.40
• ف(المطر) = 0.20
• P(غائم | مطر) = 0.85

ثم يمكننا ببساطة توصيلها بخلايا Excel:

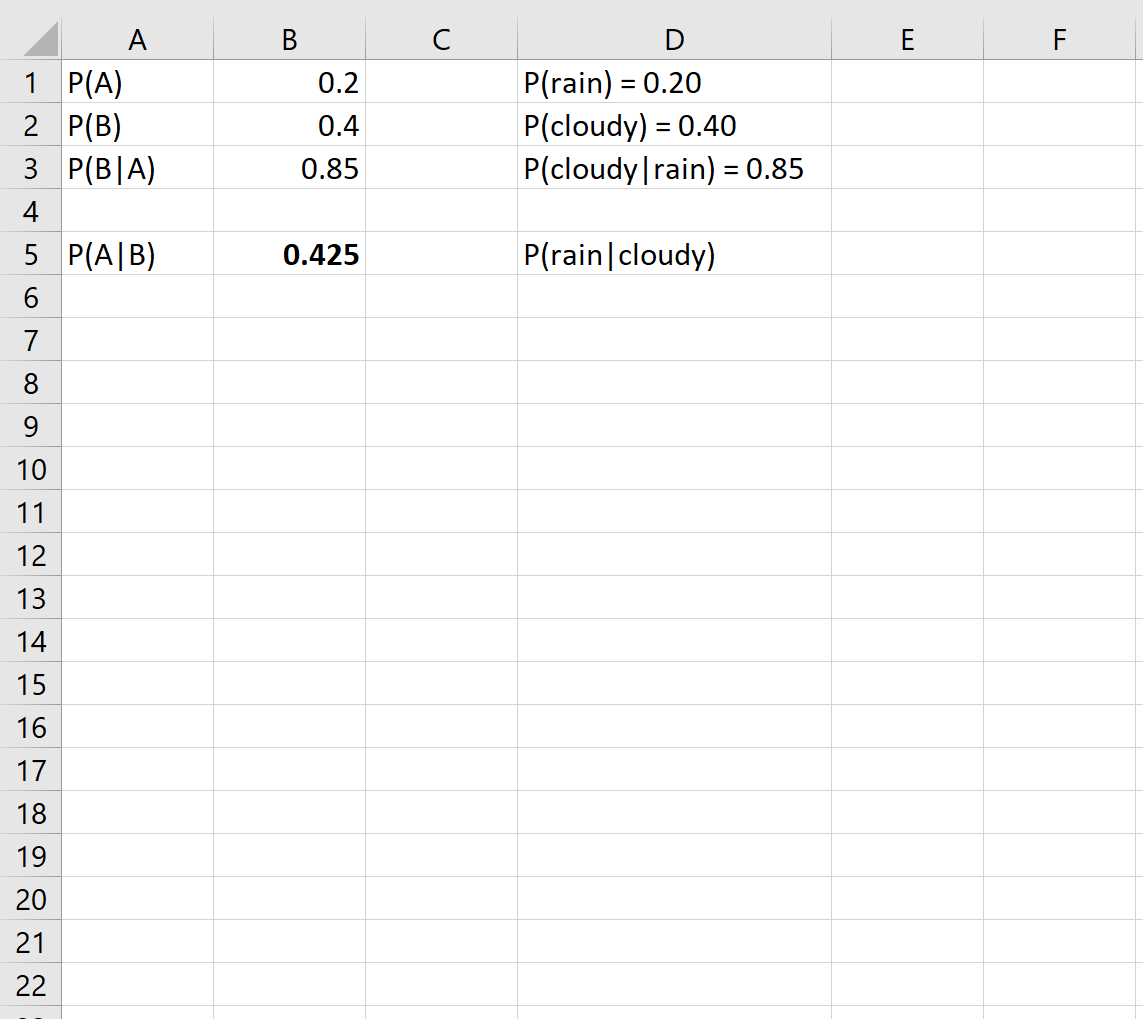
يخبرنا هذا أنه إذا كان الجو غائمًا في الخارج في يوم معين، فإن احتمال هطول الأمطار في ذلك اليوم هو 0.425 أو 42.5% .

مصادر إضافية

كيفية حساب الاحتمال الشرطي في إكسيل
كيفية تطبيق القاعدة الأساسية في Excel
كيفية تطبيق نظرية الحد المركزي في إكسل