كيفية إجراء اختبار t لعينة واحدة في excel

يتم استخدام اختبار t لعينة واحدة لاختبار ما إذا كان متوسط المجتمع يساوي قيمة معينة أم لا.

يشرح هذا البرنامج التعليمي كيفية إجراء اختبار t لعينة واحدة في Excel.

كيفية إجراء اختبار t لعينة واحدة في Excel

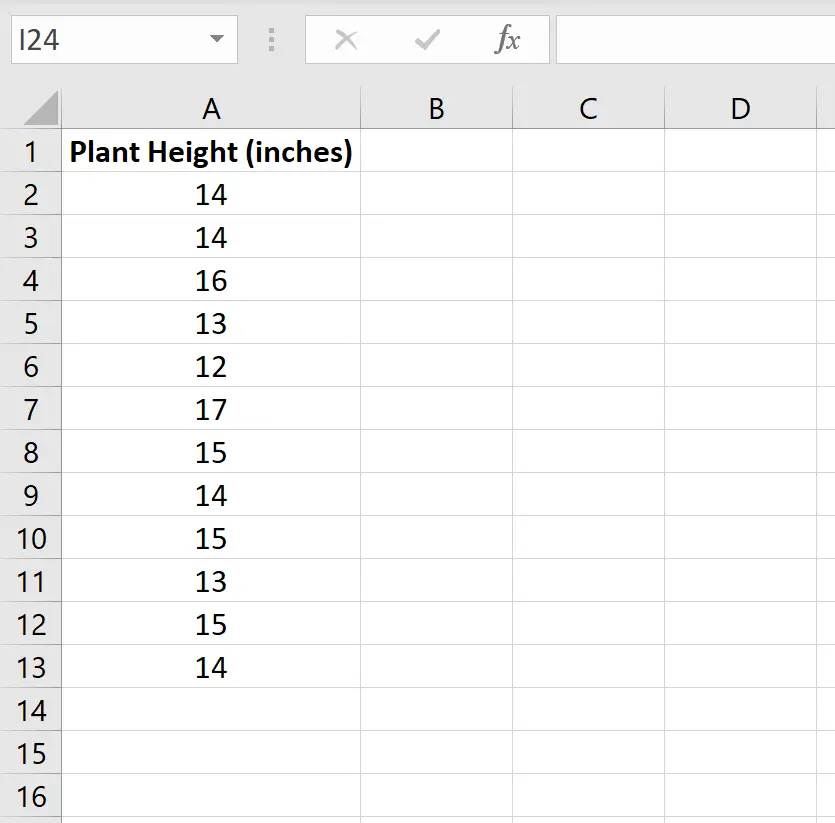
لنفترض أن عالم النبات يريد معرفة ما إذا كان متوسط ارتفاع نوع معين من النباتات يساوي 15 بوصة. أخذت عينة عشوائية من 12 نباتًا وسجلت ارتفاع كل منها بالبوصة.

الصورة التالية توضح الارتفاع (بالبوصة) لكل نبات في العينة:

يمكننا استخدام الخطوات التالية لإجراء اختبار t لعينة واحدة لتحديد ما إذا كان متوسط ارتفاع هذا النوع من النباتات هو في الواقع 15 بوصة.

الخطوة 1: ابحث عن حجم العينة ومتوسط العينة والانحراف المعياري للعينة.

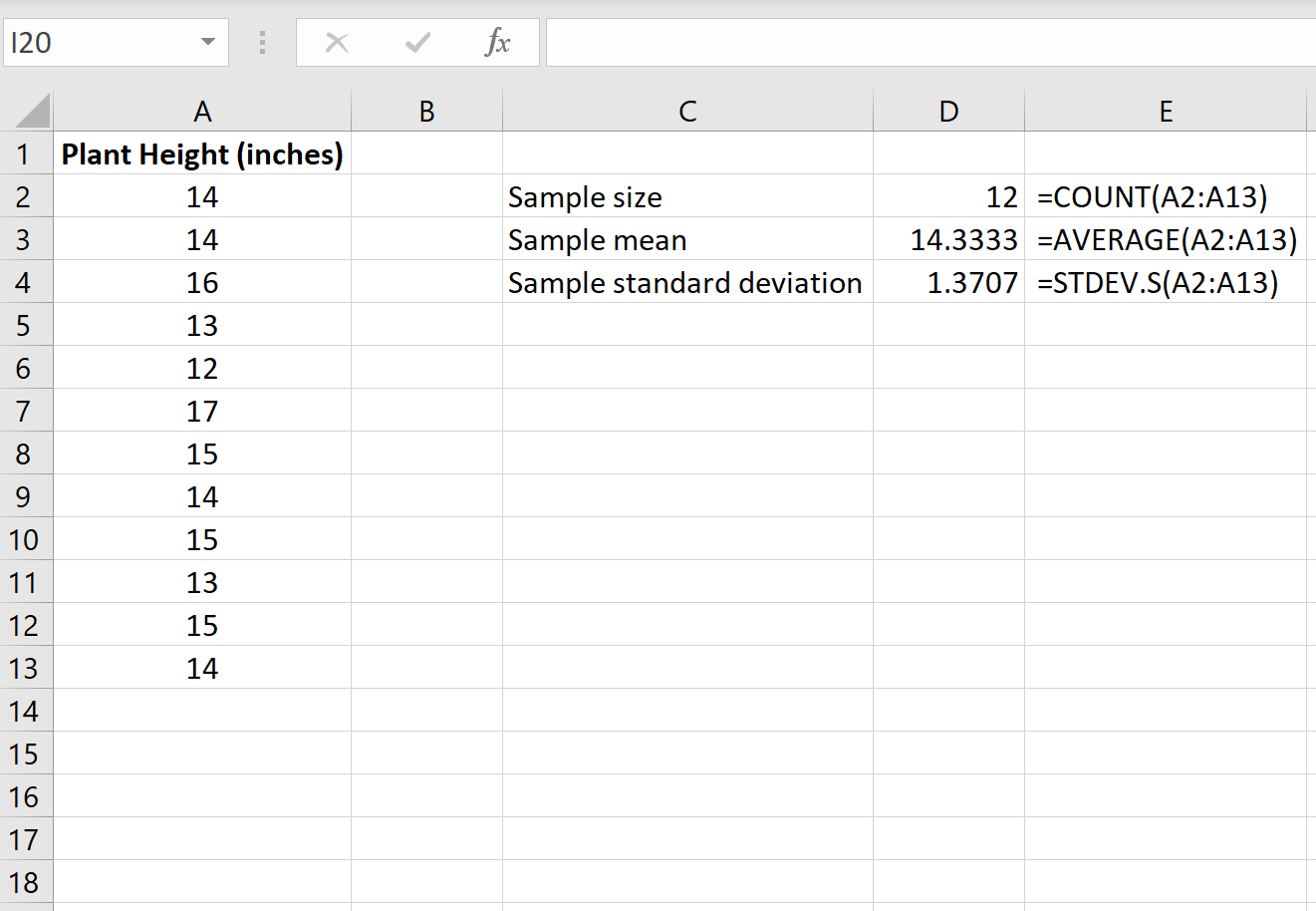
أولاً، نحتاج إلى إيجاد حجم العينة، ومتوسط العينة، والانحراف المعياري للعينة، والتي سيتم استخدامها جميعًا لإجراء اختبار t للعينة الواحدة.

الصورة التالية توضح الصيغ التي يمكننا استخدامها لحساب هذه القيم:

الخطوة 2: حساب إحصائية اختبار t .

بعد ذلك، سوف نقوم بحساب إحصائية اختبار t باستخدام الصيغة التالية:

ر = س – μ / (ق/ √ن )

ذهب:

س = متوسط العينة

μ = متوسط عدد السكان الافتراضي

s = عينة الانحراف المعياري

ن = حجم العينة

الصورة التالية توضح كيفية حساب t في Excel:

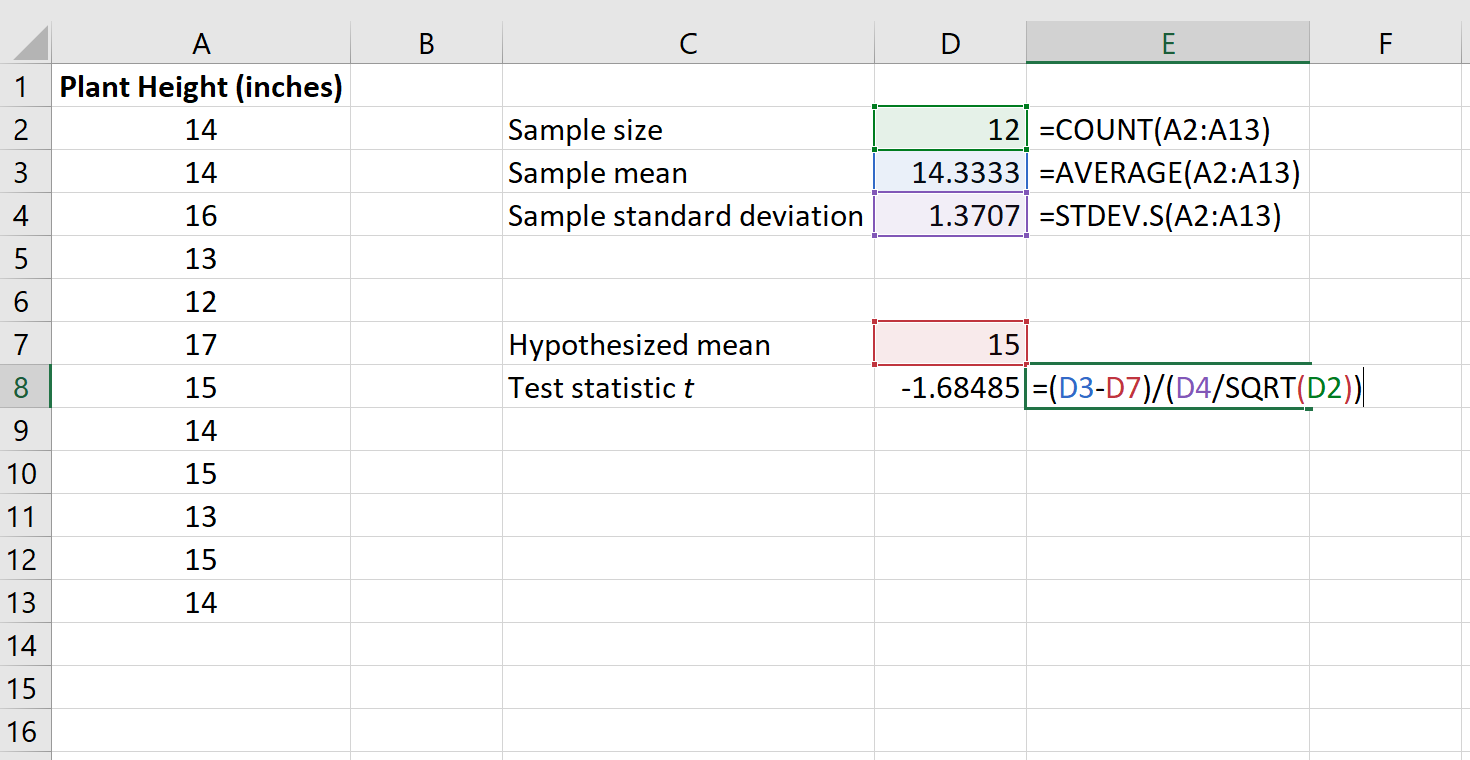
وتبين أن إحصائيات اختبار t هي -1.68485 .

الخطوة 3: احسب القيمة الاحتمالية لإحصائية الاختبار.

بعد ذلك، نحتاج إلى حساب القيمة p المرتبطة بإحصائيات الاختبار باستخدام الوظيفة التالية في Excel:

=T.DIST.2T(ABS(x)، درجة الحرية)

ذهب:

س = ر إحصائية الاختبار

deg_freedom = درجات الحرية للاختبار، وتحسب بـ n-1

الملاحظات الفنية:

ترجع الدالة T.DIST.2T() القيمة p لاختبار t ثنائي الطرف. إذا كنت تقوم بدلاً من ذلك بإجراء اختبار t لليسار أو لليمين، فيمكنك بدلاً من ذلك استخدام الدالتين T.DIST() أو T.DIST.RT() ، على التوالي.

توضح الصورة التالية كيفية حساب القيمة الاحتمالية لإحصائيات الاختبار الخاصة بنا:

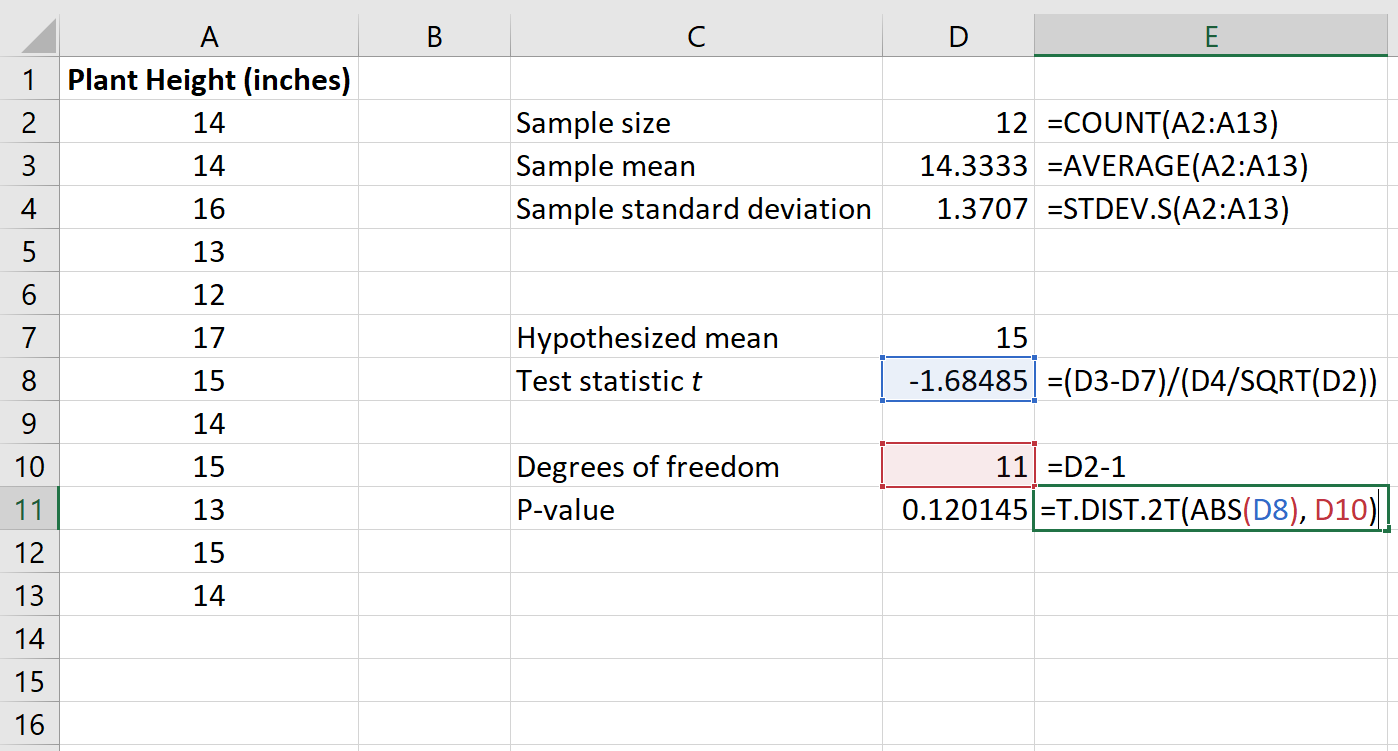
وتبين أن القيمة p هي 0.120145 .

الخطوة 4: تفسير النتائج.

الفرضيتين لهذا الاختبار t على عينة معينة هي كما يلي:

H ₀ : μ = 15 (متوسط ارتفاع هذا النوع من النباتات هو 15 بوصة)

H _A : μ ≠15 (متوسط الارتفاع ليس 15 بوصة)

نظرًا لأن القيمة p للاختبار (0.120145) أكبر من alpha = 0.05، فإننا نفشل في رفض الفرضية الصفرية للاختبار.

ليس لدينا أدلة كافية لنقول أن متوسط ارتفاع هذا النوع بالذات من النباتات هو أكثر من 15 بوصة.

مصادر إضافية

تشرح البرامج التعليمية التالية كيفية إجراء أنواع شائعة أخرى من اختبارات t في Excel:

كيفية إجراء اختبار t من عينتين في برنامج Excel
كيفية إجراء اختبار t للعينات المقترنة في Excel