المتوسط والوسيط والمنوال

تشرح هذه المقالة معنى المتوسط والوسيط والمنوال. ستتعلم كيفية الحصول على المتوسط والوسيط والمنوال، وما يتم استخدامه من أجله، وما هو الفرق بين هذه المقاييس الإحصائية الثلاثة. بالإضافة إلى ذلك، سوف تكون قادرًا على حساب المتوسط والوسيط والمنوال لأي عينة إحصائية باستخدام الآلة الحاسبة عبر الإنترنت في النهاية.

ما هو المتوسط والوسيط والمنوال؟

المتوسط والوسيط والوضع عبارة عن مقاييس إحصائية للموقع المركزي. بمعنى آخر، المتوسط والوسيط والمنوال هي قيم تساعد في تعريف العينة الإحصائية، فهي تشير بشكل خاص إلى ماهية قيمها المركزية.

يتم تعريف المتوسط والوسيط والوضع على النحو التالي:

• المتوسط : هو متوسط جميع البيانات في العينة.
• الوسيط : هذه هي القيمة الوسطى لجميع البيانات مرتبة من الأصغر إلى الأكبر.
• الوضع : هذه هي القيمة الأكثر تكرارًا في مجموعة البيانات.

يتم شرح هذه المقاييس الإحصائية الثلاثة بمزيد من التفصيل أدناه.

نصف

لحساب المتوسط، قم بجمع جميع القيم ثم قسمتها على إجمالي عدد البيانات. وبالتالي فإن صيغة المتوسط هي كما يلي:

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب المتوسط والوسيط والوضع لأي مجموعة بيانات.

الرمز المتوسط هو شريط أفقي فوق الحرف x

يمكنك أيضًا التمييز بين متوسط العينة ومتوسط المجتمع باستخدام رمز المتوسط: حيث يتم التعبير عن متوسط العينة باستخدام الرمز

، في حين أن متوسط عدد السكان يستخدم الحرف اليوناني

يُعرف المتوسط أيضًا بالوسط الحسابي أو المتوسط . علاوة على ذلك، فإن متوسط التوزيع الإحصائي يعادل توقعه الرياضي.

متوسط المثال

• حصل الطالب على الدرجات التالية خلال عام دراسي: في الرياضيات 9، في اللغة 7، في التاريخ 6، في الاقتصاد 8، وفي العلوم 7.5. ما هو متوسط جميع درجاتك؟

لإيجاد المتوسط الحسابي، نحتاج إلى جمع جميع الدرجات ثم قسمتها على إجمالي عدد المواد في المقرر، وهو 5. لذلك، نطبق صيغة المتوسط الحسابي:

نستبدل البيانات في الصيغة ونحسب الوسط الحسابي:

كما ترون، في المتوسط الحسابي، يتم تعيين نفس الوزن لكل قيمة، أي أن كل جزء من البيانات له نفس الوزن داخل الكل.

الوسيط

الوسيط هو القيمة الوسطى لجميع البيانات مرتبة من الأصغر إلى الأكبر. بمعنى آخر، يقوم الوسيط بتقسيم مجموعة البيانات المرتبة إلى جزأين متساويين.

يعتمد حساب الوسيط على ما إذا كان العدد الإجمالي للبيانات زوجيًا أم فرديًا:

• إذا كان العدد الإجمالي للبيانات فرديًا ، فسيكون الوسيط هو القيمة التي تقع في منتصف البيانات. وهذا يعني القيمة الموجودة في الموضع (n+1)/2 من البيانات المصنفة.



• إذا كان العدد الإجمالي لنقاط البيانات زوجيًا ، فسيكون الوسيط هو متوسط نقطتي البيانات الموجودتين في المركز. وهذا يعني المتوسط الحسابي للقيم الموجودة في الموضعين n/2 وn/2+1 من البيانات المطلوبة.

ذهب

هو العدد الإجمالي لعناصر البيانات في العينة.

غالبًا ما يستخدم المصطلح Me كرمز للإشارة إلى أن القيمة هي الوسيط لجميع الملاحظات.

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب المتوسط والوسيط والوضع لأي مجموعة بيانات.

مثال متوسط

• أوجد الوسيط للبيانات التالية: 3، 4، 1، 6، 7، 4، 8، 2، 8، 4، 5

أول شيء يجب فعله قبل إجراء العمليات الحسابية هو تصنيف البيانات، أي وضع الأرقام من الأصغر إلى الأكبر.

في هذه الحالة لدينا 11 ملاحظة، وبالتالي فإن العدد الإجمالي للبيانات فردي. ولذلك، فإننا نطبق الصيغة التالية لحساب موضع الوسيط:

وبالتالي سيكون الوسيط هو البيانات الموجودة في المركز السادس، والتي تتوافق في هذه الحالة مع القيمة 4.

موضة

في الإحصائيات، الوضع هو القيمة الموجودة في مجموعة البيانات التي لها أعلى تكرار مطلق، أي أن الوضع هو القيمة الأكثر تكرارًا في مجموعة البيانات.

لذلك، لحساب وضع مجموعة البيانات الإحصائية، ما عليك سوى حساب عدد المرات التي يظهر فيها كل عنصر بيانات في العينة، وستكون البيانات الأكثر تكرارًا هي الوضع.

يمكن أيضًا القول أن الوضع هو الوضع الإحصائي أو القيمة المشروطة . وبالمثل، عندما يتم تجميع البيانات في فواصل زمنية، فإن الفاصل الزمني الأكثر تكرارًا هو الفاصل المشروط أو الفئة المشروطة .

بشكل عام، يتم استخدام المصطلح Mo كرمز للوضع الإحصائي، على سبيل المثال، وضع التوزيع X هو Mo(X).

يمكن تمييز ثلاثة أنواع من الأوضاع حسب عدد القيم الأكثر تكرارًا:

• الوضع الأحادي : هناك قيمة واحدة فقط مع الحد الأقصى لعدد التكرارات. على سبيل المثال، [1، 4، 2، 4، 5، 3].
• الوضع ثنائي الوضع : الحد الأقصى لعدد التكرارات يحدث عند قيمتين مختلفتين، ويتم تكرار كلا القيمتين بنفس عدد المرات. على سبيل المثال، [2، 6، 7، 2، 3، 6، 9].
• الوضع المتعدد الوسائط : ثلاث قيم أو أكثر لها نفس الحد الأقصى لعدد التكرارات. على سبيل المثال، [3، 3، 4، 1، 3، 4، 2، 1، 4، 5، 2، 1].

👉 يمكنك استخدام الآلة الحاسبة أدناه لحساب المتوسط والوسيط والوضع لأي مجموعة بيانات.

مثال الموضة

• ما هو وضع مجموعة البيانات التالية؟

الأرقام غير مرتبة، لذا فإن أول شيء سنفعله هو فرزها. هذه الخطوة ليست إلزامية، لكنها ستساعدك في العثور على الموضة بسهولة أكبر.

الرقمان 2 و 9 يظهران مرتين، لكن الرقم 5 يتكرر ثلاث مرات. ولذلك، فإن وضع سلسلة البيانات هو رقم 5.

حل تمرين المتوسط والوسيط والمنوال

الآن بعد أن عرفت ما هو المتوسط والوسيط والمنوال، يوجد أدناه تمرين مفصل حول هذه المقاييس الإحصائية حتى تتمكن من رؤية كيفية حسابها بالضبط.

• أوجد المتوسط والوسيط والمنوال لمجموعة البيانات الإحصائية التالية:

للعثور على متوسط البيانات، علينا جمعها كلها، ثم قسمتها على إجمالي عدد البيانات، وهو 30:

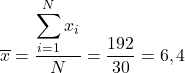
ثانيا، دعونا معرفة متوسط العينة. لذلك نقوم بترتيب جميع الأرقام تصاعديا:

في هذه الحالة، يكون العدد الإجمالي للبيانات زوجيًا، لذلك من الضروري حساب الموضعين المركزيين اللذين سيتم العثور على الوسيط بينهما. لهذا نستخدم الصيغتين التاليتين:

وبالتالي فإن الوسيط سيكون بين الموضع الخامس عشر والسادس عشر، وهو ما يتوافق على التوالي مع القيمتين 6 و 7. وبشكل أكثر دقة، فإن الوسيط يعادل متوسط هذه القيم:

وأخيرا، للعثور على الوضع، عليك فقط حساب جميع المرات التي يظهر فيها كل رقم. كما ترون، الرقم 6 والرقم 8 يظهران أربع مرات إجمالاً، وهو الحد الأقصى لعدد التكرارات. ولذلك، فهو في هذه الحالة وضع ثنائي والرقمين هما وضع مجموعة البيانات:

المتوسط الحسابي والوسيط والمنوال

أدخل البيانات من أي عينة إحصائية في الآلة الحاسبة الإلكترونية التالية لحساب متوسطها ووسيطها ومنوالها. يجب فصل البيانات بمسافة وإدخالها باستخدام النقطة كفاصل عشري.