مقاييس النزعة المركزية: التعريف والأمثلة
مقياس الاتجاه المركزي هو قيمة واحدة تمثل النقطة المركزية لمجموعة البيانات. يمكن أيضًا تسمية هذه القيمة باسم “الموقع المركزي” لمجموعة البيانات.
في الإحصاء، هناك ثلاثة مقاييس شائعة للاتجاه المركزي:
- المتوسط
- المتوسط
- الموضة
يقوم كل من هذه المقاييس بالعثور على الموقع المركزي لمجموعة البيانات باستخدام طرق مختلفة. اعتمادًا على نوع البيانات التي تقوم بتحليلها، قد يكون من الأفضل استخدام أحد هذه المقاييس الثلاثة بدلاً من المقاييس الأخرى.
في هذه المقالة، سنلقي نظرة على كيفية حساب كل من مقاييس النزعة المركزية الثلاثة بالإضافة إلى كيفية تحديد المقياس الأفضل للاستخدام بناءً على بياناتك.
لماذا تعتبر مقاييس الاتجاه المركزي مفيدة؟
قبل أن ننظر إلى كيفية حساب المتوسط والوسيط والمنوال، من المفيد أن نفهم سبب كون هذه القياسات مفيدة بالفعل في المقام الأول.
خذ بعين الاعتبار السيناريو التالي:
يحاول زوجان شابان تحديد مكان شراء منزلهما الأول في مدينة جديدة، وأقصى ما يمكنهما إنفاقه هو 150 ألف دولار. بعض مناطق المدينة لديها منازل باهظة الثمن، وبعضها منازل رخيصة، وبعضها منازل متوسطة السعر. إنهم يريدون تضييق نطاق بحثهم بسهولة ليشمل أحياء محددة تناسب ميزانيتهم.
إذا نظر الزوجان إلى أسعار منازل الأسرة الواحدة في كل حي، فقد يجدان صعوبة في تحديد الأحياء التي تناسب ميزانيتهما، لأنهما قد يريان شيئًا كهذا:
أسعار المنازل في الحي أ : 140,000 دولار، 190,000 دولار، 265,000 دولار، 115,000 دولار، 270,000 دولار، 240,000 دولار، 250,000 دولار، 180,000 دولار، 160,000 دولار، 200,000 دولار، 240,000 دولار، 280,000 دولار،…
أسعار المنازل في الحي ب : 140,000 دولار، 290,000 دولار، 155,000 دولار، 165,000 دولار، 280,000 دولار، 220,000 دولار، 155,000 دولار، 185,000 دولار، 160,000 دولار، 200,000 دولار، 190,000 دولار، 140,000 دولار، 145.0 دولار 0 0,…
أسعار المنازل في الحي C : 140,000 دولار، 130,000 دولار، 165,000 دولار، 115,000 دولار، 170,000 دولار، 100,000 دولار، 150,000 دولار، 180,000 دولار، 190,000 دولار، 120,000 دولار، 110,000 دولار، 130,000 دولار، 120,0 دولار 0 0,…
ومع ذلك، إذا كانوا يعرفون متوسط السعر (على سبيل المثال، مقياس الاتجاه المركزي) للمنازل في كل حي، فيمكنهم تحسين بحثهم بسرعة أكبر لأنه يمكنهم بسهولة تحديد أي حي لديه أسعار منازل تتوافق مع ميزانيتهم:
متوسط سعر المنزل في الحي أ: 220 ألف دولار
متوسط سعر المنزل في الحي ب : 190.000 دولار
متوسط سعر المنزل في الحي C : 140.000 دولار
ومن خلال معرفة متوسط سعر المنزل في كل حي، يمكنهم أن يروا بسرعة أن الحي ” ج” من المرجح أن يكون لديه أكبر عدد من المنازل المتاحة في حدود ميزانيتهم.
هذه هي فائدة استخدام مقياس الاتجاه المركزي: فهو يساعدك على فهم القيمة المركزية لمجموعة البيانات، والتي تميل إلى وصف مكان وجود قيم البيانات بشكل عام. في هذا المثال بالذات، يساعد الزوجين الشابين على فهم السعر النموذجي للمنزل في كل حي.
الخلاصة: يعد قياس الاتجاه المركزي مفيدًا لأنه يزودنا بقيمة واحدة تصف “مركز” مجموعة البيانات. يساعدنا هذا على فهم مجموعة البيانات بشكل أسرع بكثير من مجرد النظر إلى جميع القيم الفردية في مجموعة البيانات.
يقصد
المقياس الأكثر استخدامًا للنزعة المركزية هو المتوسط . لحساب متوسط مجموعة بيانات، ما عليك سوى إضافة كل القيم الفردية وتقسيمها على إجمالي عدد القيم.
المتوسط = (مجموع كل القيم) / (إجمالي عدد القيم)
على سبيل المثال، لنفترض أن لدينا مجموعة البيانات التالية التي توضح عدد الضربات التي حققها 10 لاعبين بيسبول في نفس الفريق خلال موسم واحد على أرضهم:
| لاعب | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #عشرة |
|---|---|---|---|---|---|---|---|---|---|---|
| يدير المنزل | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
يمكن حساب متوسط عدد الضربات المنزلية لكل لاعب على النحو التالي:
المتوسط = (8+15+22+21+12+9+11+27+14+13) / 10 = 15.2 دائرة .
الوسيط
الوسيط هو القيمة الوسطى لمجموعة البيانات. يمكنك العثور على الوسيط عن طريق ترتيب جميع القيم الفردية في مجموعة البيانات من الأصغر إلى الأكبر وإيجاد القيمة المتوسطة. إذا كان هناك عدد فردي من القيم، فإن الوسيط هو القيمة الوسطى. إذا كان هناك عدد زوجي من القيم، فإن الوسيط هو متوسط القيمتين الأوسطتين.
على سبيل المثال، للعثور على متوسط عدد الضربات على أرضه التي حققها 10 من لاعبي البيسبول في المثال السابق، يمكننا ترتيب اللاعبين بترتيب تنازلي لعدد الضربات على أرضه:
| لاعب | #1 | #6 | #7 | #5 | #عشرة | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| يدير المنزل | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
وبما أن لدينا عددًا زوجيًا من القيم، فإن الوسيط هو ببساطة متوسط القيمتين الأوسطتين: 13.5 .
بدلًا من ذلك، فكر فيما إذا كان لدينا تسعة لاعبين:
| لاعب | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| يدير المنزل | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
في هذه الحالة، نظرًا لأن لدينا عددًا فرديًا من القيم، فإن الوسيط هو ببساطة القيمة الوسطى: 14 .
الموضة
الوضع هو القيمة التي تظهر غالبًا في مجموعة البيانات. يمكن أن لا تحتوي مجموعة البيانات على أوضاع (في حالة عدم تكرار القيم)، أو وضع واحد، أو أوضاع متعددة.
على سبيل المثال، مجموعة البيانات التالية لا تحتوي على وضع:
| لاعب | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #عشرة |
|---|---|---|---|---|---|---|---|---|---|---|
| يدير المنزل | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
تحتوي مجموعة البيانات التالية على الوضع: 15 . هذه هي القيمة التي تظهر بشكل متكرر.
| لاعب | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #عشرة |
|---|---|---|---|---|---|---|---|---|---|---|
| يدير المنزل | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
تحتوي مجموعة البيانات التالية على ثلاثة أوضاع: 8، 15، 19 . هذه هي القيم التي تظهر في أغلب الأحيان.
| لاعب | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #عشرة |
|---|---|---|---|---|---|---|---|---|---|---|
| يدير المنزل | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
يمكن أن يكون الوضع مقياسًا مفيدًا بشكل خاص للاتجاه المركزي عند التعامل مع البيانات الفئوية، لأنه يخبرنا بالفئة التي تظهر بشكل متكرر. على سبيل المثال، ضع في اعتبارك المخطط الشريطي التالي الذي يعرض نتائج استطلاع حول اللون المفضل للأشخاص:
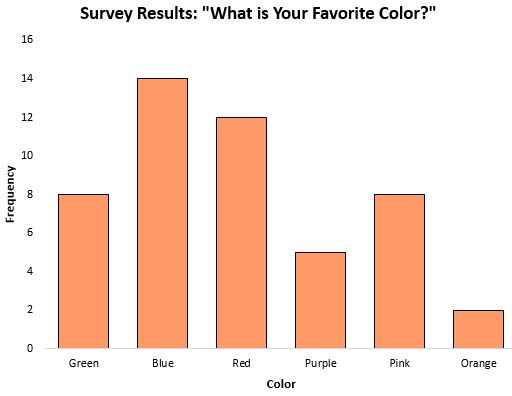
كان الوضع ، أو الاستجابة التي حدثت بشكل متكرر، باللون الأزرق.
في السيناريوهات التي تكون فيها البيانات فئوية (مثل تلك المذكورة أعلاه)، ليس من الممكن حتى حساب الوسيط أو المتوسط، وبالتالي فإن الوضع هو المقياس الوحيد للاتجاه المركزي الذي يمكننا استخدامه.
يمكن أيضًا استخدام الوضع للبيانات الرقمية، كما رأينا في المثال أعلاه مع لاعبي البيسبول. ومع ذلك، يميل الوضع إلى أن يكون أقل فائدة للإجابة على السؤال “ما هي القيمة النموذجية لمجموعة البيانات هذه؟” »
على سبيل المثال، لنفترض أننا نريد معرفة العدد النموذجي للركلات التي يضربها لاعب بيسبول في هذا الفريق:
| لاعب | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #عشرة |
|---|---|---|---|---|---|---|---|---|---|---|
| يدير المنزل | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
وضع مجموعة البيانات هذه هو 8 و15 و19 لأن هذه هي القيم الأكثر شيوعًا. ومع ذلك، فهذه ليست مفيدة جدًا في فهم العدد النموذجي من الضربات على أرض الملعب التي يقوم بها لاعب في الفريق. والمقياس الأفضل للاتجاه المركزي في هذه الحالة هو الوسيط (15) أو المتوسط (15 أيضًا).
يعد الوضع أيضًا مقياسًا ضعيفًا للاتجاه المركزي عندما يكون رقمًا بعيدًا عن بقية القيم. على سبيل المثال، وضع مجموعة البيانات التالية هو 30، لكن هذا لا يمثل في الواقع العدد “النموذجي” لعدد مرات الجري على أرضه لكل لاعب في الفريق:
| لاعب | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #عشرة |
|---|---|---|---|---|---|---|---|---|---|---|
| يدير المنزل | 5 | 6 | 7 | عشرة | 11 | 12 | 13 | 15 | 30 | 30 |
مرة أخرى، المتوسط أو الوسيط يقوم بعمل أفضل في وصف الموقع المركزي لمجموعة البيانات هذه.
متى يتم استخدام المتوسط والوسيط والوضع
لقد رأينا أن المتوسط والوسيط والمنوال جميعهم يقيسون الموقع المركزي، أو “القيمة النموذجية”، لمجموعة البيانات بطرق مختلفة جدًا:
المتوسط: يبحث عن القيمة المتوسطة في مجموعة بيانات.
الوسيط: يبحث عن القيمة المتوسطة في مجموعة بيانات.
الوضع: يبحث عن القيمة الأكثر تكرارًا في مجموعة البيانات.
فيما يلي بعض السيناريوهات التي يكون فيها استخدام بعض مقاييس النزعة المركزية أفضل من غيرها:
متى يستخدم المتوسط
من الأفضل استخدام المتوسط عندما يكون توزيع البيانات متماثلًا إلى حد ما ولا توجد قيم متطرفة.
على سبيل المثال، لنفترض أن لدينا التوزيع التالي الذي يوضح رواتب الأفراد في مدينة معينة:
وبما أن هذا التوزيع متماثل إلى حد ما (أي إذا قمت بتقسيمه إلى نصفين، فسيبدو كل نصف متساويًا تقريبًا) ولا توجد قيم متطرفة (على سبيل المثال (على سبيل المثال، لا توجد رواتب مرتفعة للغاية)، فإن المتوسط سيقوم بعمل جيد في وصف مجموعة البيانات هذه.
وتبين أن المتوسط يبلغ 63000 دولار، وهو تقريبًا في وسط التوزيع:
متى يتم استخدام الوسيط
من الأفضل استخدام الوسيط عندما يكون توزيع البيانات منحرفًا أو عندما تكون هناك قيم متطرفة.
البيانات المتحيزة:
عندما يكون التوزيع منحرفًا، يظل الوسيط قادرًا على التقاط الموقع المركزي. على سبيل المثال، خذ بعين الاعتبار التوزيع التالي لرواتب الأفراد في مدينة معينة:
ويعكس المتوسط الراتب “النموذجي” للفرد بشكل أفضل من المتوسط. وذلك لأن القيم الكبيرة عند ذيل التوزيع تميل إلى تحريك المتوسط بعيدًا عن المركز وباتجاه الذيل الطويل.
في هذا المثال بالذات، يخبرنا المتوسط أن الفرد العادي يكسب حوالي 47000 دولار سنويًا في هذه المدينة، بينما يخبرنا المتوسط أن الفرد النموذجي يكسب حوالي 32000 دولار سنويًا فقط، وهو ما يمثل أكثر تمثيلًا للفرد النموذجي.
القيم المتطرفة:
ويساعد الوسيط أيضًا على التقاط الموقع المركزي للتوزيع بشكل أفضل عندما تكون هناك قيم متطرفة في البيانات. على سبيل المثال، خذ بعين الاعتبار الرسم البياني التالي الذي يوضح المساحة المربعة للمنازل في شارع معين:
ويتأثر المتوسط بشدة بعدد قليل من المنازل الكبيرة للغاية، في حين أن المتوسط لا يتأثر. وبالتالي، يقوم الوسيط بعمل أفضل في التقاط اللقطات المربعة “النموذجية” لمنزل في ذلك الشارع من المتوسط.
متى تستخدم الوضع
يُفضل استخدام هذا الوضع عندما تعمل مع البيانات الفئوية وتريد معرفة الفئة التي تظهر بشكل متكرر. وهنا بعض الأمثلة:
- أنت تجري استطلاعًا حول الألوان المفضلة للأشخاص وتريد معرفة اللون الذي يظهر بشكل متكرر في الردود.
- أنت تجري استطلاعًا لتفضيلات الأشخاص من بين ثلاثة خيارات لتصميم موقع الويب وتريد معرفة التصميم الذي يفضله الأشخاص أكثر.
كما ذكرنا سابقًا، إذا كنت تتعامل مع بيانات فئوية، فليس من الممكن حتى حساب الوسيط أو المتوسط، مما يترك الوضع باعتباره المقياس الوحيد للاتجاه المركزي.
بشكل عام، إذا كنت تتعامل مع بيانات رقمية مثل اللقطات المربعة للمنازل، وعدد مرات ضرب المنازل لكل لاعب، والراتب لكل فرد، وما إلى ذلك، فمن الأفضل عادةً استخدام الوسيط أو المتوسط لوصف القيمة “النموذجية” في مجموعة البيانات.
ملاحظة: من المهم ملاحظة أنه إذا تم توزيع مجموعة البيانات بشكل طبيعي تمامًا ، فإن المتوسط والوسيط والمنوال جميعهم لهم نفس القيمة.
About Author
دكتور بنيامين أندرسون
مرحبًا، أنا بنجامين، أستاذ الإحصاء المتقاعد الذي تحول إلى مدرس متخصص في Statorials. بفضل خبرتي الواسعة في مجال الإحصاء، فأنا حريص على مشاركة معرفتي لتمكين الطلاب من خلال Statorials. تعرف أكثر