为什么中位数在统计学中很重要？

中位数表示数据集的中间值，所有值均按从小到大排序。

例如，以下数据集中的中位数为 19：

数据集：3、4、11、15、19、22、23、23、26

中位数还代表数据集的^{第 50 个}百分位。也就是说，数据集中正好有一半的值高于中位数，一半的值低于中位数。

中位数是一个重要的计算指标，因为它让我们了解数据集的“中心”在哪里。这也让我们了解给定数据集中的“典型”值。

例如，假设我们有一个数据集，其中包含某个城市 10,000 套不同房屋的销售价格。

我们可以计算中值来快速了解该城市房屋的平均销售价格，而不是查看一行又一行的原始数据。

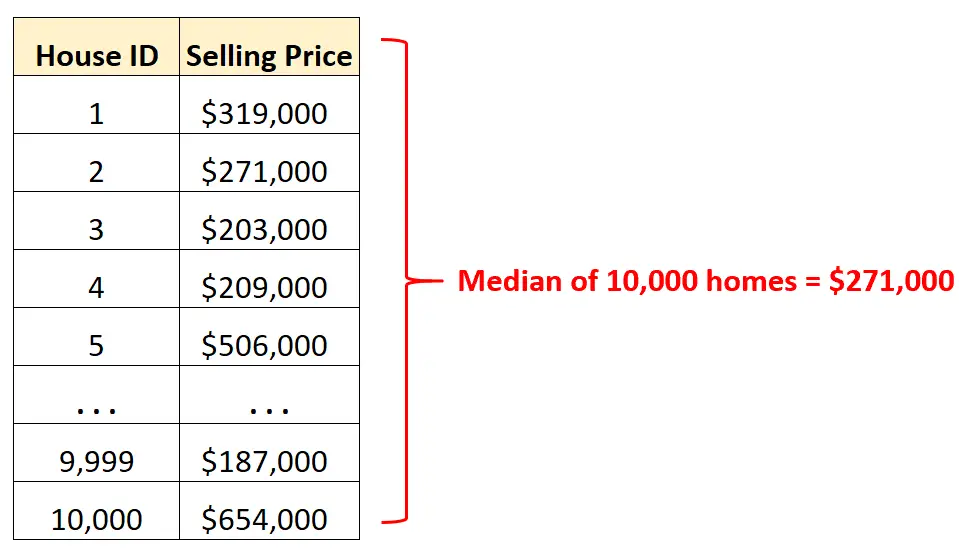
知道销售价格中位数为 271,000 美元后，我们知道 10,000 套房屋中有一半的售价高于该价格，而另一半的售价则低于该价格。

这也让我们了解了这座城市房屋的“典型”销售价格。

何时使用中位数

在分析数据集时，我们常常想了解中心价值在哪里。

在统计学中，我们使用两个常见的指标来衡量数据集的中心：

• 平均值：一组数据的平均值
• 中位数：数据集中的中值

事实证明，在以下情况下中位数是更有用的衡量标准：

• 当分布不对称时。
• 当分布包含异常值时。

为了说明这一点，请考虑以下两个示例。

示例 1：计算偏态分布的中位数

考虑某个城市居民的工资分布如下：

中位数比平均值更能反映居民的“典型”工资，因为分布向右倾斜。

这意味着分布右侧的高工资将平均值推离分布的中心。

在此特定示例中，平均工资为 47,000 美元，而中位数工资为 32,000 美元。中位数更能代表这个城市的典型工资。

示例 2：计算存在异常值的情况下的中位数

考虑下图，它显示了某条街道上房屋的平方英尺：

平均值很大程度上受到一些非常大的房屋的影响，而中位数则不然。

我们可以看到，中位数比平均值更能捕捉该街道上房屋的“典型”平方英尺，因为它不受异常值的影响。

概括

以下是本文要点的简要总结：

• 中位数表示数据集中的中间值。
• 中位数很重要，因为它让我们了解数据集中的中心值在哪里。
• 当分布倾斜和/或存在异常值时，中位数往往比平均值更有用。

其他资源

具体示例：使用平均值、中位数和众数
何时使用平均值与平均值中位数：带有示例
为什么众数在统计学中很重要？