中等差异
本文解释了什么是平均偏差及其计算方法。您还将找到计算平均偏差的具体示例。此外,您将能够使用在线计算器计算任何统计数据集的平均偏差。
什么是平均偏差?
平均偏差,也称为平均绝对偏差,是统计离散度的度量。
数据集的平均偏差是绝对偏差的平均值。因此,平均偏差等于每个数据项与算术平均值的偏差之和除以数据项总数。
换句话说,平均偏差的公式如下:

👉您可以使用下面的计算器来计算任何数据集的平均偏差。
在统计学中,平均偏差也称为平均绝对偏差。
平均偏差的解释如下:平均偏差的值越大,这意味着数据平均离算术平均值越远;反之,平均偏差越低,值越接近。数据是。因此,平均偏差表明数据系列的离散程度。
其他被视为分布的度量有极差、四分位距、标准差(或标准差)、方差和变异系数。
如何计算平均偏差
要计算数据系列的平均偏差,必须遵循以下步骤:
- 计算统计数据集的算术平均值。
- 计算每个数据点与均值的偏差,定义为数据与均值之差的绝对值。
- 将上一步中计算出的所有差异相加。
- 除以数据总数。得到的结果就是数据系列的平均偏差。
总之,计算平均偏差必须使用的公式为:
![]()
计算平均偏差的示例
考虑到平均偏差的定义,下面是计算统计样本平均偏差的分步解决示例。这样您将更好地了解如何获得平均偏差。
- 分析师研究一家公司过去一年的经济业绩,并了解该公司在该年每个季度获得的利润信息:2、3、7 和 500 万美元。数据的平均偏差是多少?
首先,我们需要对数据进行平均,因此我们将求和除以观测总数 (4):
![]()
计算出算术平均值后,我们使用均值偏差公式:
![]()
我们将数据代入公式:
![]()
我们用分子进行计算:
![]()
![]()
![]()
最后除以数据总数即可得到样本的平均偏差:
![]()
平均偏差计算器
将一组统计数据输入下面的计算器中,计算其平均偏差。数据必须用空格分隔,并使用句点作为小数点分隔符输入。
分组数据的平均偏差
要计算按区间分组的数据的平均偏差,必须遵循以下步骤:
- 确定统计数据集的算术平均值。由于数据是分组的,计算平均值的表达式为:
- 计算每个区间与均值的偏差,相当于班级成绩与均值之差的绝对值。
- 将每个间隔的偏差乘以其绝对频率。
- 将上一步的所有结果相加,然后除以数据总数。获得的结果是按区间分组的样本的平均偏差。
![]()
![]()
![]()
![]()
综上所述,获得分组数据平均偏差的公式为:
![]()
当数据被分组时,通常意味着有很多数据,并且找到平均偏差需要很多步骤。因此,通常使用频数表来进行计算。
以下是有关如何计算数据分组为区间时的平均偏差的分步练习:
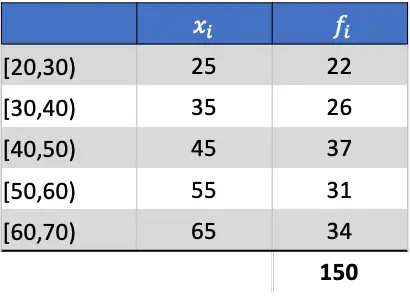
首先要做的是计算分组数据的平均值。为此,我们通过将课堂笔记乘以其频率来向表中添加一列:
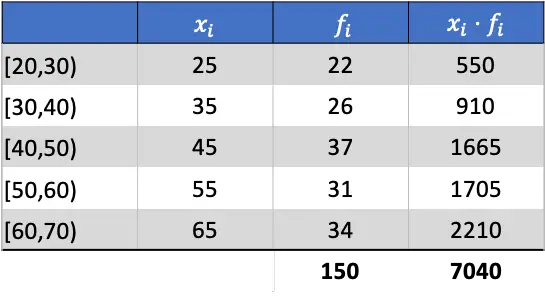
因此,算术平均值将是添加列的总和除以绝对频率总和的结果:
![]()
现在我们知道了数据的平均值,我们可以添加所有必要的列来找到平均偏差:
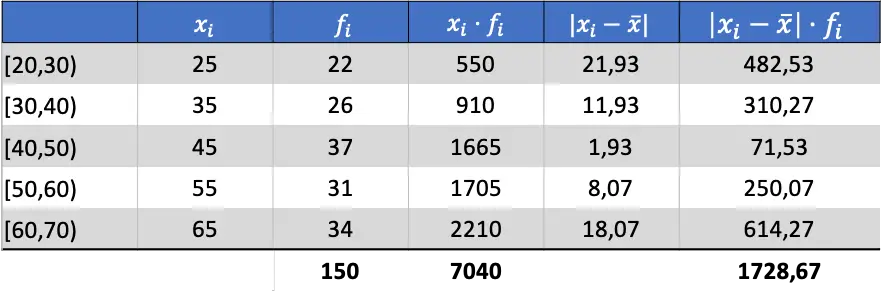
因此,要获得平均偏差,您必须将最后一列的总和除以观测值总数:
![]()