如何在 r 中执行二次回归
当两个变量存在线性关系时,我们通常可以使用简单线性回归来量化它们的关系。

然而,当两个变量存在二次关系时,我们可以使用二次回归来量化它们的关系。

本教程介绍如何在 R 中执行二次回归。
示例:R 中的二次回归
假设我们想了解工作时间与幸福感之间的关系。我们有以下关于 11 名不同的人每周工作时数和报告的幸福程度(范围为 0 到 100)的数据:

使用以下步骤在 R 中拟合二次回归模型。
第 1 步:输入数据。
首先,我们将创建一个包含数据的数据框:
#createdata data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60), happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27)) #viewdata data hours happiness 1 6 14 2 9 28 3 12 50 4 14 70 5 30 89 6 35 94 7 40 90 8 47 75 9 51 59 10 55 44 11 60 27
第 2 步:可视化数据。
接下来,我们将创建一个简单的散点图来可视化数据。
#create scatterplot
plot(data$hours, data$happiness, pch=16)
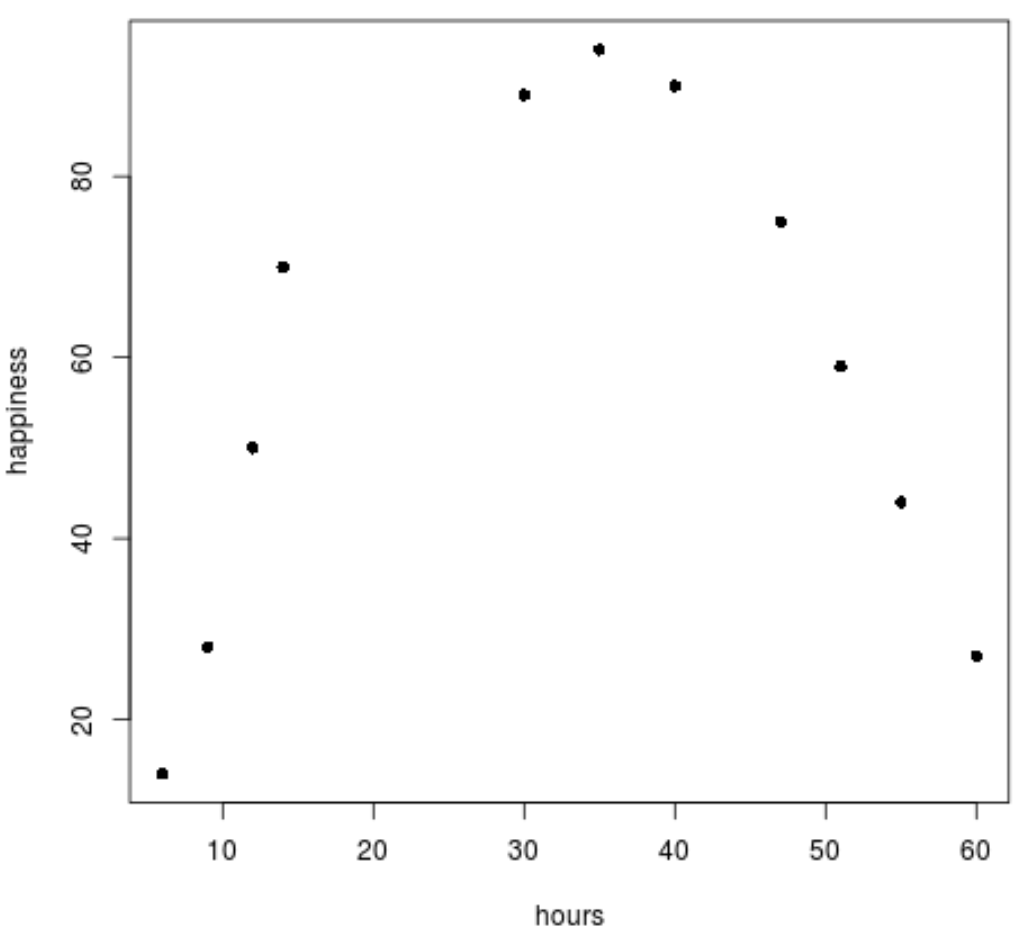
我们可以清楚地看到数据不遵循线性模式。
步骤 3:拟合一个简单的线性回归模型。
接下来,我们将拟合一个简单的线性回归模型,看看它与数据的拟合程度如何:
#fit linear model linearModel <- lm(happiness ~ hours, data=data) #view model summary summary(linearModel) Call: lm(formula = happiness ~ hours) Residuals: Min 1Q Median 3Q Max -39.34 -21.99 -2.03 23.50 35.11 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 48.4531 17.3288 2.796 0.0208 * hours 0.2981 0.4599 0.648 0.5331 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 28.72 on 9 degrees of freedom Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331
如多重 R 平方值所示,模型解释的幸福感总方差仅为4.46% 。
步骤 4:拟合二次回归模型。
接下来,我们将拟合二次回归模型。
#create a new variable for hours 2 data$hours2 <- data$hours^2 #fit quadratic regression model quadraticModel <- lm(happiness ~ hours + hours2, data=data) #view model summary summary(quadraticModel) Call: lm(formula = happiness ~ hours + hours2, data = data) Residuals: Min 1Q Median 3Q Max -6.2484 -3.7429 -0.1812 1.1464 13.6678 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -18.25364 6.18507 -2.951 0.0184 * hours 6.74436 0.48551 13.891 6.98e-07 *** hours2 -0.10120 0.00746 -13.565 8.38e-07 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 6.218 on 8 degrees of freedom Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06
模型解释的幸福感总方差增加至96.02% 。
我们可以使用以下代码来可视化模型与数据的拟合程度:
#create sequence of hour values hourValues <- seq(0, 60, 0.1) #create list of predicted happiness levels using quadratic model happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2)) #create scatterplot of original data values plot(data$hours, data$happiness, pch=16) #add predicted lines based on quadratic regression model lines(hourValues, happinessPredict, col='blue')
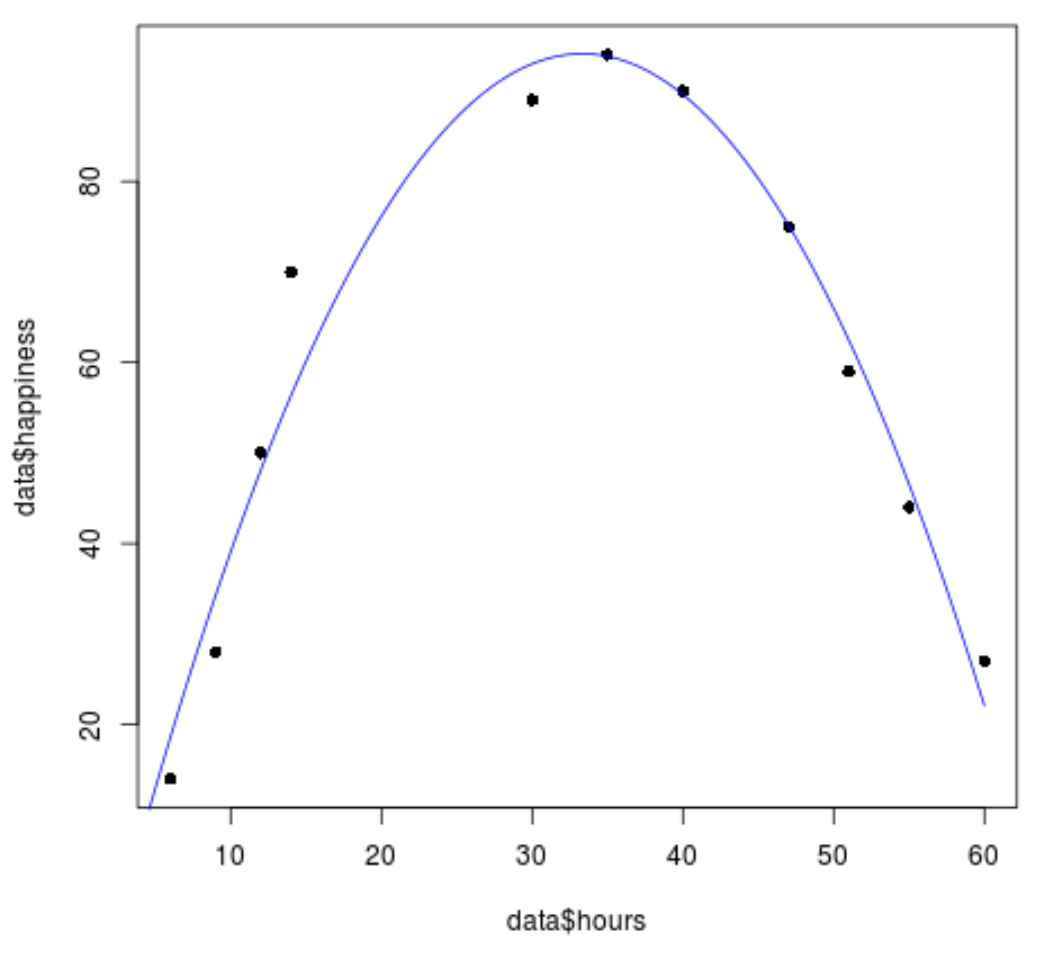
我们可以看到二次回归线与数据值拟合得相当好。
步骤 5:解释二次回归模型。
在上一步中,我们看到二次回归模型的结果是:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -18.25364 6.18507 -2.951 0.0184 *
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
根据此处提供的系数,调整后的二次回归将是:
幸福 = -0.1012(小时) 2 + 6.7444(小时)– 18.2536
我们可以使用这个方程来计算一个人在每周工作时数的情况下的预期幸福感。
例如,一个每周工作 60 小时的人的幸福指数为22.09 :
幸福 = -0.1012(60) 2 + 6.7444(60) – 18.2536 = 22.09
相反,每周工作 30 小时的人的幸福指数应该为92.99 :
幸福 = -0.1012(30) 2 + 6.7444(30) – 18.2536 = 92.99