二项分布简介
二项式分布是统计学中最流行的分布之一。要理解二项式分布,首先了解二项式实验会有所帮助。
二项式实验
二项式实验是具有以下属性的实验:
- 该实验由n次重复试验组成。
- 每个试验只有两种可能的结果。
- 每次试验的成功概率(表示为p )是相同的。
- 每个测试都是独立的。
二项式实验最明显的例子是抛硬币。例如,假设我们抛硬币 10 次。这是一个二项式实验,因为它具有以下四个属性:
- 该实验由n次重复试验组成——共有 10 次试验。
- 每次试验只有两种可能的结果:正面或反面。
- 每次试验的成功概率(表示为p )是相同的。如果我们将“成功”定义为着陆头,那么每次尝试的成功概率恰好为 0.5。
- 每次试验都是独立的——抛一枚硬币的结果不会影响任何其他抛硬币的结果。
二项式分布
二项式分布描述了在n次二项式实验中获得k次成功的概率。
如果随机变量X服从二项式分布,则X = k成功的概率可以通过以下公式求出:
P(X=k) = n C k * p k * (1-p) nk
金子:
- n:试验次数
- k:成功次数
- p:给定试验的成功概率
- n C k :在n次试验中获得k次成功的方法数
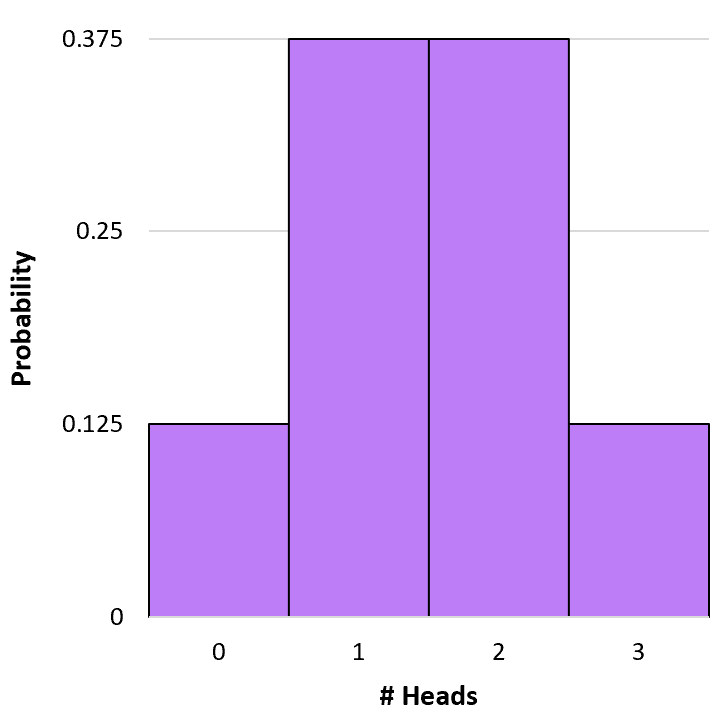
例如,假设我们抛硬币 3 次。我们可以使用上面的公式来确定这 3 次抛掷中获得 0、1、2 和 3 次正面朝上的概率:
P(X=0) = 3 C 0 * 0.5 0 * (1-0.5) 3-0 = 1 * 1 * (0.5) 3 = 0.125
P(X=1) = 3 C 1 * 0.5 1 * (1-0.5) 3-1 = 3 * 0.5 * (0.5) 2 = 0.375
P(X=2) = 3 C 2 * 0.5 2 * (1-0.5) 3-2 = 3 * 0.25 * (0.5) 1 = 0.375
P(X=3) = 3 C 3 * 0.5 3 * (1-0.5) 3-3 = 1 * 0.125 * (0.5) 0 = 0.125
注意:我们使用这个组合计算器来计算每个示例的nCk 。
我们可以创建一个简单的直方图来可视化此概率分布:
累积二项式概率的计算
使用上面的公式计算单个二项式概率(例如,硬币 3 次抛掷 1 次正面朝上的概率)很简单,但要计算累积二项式概率,我们需要添加各个概率。
例如,假设我们想知道一枚硬币在 3 次抛掷中出现 1 次或更少的正面朝上的概率。我们将使用以下公式来计算该概率:
P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 。
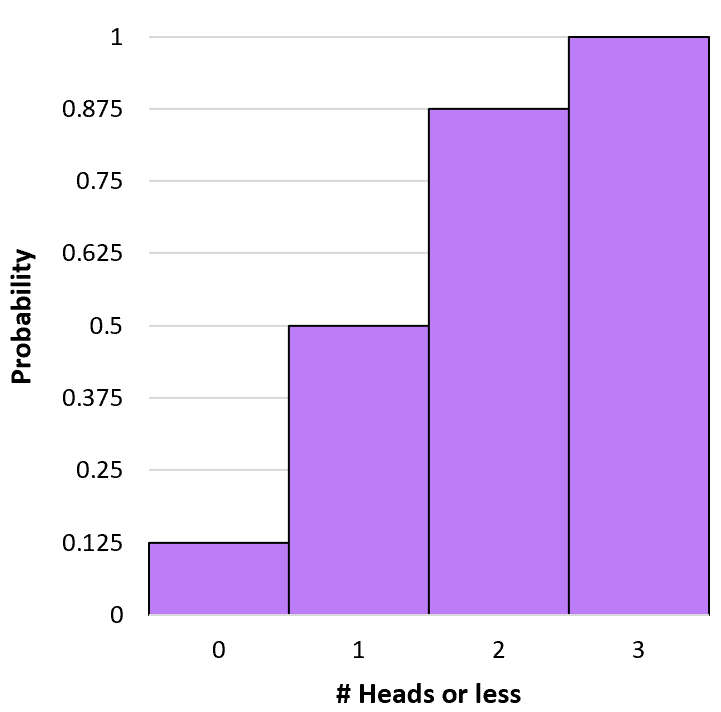
这称为累积概率,因为它涉及添加多个概率。我们可以使用类似的公式计算每个结果获得k 个或更少正面朝上的累积概率:
P(X≤0) = P(X=0) = 0.125 。
P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 。
P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0.125 + 0.375 + 0.375 = 0.875 。
P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0.125 + 0.375 + 0.375 + 0.125 = 1 。
我们可以创建一个直方图来可视化这个累积概率分布:
二项式概率计算器
当我们处理小数字时(例如 3 次硬币抛掷),手动计算二项式概率是合理的。然而,当我们处理较大的数字(例如 100 次抽奖)时,手动计算概率可能会很困难。在这些情况下,使用如下所示的二项式概率计算器会很有帮助。
例如,假设我们抛一枚硬币 n = 100 次,在给定的试验中,它落在正面的概率为 p = 0.5,我们想知道它落在正面的概率 k = 43 次或更少:
P(X= 43 ) = 0.03007
P(X< 43 ) = 0.06661
P( X≤43 )= 0.09667
P(X> 43 ) = 0.90333
P( X≥43 ) = 0.93339
以下是如何解释结果:
- 硬币出现 43 次正面的概率是0.03007 。
- 硬币正面朝上少于 43 次的概率是0.06661 。
- 硬币正面朝上 43 次或更少的概率为0.09667 。
- 硬币正面朝上超过 43 次的概率是0.90333 。
- 硬币正面朝上 43 次或以上的概率为0.93339 。
二项分布的性质
二项式分布具有以下性质:
分布的平均值为μ = np
分布的方差为σ 2 = np(1-p)
分布的标准差为σ = √ np(1-p)
例如,假设我们抛一枚硬币 3 次。设 p = 硬币正面朝上的概率。
我们期望的平均头数是 μ = np = 3*.5 = 1.5 。
我们期望的人数方差为 σ 2 = np(1-p) = 3*.5*(1-.5) = 0.75 。
二项式分布练习题
使用以下练习题来测试您对二项式分布的了解。
问题1
问题:鲍勃的罚球命中率为 60%。如果他罚球 12 次,他罚中 10 次的概率是多少?
答案:使用上面的二项式分布计算器,其中 p = 0.6、n = 12 和 k = 10,我们发现 P(X=10) = 0.06385 。
问题2
问题:杰西卡抛硬币 5 次。硬币正面朝上两次或更少的概率是多少?
答案:使用上面的二项式分布计算器,p = 0.5、n = 5 和 k = 2,我们发现 P(X≤2) = 0.5 。
问题3
问题:某个学生被某所大学录取的概率是 0.2。如果有 10 名学生申请,超过 4 名学生被录取的概率是多少?
答案:使用上面的二项式分布计算器,其中 p = 0.2、n = 10 且 k = 4,我们发现 P(X>4) = 0.03279 。
问题4
问题:抛硬币 12 次。预计出现的平均头像数是多少?
答案:回想一下,二项式分布的均值计算公式为 μ = np。因此,μ = 12*0.5 = 6 个头。
问题5
问题:马克有 10% 的出手次数能打出全垒打。如果他在一场比赛中出击 5 次,他击中的本垒打数量的差异是多少?
答案:回想一下,二项式分布的方差计算公式为 σ 2 = np(1-p)。因此, σ2 = 6*.1*(1-.1) = 0.54 。
其他资源
以下文章可以帮助您学习如何在不同的统计软件中使用二项分布: