了解二项式分布的形状
二项式分布描述了在n次二项式实验中获得k次成功的概率。
如果随机变量X服从二项式分布,则X = k成功的概率可以通过以下公式求出:
P(X=k) = n C k * p k * (1-p) nk
金子:
- n:试验次数
- k:成功次数
- p:给定试验的成功概率
- n C k :在n次试验中获得k次成功的方法数
当出现以下两种情况中的一种或多种时,二项式概率分布趋于钟形:
1.样本量(n)大。
2.给定试验的成功概率 (p) 接近 0.5。
然而,当这些条件都不发生时,二项式概率分布往往会出现偏差。为了说明这一点,请考虑以下示例:
示例1:样本量(n)较大
下图显示了 n = 200且 p = 0.5时的概率分布。
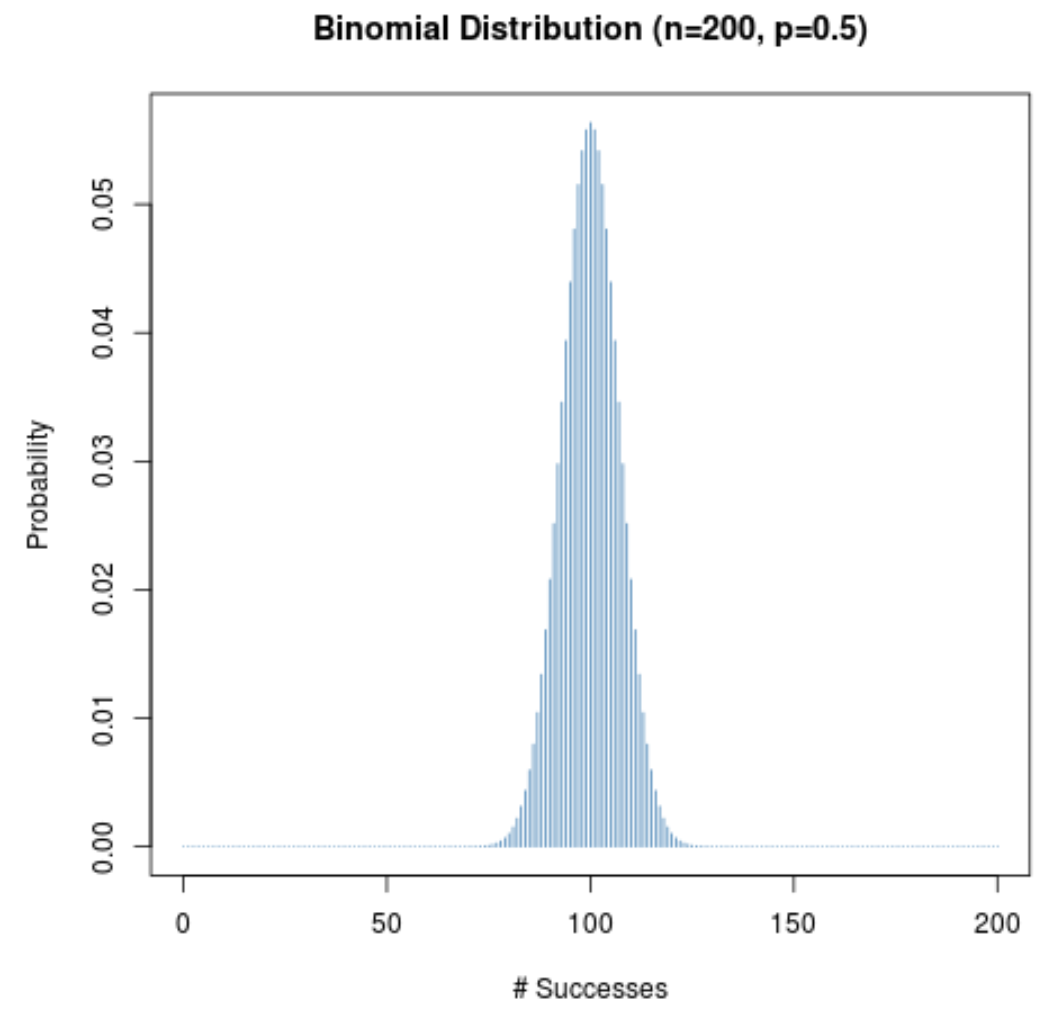
x 轴显示 200 次试验的成功次数,y 轴显示该成功次数发生的概率。
由于(1)样本量较大且(2)给定试验的成功概率接近 0.5,因此概率分布呈钟形。
即使给定试验的成功概率 (p) 不接近 0.5,只要样本量 (n) 很大,概率分布就会保持钟形。为了说明这一点,请考虑以下两种情况(当 p = 0.2 和 p = 0.8 时)。
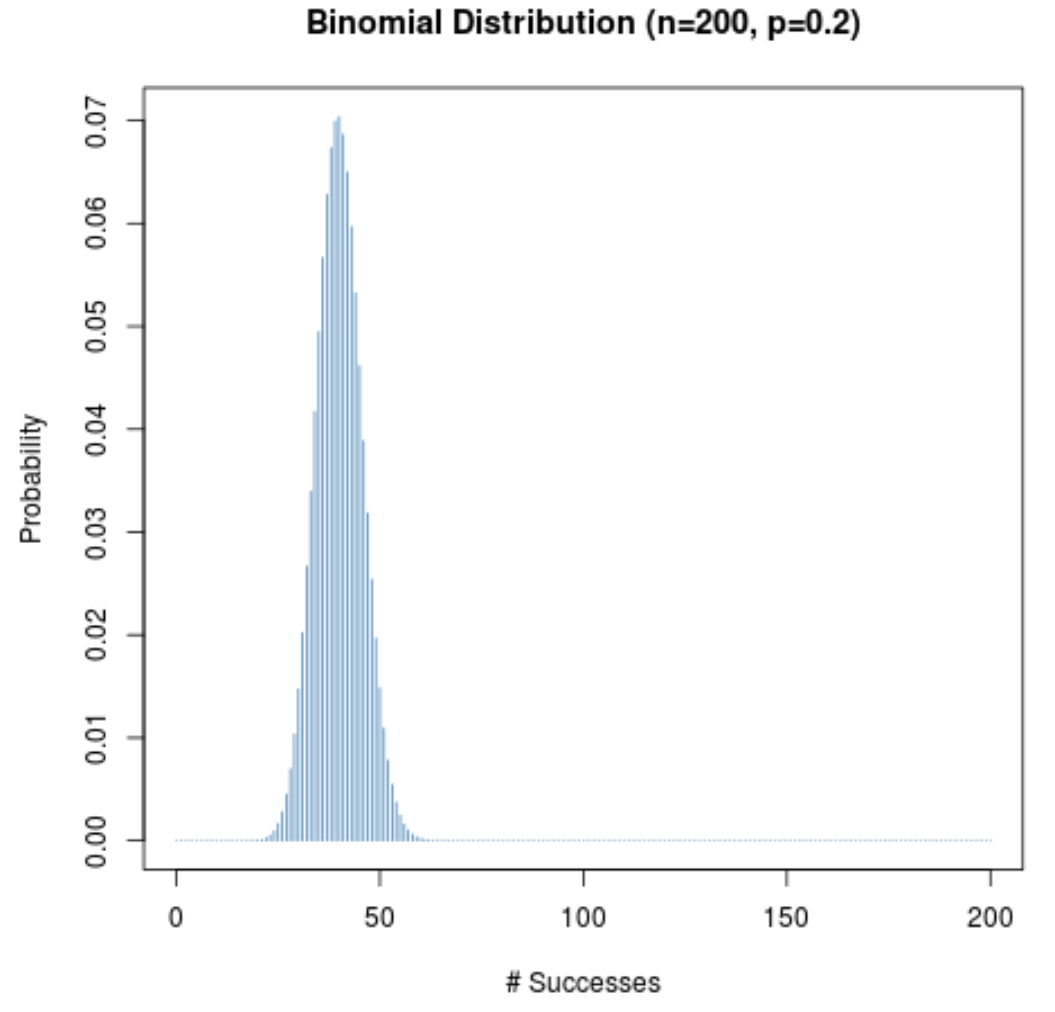
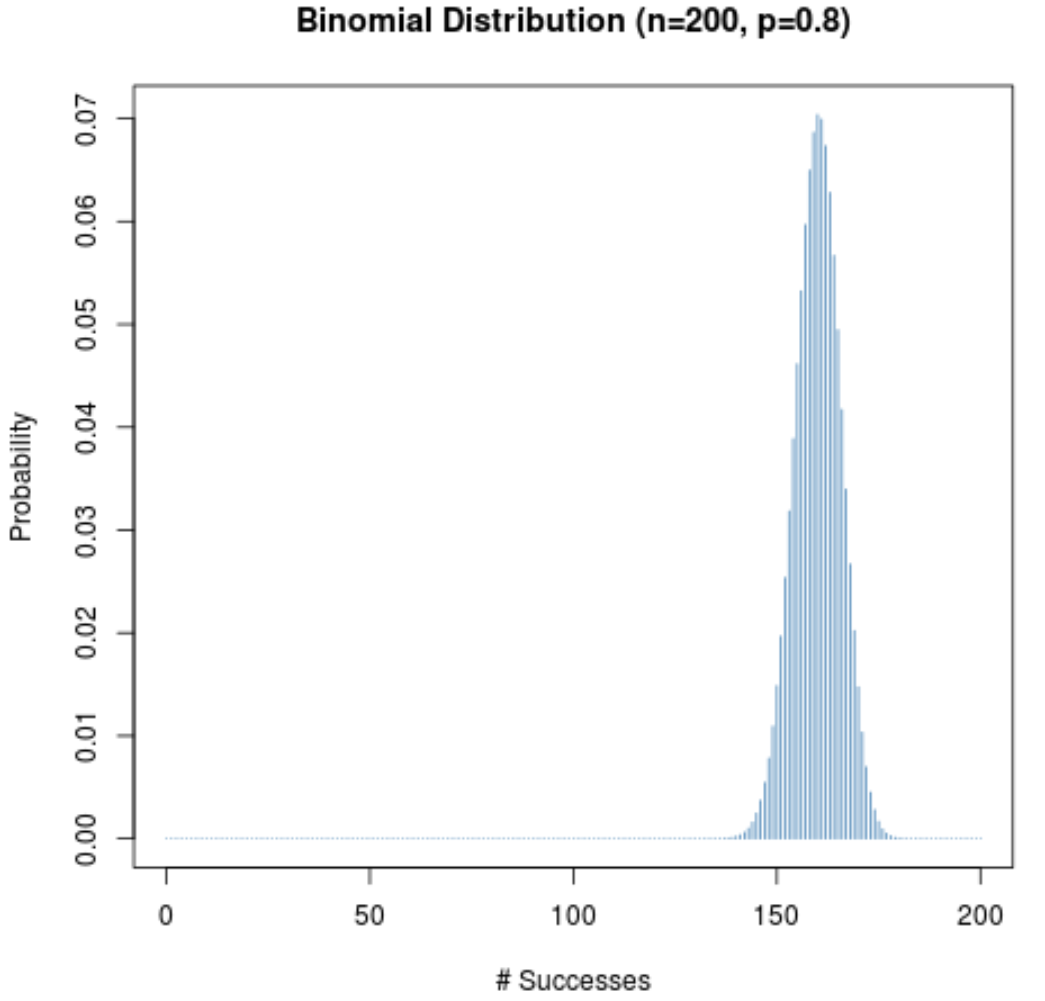
请注意这两种情况下概率分布都是钟形的。
示例 2:成功概率 (p) 接近 0.5
下图显示了 n = 10且 p = 0.4时的概率分布。
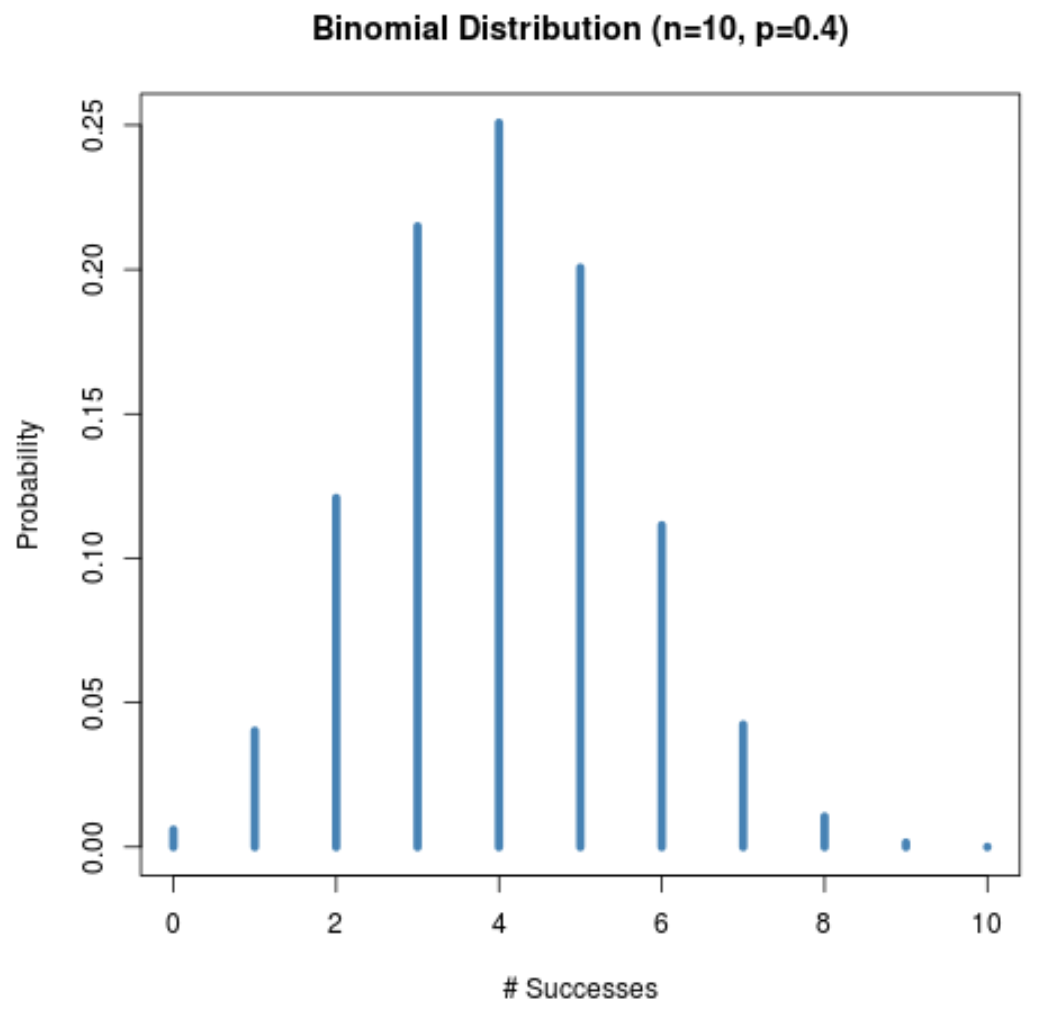
尽管样本量 (n = 10) 很小,但概率分布仍然呈钟形,因为给定试验的成功概率 (p = 0.4) 接近 0.5。
示例 3:偏态二项式分布
当(1)样本量较大或(2)给定试验的成功概率均不接近 0.5 时,二项式概率分布将向左或向右倾斜。
例如,下图显示了 n = 20且 p = 0.1时的概率分布。
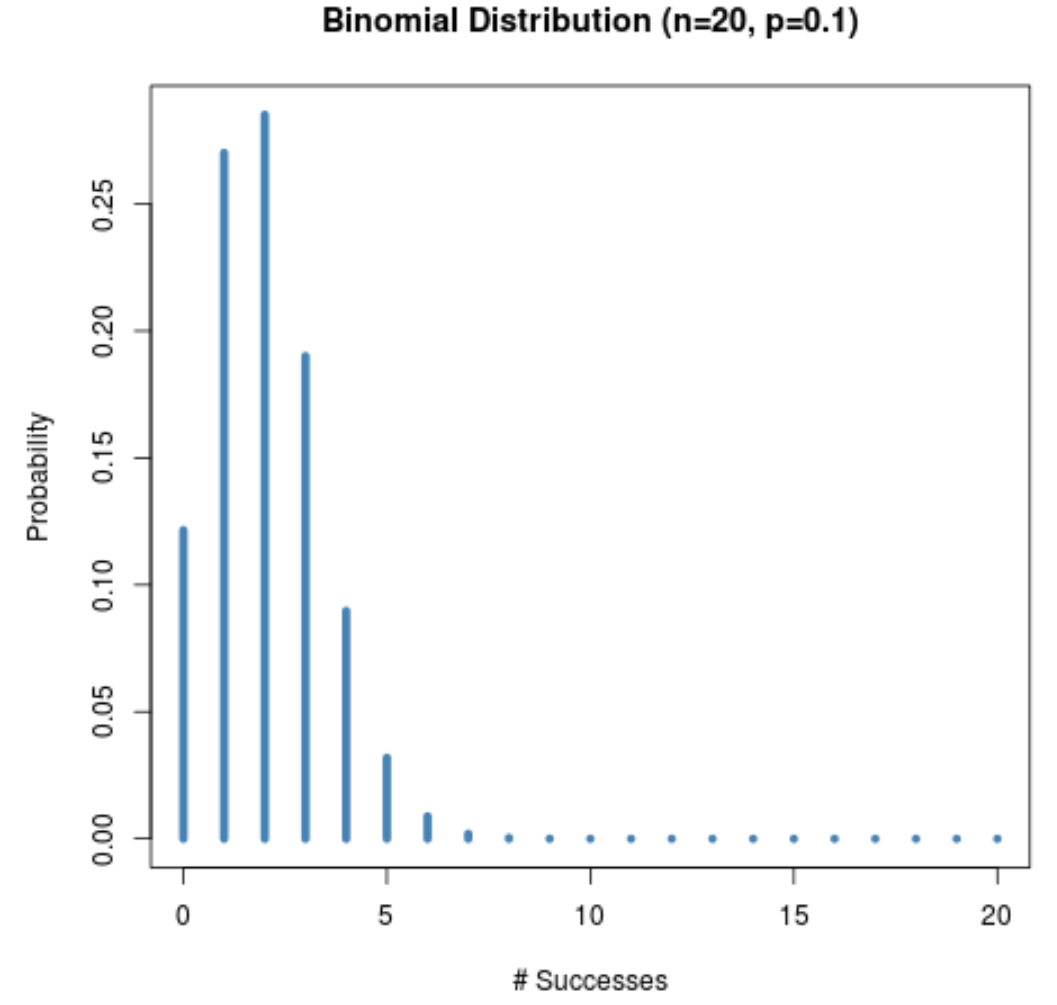
请注意分布如何向右倾斜。
下图显示了 n = 20且 p = 0.9时的概率分布。
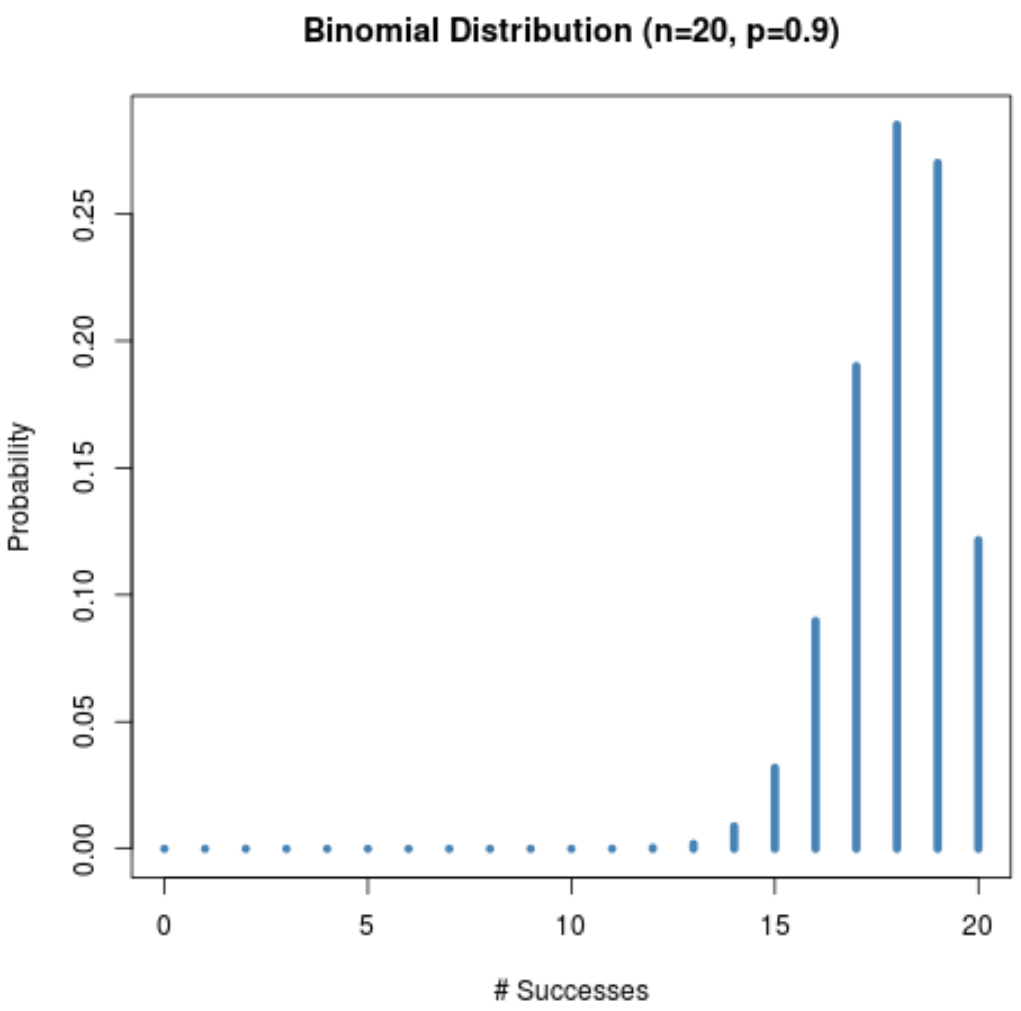
请注意分布是如何向左倾斜的。
尾注
本文中的每个图表都是使用 R 统计编程语言创建的。使用本教程了解如何在 R 中绘制您自己的二项式概率分布。