如何在 python 中使用二项式分布

二项式分布是统计学中最常用的分布之一。它描述了在n次二项式实验中获得k次成功的概率。

如果随机变量X服从二项式分布，则X = k成功的概率可以通过以下公式求出：

P(X=k) = _n C _k * p ^k * (1-p) ^nk

金子：

• n：试验次数
• k：成功次数
• p：给定试验的成功概率
• _n C _k ：在n次试验中获得k次成功的方法数

本教程介绍如何在 Python 中使用二项式分布。

如何生成二项式分布

您可以使用 numpy 库的random.binomial函数生成遵循二项分布的值数组：

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

结果表中的每个数字代表10 次试验过程中遇到的“成功”次数，其中给定试验的成功概率为0.25 。

如何使用二项分布计算概率

您还可以使用 scipy 库的binom 函数回答有关二项式概率的问题。

问题 1：内森的罚球命中率为 60%。如果他罚球 12 次，他罚中 10 次的概率是多少？

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

Nathan 恰好罚球 10 次的概率是0.0639 。

问题 2： Marty 抛一枚均匀的硬币 5 次。硬币正面朝上两次或更少的概率是多少？

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

硬币正面朝上 2 次或更少的概率为0.5 。

问题 3：我们知道 70% 的人支持某项法律。如果随机选择 10 个人，其中 4 到 6 人支持该法律的概率是多少？

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

4 到 6 名随机选择的个人支持该法律的概率为0.3398 。

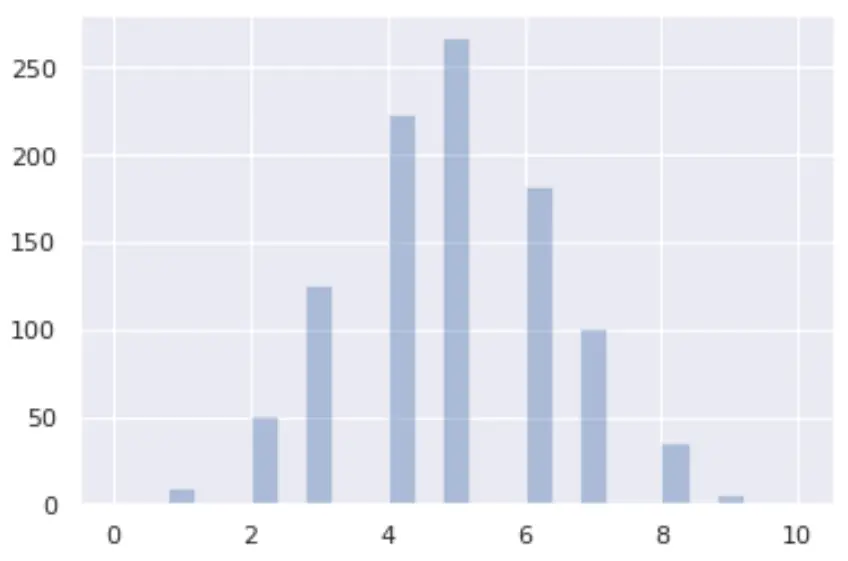
如何可视化二项式分布

您可以使用seaborn和matplotlib库在 Python 中可视化二项式分布：

 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

茶