伽马分布

经过本杰明·安德森博 8月 3, 2023 可能性 0 条评论

本文解释了什么是伽玛分布及其用途。因此，您将找到伽马分布的定义、其属性及其图形表示形式。

什么是伽马分布？

伽马分布是由两个特征参数 α 和 λ 定义的连续概率分布。换句话说，伽马分布取决于其两个参数的值：α 是形状参数，λ 是尺度参数。

伽马分布的符号是大写希腊字母 Г。因此，如果随机变量服从伽玛分布，则可以写成如下：

$X\sim \Gamma(\alpha,\lambda)$

伽玛分布还可以使用形状参数 k = α 和反比例参数 θ = 1/λ 进行参数化。在所有情况下，定义伽玛分布的两个参数都是正实数。

通常，伽玛分布用于对右偏数据集进行建模，以便图表左侧的数据更加集中。例如，伽玛分布用于对电气元件的可靠性进行建模。

伽马分布图

伽玛分布的图形取决于其特征参数的值。下面您可以看到伽马分布的密度函数如何根据形状参数和尺度参数而变化。

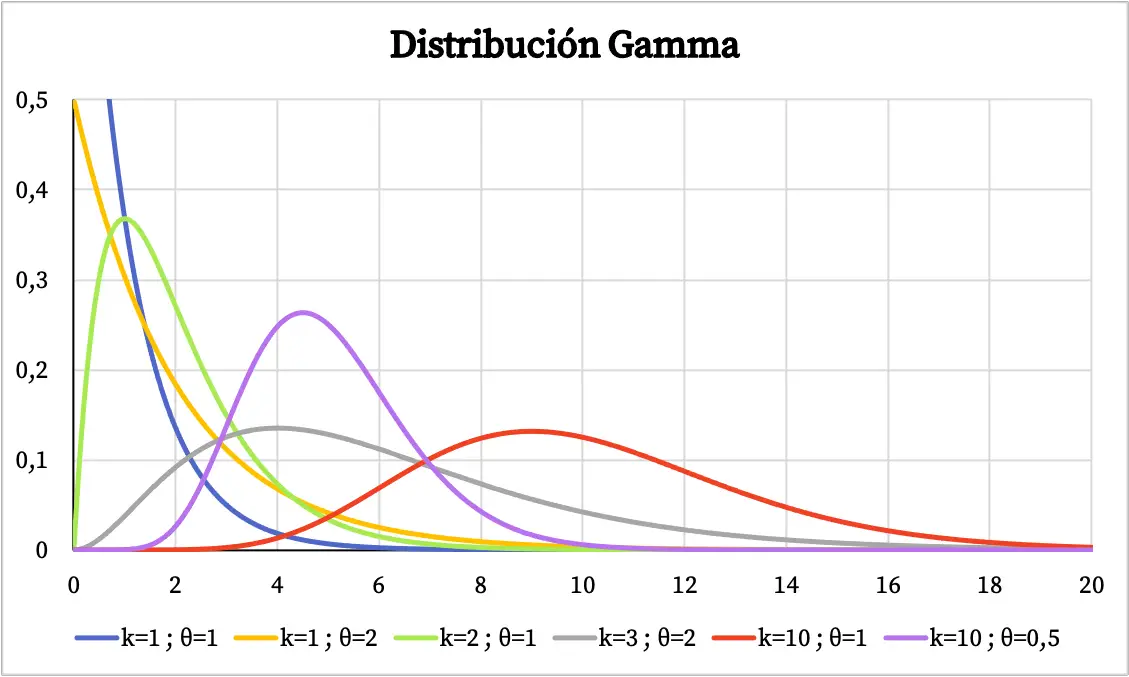
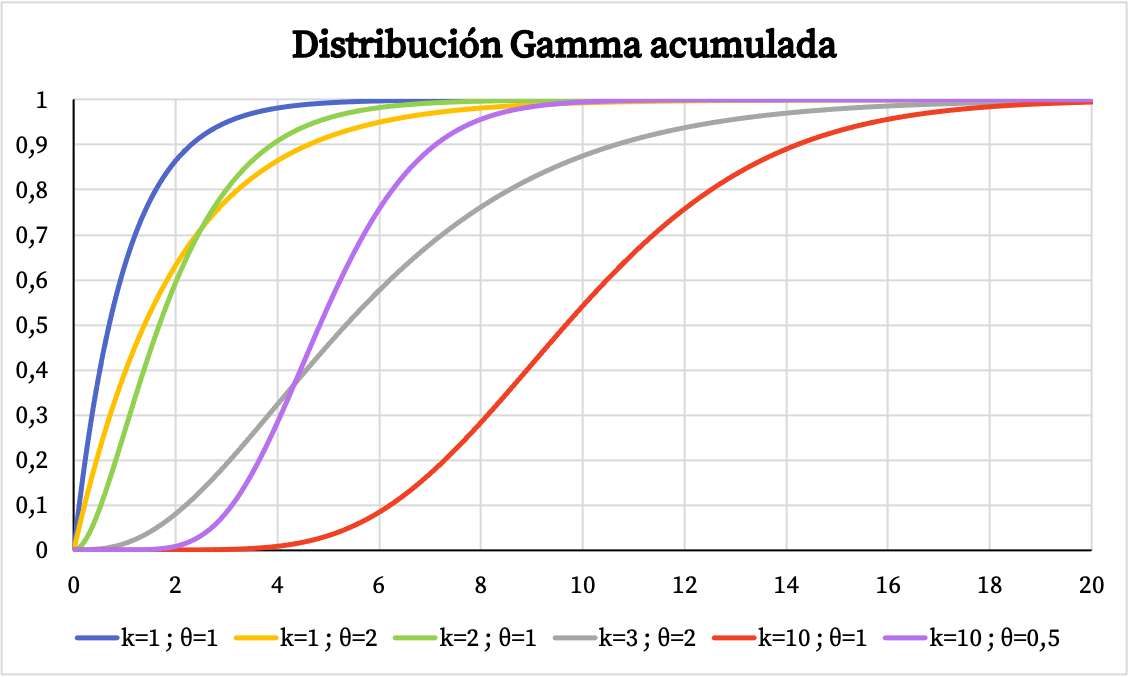
另一方面，您可以看到下面的伽玛分布的累积概率函数图：

伽玛分布的特征

接下来我们就来看看伽玛分布的特点是什么。

伽马分布图完全由其两个特征参数定义：α 是形状参数，λ 是尺度参数。

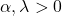
$\alpha , \lambda >0″ title=”Rendered by QuickLaTeX.com” height=”16″ width=”62″ style=”vertical-align: -4px;”></p> </p> <ul> <li>伽玛分布的域仅由正数组成。</li> </ul> <p class=$ $x\in (0,+\infty)$

伽玛分布的均值等于形状参数和尺度参数之间的比率，即α/λ。

$E[X]=\cfrac{\alpha}{\lambda}$

伽玛分布的方差等于形状参数除以尺度参数的平方。

$Var(X)=\cfrac{\alpha}{\lambda^2}$

对于小于 1 的 α 值，众数为 0。但如果 α 等于或大于 1，则伽马分布的众数可以通过以下公式计算：

$\begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}$

伽玛分布的密度函数的公式为：

$\displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}$

其中 Γ 为伽玛函数，定义为：

$\displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt$

由伽玛分布定义的随机变量的累积分布的公式如下：

$\displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy$

如果形状参数 α 等于 1，则伽玛分布相当于具有相同尺度参数 λ 的指数分布。

$X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)$

当尺度参数 λ 为平均值时，伽马分布是卡方分布的特例。

$\displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2$

关于作者

本杰明·安德森博

大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多

什么是伽马分布？

伽马分布图

伽玛分布的特征

关于作者

本杰明·安德森博

添加评论