如何在 r 中执行 cramer-von mises 检验（附示例）

Cramer-Von Mises 检验用于确定样本是否来自正态分布。

这种类型的检验对于确定给定数据集是否来自正态分布非常有用，这是许多统计检验中常用的假设，包括 回归、 方差分析、 t 检验等。 ‘其他的。

我们可以使用 R 中goftest包中的cvm.test()函数轻松执行 Cramer-Von Mises 测试。

下面的例子展示了如何在实际中使用这个功能。

示例 1：对正态数据进行 Cramer-Von Mises 检验

以下代码显示如何对样本大小 n=100 的数据集执行 Cramer-Von Mises 测试：

 library (goftest)

#make this example reproducible
set. seeds (0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Cramer-Von Mises test for normality
cvm. test (data, ' pnorm ')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:data
omega2 = 0.078666, p-value = 0.7007

测试的 p 值为0.7007 。

由于该值不小于0.05，我们可以假设样本数据来自正态分布的总体。

这个结果应该不足为奇，因为我们使用rnorm()函数生成样本数据，该函数根据标准正态分布生成随机值。

相关： R 中 dnorm、pnorm、qnorm 和 rnorm 指南

我们还可以生成直方图来直观地验证样本数据是否呈正态分布：

 hist(data, col=' steelblue ') 

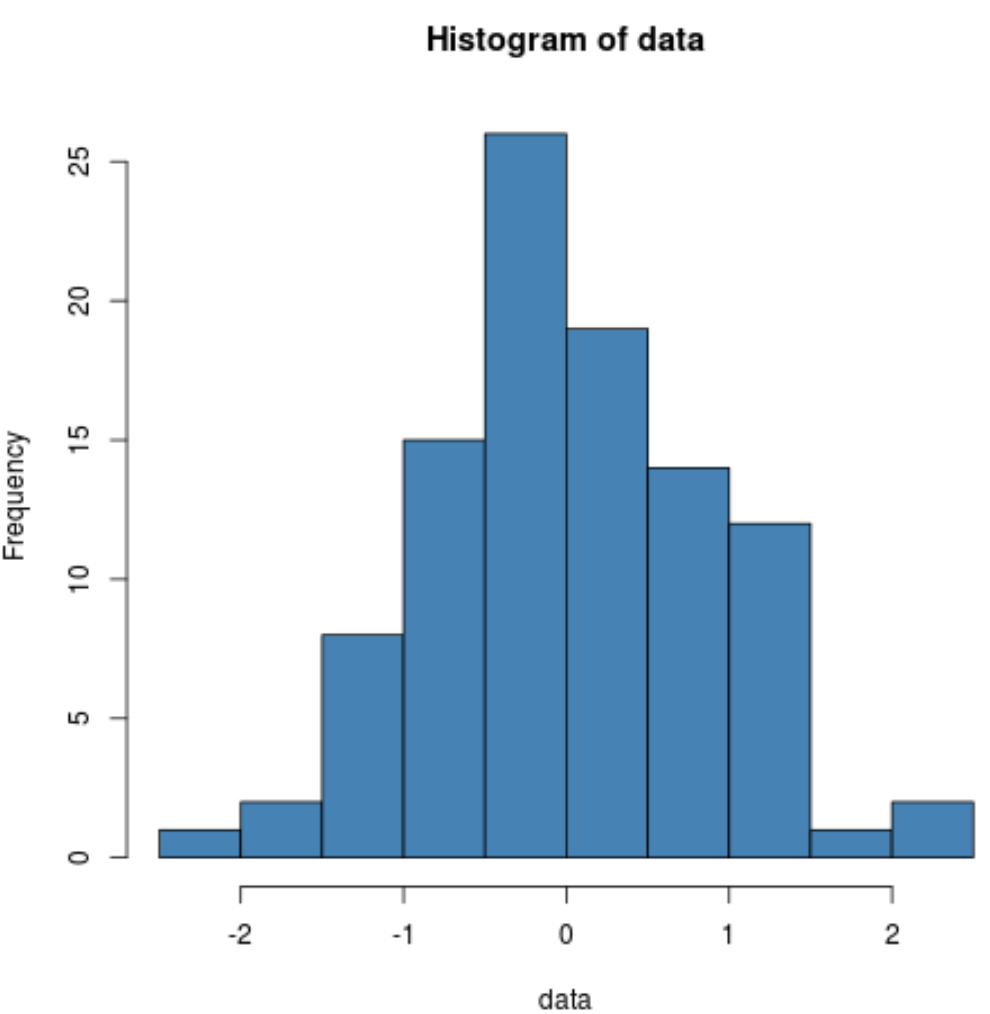
我们可以看到，分布呈钟形，峰值位于分布中心，这是正态分布数据的典型特征。

示例 2：非正态数据的 Cramer-Von Mises 检验

以下代码展示了如何对样本大小为 100 的数据集执行 Cramer-Von Mises 测试，其中值是根据泊松分布随机生成的：

 library (goftest)

#make this example reproducible
set. seeds (0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Cramer-Von Mises test for normality
cvm. test (data, ' pnorm ')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:data
omega2 = 27.96, p-value < 2.2e-16

测试的 p 值非常低。

由于该值小于 0.05，因此我们有足够的证据表明样本数据并非来自正态分布总体。

这个结果应该不足为奇，因为我们使用rpois()函数生成样本数据，该函数根据泊松分布生成随机值。

相关： R 中的 dpois、ppois、qpois 和 rpois 指南

我们还可以制作一个直方图来直观地看出样本数据不是正态分布的：

 hist(data, col=' coral2 ') 

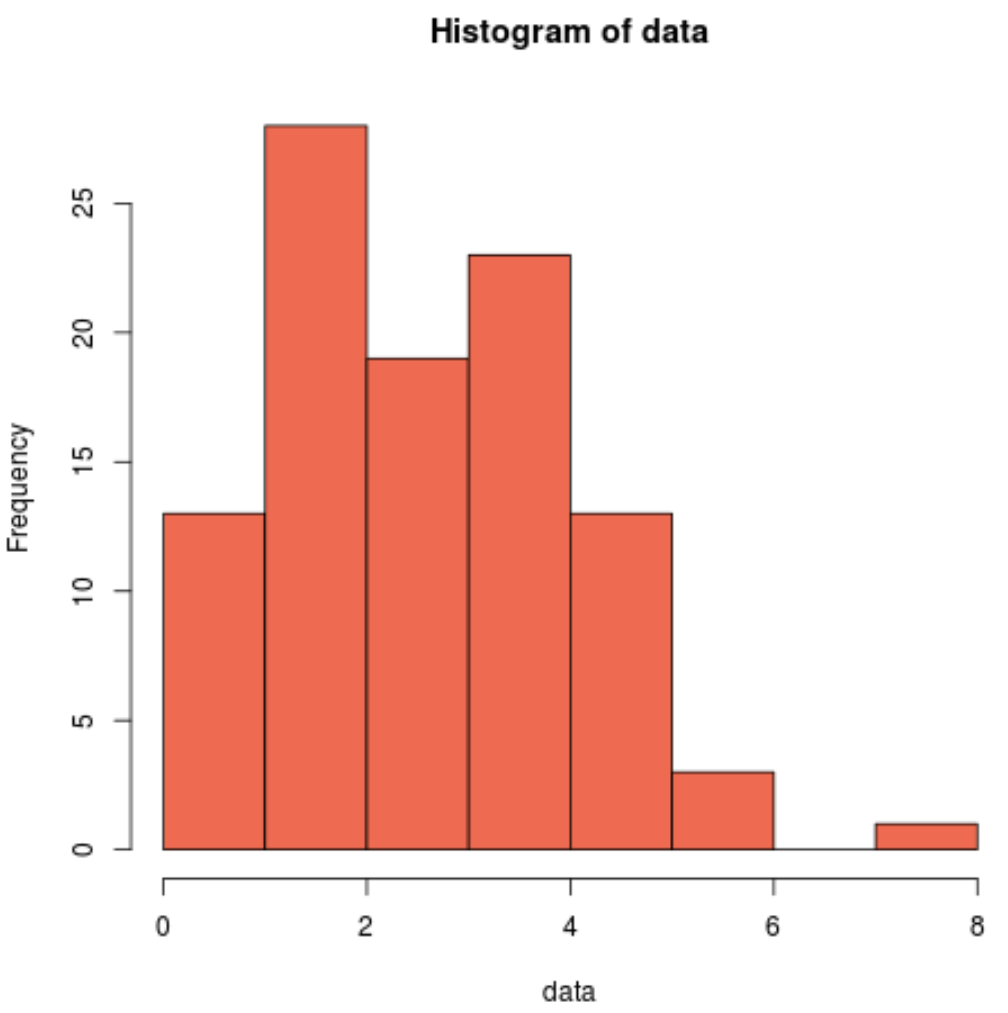
我们可以看到该分布是右偏的，并且不具有与正态分布相关的典型“钟形”。

因此，我们的直方图与 Cramer-Von Mises 检验的结果相匹配，并确认我们的样本数据并非来自正态分布。

如何处理非正态数据

如果给定的数据集不是正态分布的，我们通常可以执行以下转换之一以使其更正态分布：

1. 对数变换：将响应变量从 y 变换为log(y) 。

2. 平方根变换：将响应变量从 y 变换为√y 。

3. 立方根变换：将响应变量从 y 变换为y ^1/3 。

通过执行这些变换，响应变量通常近似正态分布。

请参阅 本教程以了解如何在实践中执行这些转换。

其他资源

以下教程解释了如何在 R 中执行其他正态性检验：

如何在 R 中执行 Shapiro-Wilk 检验
如何在 R 中执行 Anderson-Darling 测试
如何在 R 中执行 Kolmogorov-Smirnov 检验