几何平均值

在本文中，我们将解释什么是几何平均数、如何计算几何平均数以及几何平均数和算术平均数之间的区别。您还可以看到几何平均值的逐步求解练习以及此类平均值的属性。最后，您将找到一个计算器来计算任何数据集的几何平均值。

几何平均数是多少？

几何平均值是描述性统计中心性的度量。一组统计数据的几何平均值等于所有值乘积的n次方根。

几何平均数在商业金融中用于计算回报率、平均百分比和复利。

因此，几何平均值的公式如下：

只有当样本中的所有数据均为正数时，才能计算几何平均值。因为如果值为负，则根将有负解或无解，另一方面，如果数据为零，则数据相乘将得到零，因此几何平均值将等于 0。

几何平均数并不是唯一存在的平均数，还有算术平均数、加权平均数、平方平均数和调和平均数。

几何平均数与算术平均数的区别

几何平均数与算术平均数的主要区别在于，几何平均数对极值的敏感度不如算术平均数。另外，算术平均值可以用负值和零值来计算，而几何平均值只能用正值来计算。

同样，对于同一数据集，几何平均值通常低于算术平均值。

还应该指出的是，几何平均值的计算更为复杂，因此其统计意义更难以解释。

简而言之，与算术平均相比，几何平均有优点和缺点，并且根据数据的性质，计算这个或那个平均值是合适的。

如何计算几何平均值

要计算几何平均值，必须执行以下步骤：

1. 计算样本中所有统计数据的乘积。
2. 求计算出的乘积的 n 次方根。
3. 所得结果为统计样本的几何平均值。

正如您所看到的，使用计算器或计算机程序查找一组数据的几何平均值相对简单，因为您只需要计算乘积和根。相反，手工计算是相当费力的。

👉这就是为什么我们建议使用下面的计算器来计算数据集的几何平均值。

几何平均数示例

一旦我们了解了几何平均值的理论，我们将做一个示例，以便您可以准确地了解如何获得几何平均值。

• 公司过去五年的经济业绩是已知的。第一年，公司实现了10%的经济利润，第二年，利润达到23%，第三年，赚到的钱是16%，第四年，实现了7%的经济利润，投资第五年的回报率为 20%。您需要计算所有百分比的平均值。

正如我们所看到的，计算百分比的平均值时，不应使用算术平均值，而应使用几何平均值进行计算。

因此，我们应用几何平均公式：

我们将示例值代入公式并进行计算：

请注意，我们有五个数据点，因此我们正在计算五次方根。

几何平均数的数值结果为1.15，这意味着该公司每年的经济增长率为15%。

请记住，我们能够获得几何平均值，因为所有值都是正数，但如果任何百分比为负数，我们就必须将数据作为带有整数部分的正小数放入公式中。等于零。例如，-30%的增长应在公式中表示为0.70（1-0.3=0.7）。

几何平均值计算器

将任何样本统计数据插入下面的计算器即可找到其几何平均值。数据必须用空格分隔，并使用句点作为小数点分隔符输入。请记住，如果值为负或零，则无法确定几何平均值。

几何平均数的性质

几何平均数具有以下特点：

• 这是一种平均值，对于查找百分比或指数的平均值非常有用。

• 只有所有数据均为正数时才能计算。

• 两个数a和b的几何平均值的几何意义是与边长为a和b的矩形面积相同的正方形的边长。

• 三个数a 、 b和c的几何平均值的几何意义是体积等于边长a 、 b和c的平行六面体的立方体的边长。

• 一组数据的几何平均值的对数给出了同一组数据的对数的算术平均值。

• 一组值的几何平均值总是小于或等于算术平均值。

• 加权几何平均数的计算方式与几何平均数相同，但通过在每个数据项的指数上加上权重来对统计值进行加权。

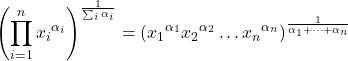
在Excel中计算几何平均值

最后，让我们看看如何使用 Excel 程序查找数据集的几何平均值。

要在Excel中计算几何平均值，您需要使用MEANS.GEOM函数。只需输入所有想要取几何平均值的值，函数就会返回几何平均值结果。

例如，要确定上面示例的几何平均值，您必须在 Excel 框中写入=MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) 。

您应该记住，如果任何值为零或负数，该函数将返回错误。

正如您所看到的，使用 Excel 计算几何平均值要简单快捷得多，因为您只需将数据复制到工作表上并使用公式即可。