分类树和回归树简介

当一组预测变量和响应变量之间的关系是线性时，多元线性回归等方法可以生成准确的预测模型。

然而，当一组预测变量和响应之间的关系高度非线性且复杂时，非线性方法可能会表现更好。

非线性方法的一个例子是分类树和回归树，通常缩写为CART 。

顾名思义，CART 模型使用一组预测变量来创建预测响应变量值的决策树。

例如，假设我们有一个数据集，其中包含数百名职业棒球运动员的预测变量“打球年数”和“平均本垒打”以及响应变量“年薪” 。

该数据集的回归树可能如下所示：

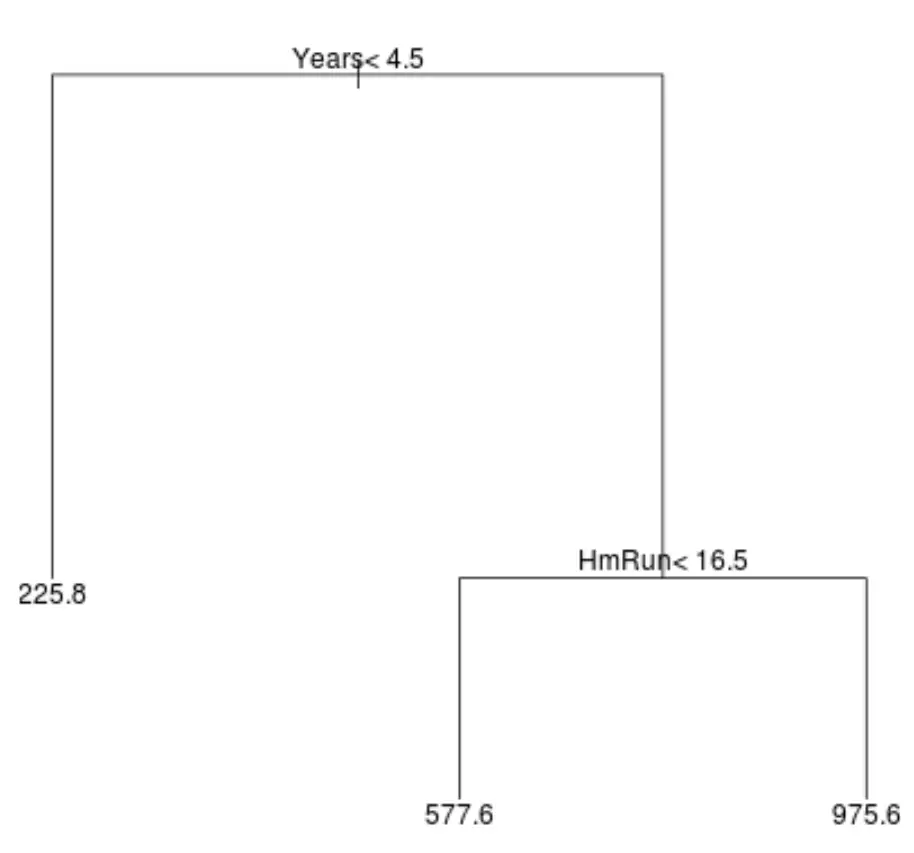
解释树的方式如下：

• 打球时间少于 4.5 年的球员预计薪水为 225,800 美元。
• 平均打球时间超过 4.5 年且本垒打少于 16.5 个的球员的预计工资为 577,600 美元。
• 拥有 4.5 年或以上比赛经验且平均 16.5 个本垒打或以上的球员的预期薪水为 $975.6K。

这个模型的结果直观上应该是有意义的：拥有更多年经验和更多平均本垒打的球员往往会获得更高的薪水。

然后我们可以使用这个模型来预测新球员的薪水。

例如，假设某位球员已经打了 8 年球，平均每年打出 10 个本垒打。根据我们的模型，我们预测该球员的年薪为 577,600 美元。

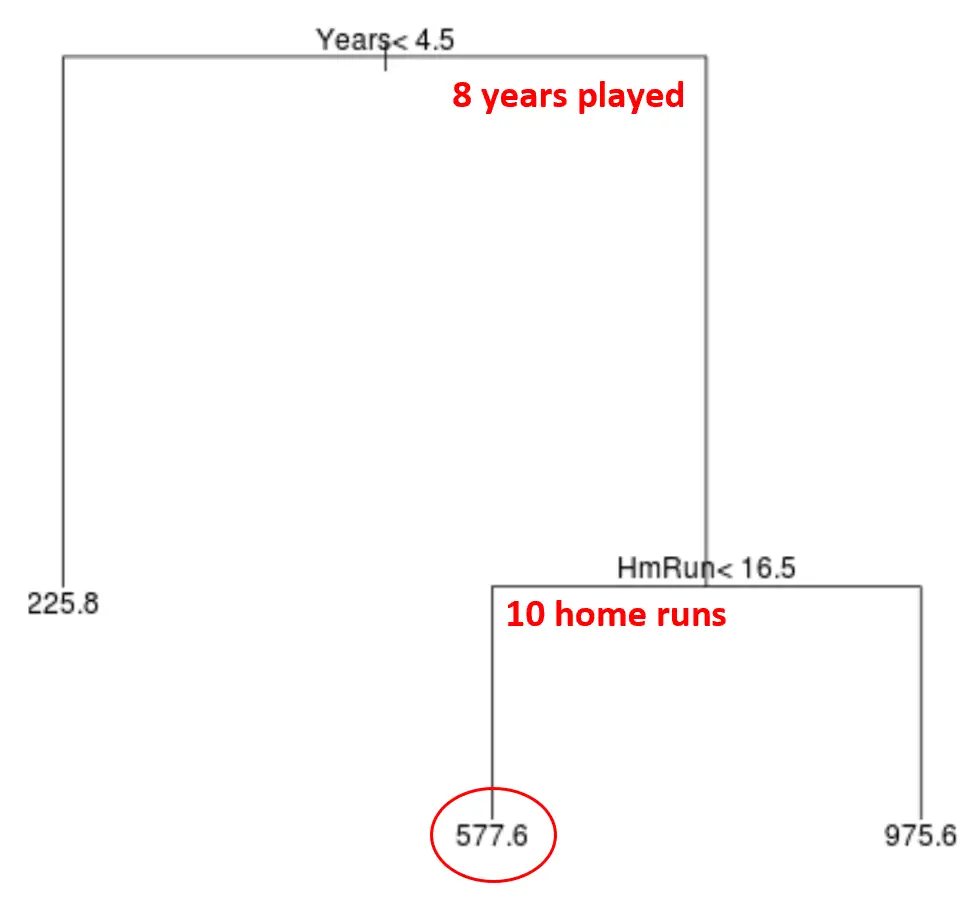
关于树的一些评论：

• 位于树顶部的第一个预测变量是最重要的，也就是说，它对响应变量值的预测影响最大。在这种情况下，打球的年份比巡回赛的平均水平更能预测工资。
• 树底部的区域称为叶节点。该特定树具有三个终端节点。

创建 CART 模型的步骤

我们可以使用以下步骤为给定的数据集创建 CART 模型：

步骤 1：使用递归二元分裂在训练数据上生长一棵大树。

首先，我们使用一种称为递归二分分裂的贪心算法来使用以下方法来生长回归树：

• 考虑所有预测变量 X _{1 、} X ₂ 、…（残余标准误差）最低。 。
  • 对于分类树，我们选择预测器和切点，以使生成的树具有最低的分类错误率。
• 重复此过程，仅当每个终端节点的观测值少于某个最小数量时才停止。

该算法是贪婪的，因为在树构建过程的每个步骤中，它仅根据该步骤确定要进行的最佳分割，而不是展望未来并选择将在未来阶段产生更好的树全局的分割。

步骤 2：对大树应用成本复杂度剪枝，以获得基于 α 的最佳树序列。

一旦我们长出了大树，我们就需要使用一种称为复杂修剪的方法来修剪它，其工作原理如下：

• 对于每个可能的具有 T 个终端节点的树，找到最小化 RSS + α|T| 的树。
• 请注意，当我们增加 α 的值时，具有更多终端节点的树会受到惩罚。这确保了树不会变得太复杂。

这个过程会产生每个 α 值的最佳树序列。

步骤3：使用k折交叉验证来选择α。

一旦我们找到每个 α 值的最佳树，我们就可以应用k 折交叉验证来选择使测试误差最小化的 α 值。

第四步：选择最终的模板。

最后，我们选择最终模型作为与所选 α 值相对应的模型。

CART模型的优缺点

CART 模型具有以下优点：

• 它们很容易解释。
• 它们很容易解释。
• 它们很容易形象化。
• 它们可以应用于回归和分类问题。

然而，CART模型有以下缺点：

• 它们的预测准确性往往不如其他非线性机器学习算法。然而，通过使用 bagging、boosting 和随机森林等方法对许多决策树进行聚类，可以提高其预测准确性。

相关：如何在 R 中拟合分类和回归树