双向方差分析:定义、公式和示例
双向方差分析(“方差分析”)用于确定分配给两个变量(有时称为“因子”)的三个或更多独立组的平均值之间是否存在统计显着差异。
本教程解释了以下内容:
- 何时使用双向方差分析。
- 执行双向方差分析必须满足的假设。
- 如何执行双向方差分析的示例。
何时使用双向方差分析
当您想了解两个因素如何影响响应变量以及两个因素对响应变量是否存在交互作用时,您应该使用双向方差分析。
例如,假设植物学家想要探索阳光照射和浇水频率如何影响植物生长。她种下了 40 颗种子,让它们在不同的阳光照射和浇水频率条件下生长两个月。两个月后,她记录了每株植物的高度。
在这种情况下,我们有以下变量:
- 响应变量:植物生长
- 因素:阳光照射、浇水频率
我们想回答以下问题:
- 阳光照射会影响植物生长吗?
- 浇水频率会影响植物生长吗?
- 阳光照射和浇水频率之间是否存在交互作用? (例如,阳光照射对植物的影响取决于浇水频率)
我们将使用双向方差分析进行此分析,因为我们有两个因素。相反,如果我们想知道浇水频率对植物生长的影响有多大,我们将使用单向方差分析,因为我们只处理一个因素。
双向方差分析的假设
为了使双向方差分析的结果有效,必须满足以下假设:
1. 正态性– 每个组的响应变量近似呈正态分布。
2. 方差相等——每组的方差应大致相等。
3. 独立性——各组内的观察结果彼此独立,并且组内的观察结果是通过随机抽样获得的。
双向方差分析:示例
植物学家想知道植物生长是否受到阳光照射和浇水频率的影响。她种下了 40 颗种子,让它们在不同的阳光照射和浇水频率条件下生长两个月。两个月后,她记录了每株植物的高度。结果如下所示:

在上表中,我们看到每种条件组合下都生长了五株植物。
例如,每天浇水且没有阳光的情况下种植五株植物,两个月后它们的高度分别为 4.8 英寸、4.4 英寸、3.2 英寸、3.9 英寸和 4.4 英寸:

她在 Excel 中执行双向方差分析并获得以下结果:
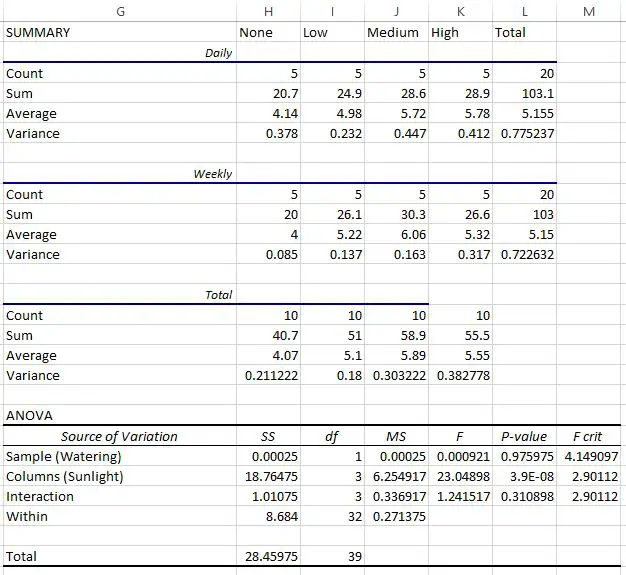
最后一个表显示了双向方差分析的结果。我们可以观察到以下几点:
- 浇水频率和阳光照射之间相互作用的 p 值为0.310898 。这在 0.05 alpha 水平上并不具有统计显着性。
- 浇水频率的 p 值为0.975975 。这在 0.05 alpha 水平上并不具有统计显着性。
- 阳光照射的 p 值为3.9E-8 (0.000000039) 。这在 0.05 的 alpha 水平下具有统计显着性。
这些结果表明,阳光照射是对植物高度具有统计显着影响的唯一因素。
而且由于不存在交互作用,因此阳光照射的效果在每个浇水频率水平上都是一致的。
简而言之,植物每天还是每周浇水对于阳光照射对植物的影响没有影响。
其他资源
以下文章解释了如何使用不同的统计软件执行双向方差分析:
如何在 Excel 中执行双向方差分析
如何在 R 中执行双向方差分析
如何在 Python 中执行双向方差分析
如何在 SPSS 中执行双向方差分析
如何在 Stata 中进行双向方差分析