后验概率：定义+示例

后验概率是考虑新信息后事件发生的更新概率。

例如，我们可能对在考虑了刚刚发生的事件“B”之后发生事件“A”的概率感兴趣。我们可以使用以下公式计算后验概率：

P(A|B) = P(A) * P(B|A) / P(B)

金子：

P(A|B) = 假设事件 B 已发生，则事件 A 发生的概率。请注意“| » 意思是“给予”。

P(A) = 事件 A 发生的概率。

P(B) = 事件 B 发生的概率。

P(B|A) = 假设事件 A 已发生，则事件 B 发生的概率。

示例：计算后验概率

森林由 20% 的橡树和 80% 的枫树组成。假设我们知道 90% 的橡树是健康的，而只有 50% 的枫树是健康的。假设，从远处看，您可以看出一棵特定的树是健康的。这棵树是橡树的概率是多少？

回想一下，在事件 B 发生的情况下，事件 A 发生的概率为：

P(A|B) = P(A) * P(B|A) / P(B)

在此示例中，假设树是健康的，则该树是橡树的概率为：

P(橡木|健康) = P(橡木) * P(健康|橡木) / P(健康)

P(Oak) = 给定树是橡树的概率为0.2 ，因为森林中所有树的 20% 是橡树。

P(健康) = 给定树健康的概率可计算如下： (0.20)*(0.9) + (0.8)*(0.5) = 0.58 。

P(Healthy|Oak) = 如果一棵树是橡树，那么它健康的概率为0.9 ，因为我们被告知 90% 的橡树都是健康的。

使用这三个数字，我们可以计算出这棵树是健康的橡树的概率：

P(橡木|健康) = P(橡木) * P(健康|橡木) / P(健康) = (0.2) * (0.9) / (0.58) = 0.3103 。

为了直观地理解这个概率，我们假设下面的网格代表这个由 100 棵树组成的森林。其中 20 棵树是橡树，其中 18 棵是健康的。其他 80 棵树是枫树，其中 40 棵很健康。

（O = 橡木，M = 枫木，绿色 = 健康，红色 = 不健康）

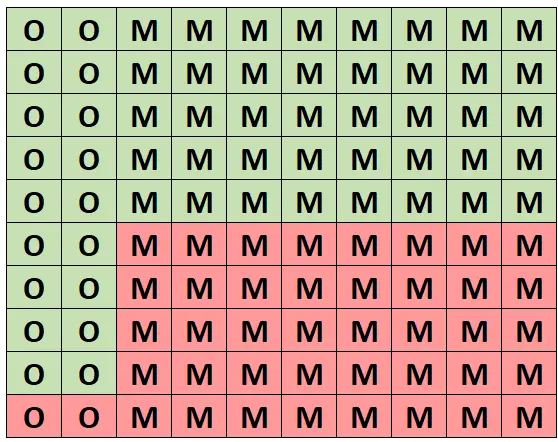
在所有树木中，恰好有 58 棵是健康的，其中 18 棵是橡树。因此，如果我们知道我们选择了一棵健康的树，那么它是橡树的概率是 18/58 = 0.3103 。

什么时候应该使用后验概率？

后验概率广泛应用于金融、医学、经济学和天气预报等领域。

使用后验概率的目的是在获得新信息后更新我们对某事的先验信念。

回想一下前面的例子，我们知道森林中一棵给定的树是橡树的概率是 20%。这称为先验概率。如果我们简单地随机选择一棵树，我们知道它是橡树的概率是 0.20。

然而，一旦我们获得了我们选择的树是健康的新信息，我们就能够使用这些新信息来确定这棵树是橡树的后验概率为 0.3103。

在现实世界中，人们不断发现新的信息。这些新信息帮助我们更新以前的信念。用统计学术语来说，这意味着我们能够生成发生事件的后验概率，这有助于我们更准确地了解世界，并使我们能够对未来事件做出更准确的预测。