四分位距（或四分位距）

本文解释什么是四分位距，也称为四分位距。您还可以通过具体示例了解如何计算四分位数范围。您将了解四分位数范围的用途以及与间隔的差异。此外，您可以使用在线计算器计算任何数据集的四分位数范围。

四分位距（或四分位距）是多少？

四分位距，也称为四分位距，是一种统计离散度的度量，表示第三个四分位数和第一个四分位数之间的差异。因此，要计算统计数据集的四分位距，必须首先找到第三和第一四分位数，然后将它们相减。

简而言之，四分位数范围由缩写 IQR 表示。

四分位距最有利的特征之一是它是一个稳健的统计量，即它对异常值具有很高的稳健性。由于四分位距的计算中没有考虑极值，因此如果出现新的异常值，其值变化很小。

显然，除了四分位距之外，还有其他离散度度量，最著名的度量是极差、方差、标准差、平均差和变异系数。

如何计算四分位距（或四分位距）

在统计学中，要计算数据集的四分位距（或四分位距），必须首先找到数据集的第一和第三四分位数，然后计算第三四分位数减去第一四分位数。

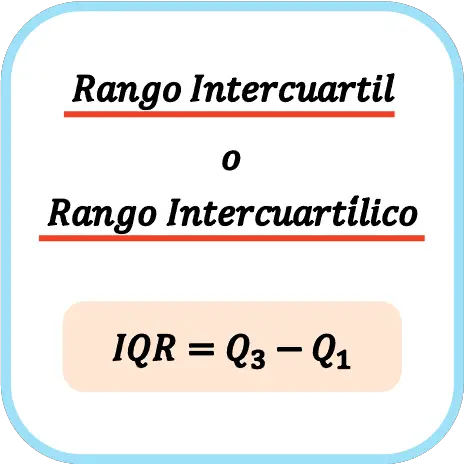
因此，四分位距或四分位距的计算公式为：

👉您可以使用下面的计算器来计算任何数据集的四分位数范围。

因此，了解如何计算统计样本的四分位数至关重要。这就是为什么我建议您在继续之前先查阅以下文章，然后继续进行解释。

四分位间距示例

给出了四分位距（或四分位距）的定义和公式，下面是一个已解决的练习，因此您可以准确地了解如何计算这种类型的离散度度量。

• 我们想要统计分析投资一家公司是否是个好主意。为此，我们收集了该公司过去 15 个月的股价数据。在下表中，您可以看到观察到的数据从最低到最高排序。计算该数据集的四分位数范围。

正如我们在上一节中看到的，要获得样本的四分位数范围（或四分位数范围），我们必须首先计算第一和第三四分位数。

第一个四分位数是前半部分值的中位数，相当于 8.95 欧元/股。

另一方面，第三个四分位数是后半部分值的中间值，因此为 9.83 欧元/股。

因此，要找到四分位数范围，只需应用公式并减去第三个四分位数减去第一个四分位数即可。

四分位数（或四分位数）范围计算器

在下面的计算器中输入一个统计数据集，即可计算其四分位距或四分位距。数据必须用空格分隔，并使用句点作为小数点分隔符输入。

四分位距和极差之间的区别

在统计学中，四分位距（或四分位距）和区间之间的差是执行计算时所取的值。四分位数极差是第三个四分位数与第一个四分位数之间的差，而极差是样本极值之间的差。

因此，四分位距使用中心数据来衡量样本的离散度，而间隔则使用极端数据来量化样本的离散度。

因此，统计范围更容易受到异常值的影响，因为它们通常代表数据集的最小值或最大值。因此，四分位距相对于区间的优点之一是它具有更大的鲁棒性。

四分位距（或四分位距）的用途是什么？

主要是，四分位距（或四分位距）用于衡量数据集的分布。尽管分析样本的分散性需要计算更多的统计度量，但四分位数范围提供了样本分散程度的想法，至少是中心值的分散程度。

因此，四分位距的解释相对简单。四分位距的值越大，说明样本中的中间数据越分散；四分位距越小，说明中间数据越接近。

此外，四分位数范围对于创建盒须图也很有用，这是一种广泛用于分析股票市场上的股票价格行为的图表。