圆形图
在本文中,您将了解什么是饼图、如何构建饼图以及此类图表的分步练习。此外,您还可以看到饼图的特点。
什么是饼图?
饼图,也称为饼图,是一种统计图表,用于直观地表示百分比和比例。更准确地说,在饼图中,数据由圆的部分表示,因此每个奶酪的角度与其频率成正比。
因此,某个值出现的频率越高,它在饼图中所占的份额就越大。

在统计学中,饼图对于在图形上表示定性数据非常有用,并且还可以让您快速得出结论。
应该注意的是,饼图有许多不同的名称,例如饼图、披萨图、饼图、奶酪图甚至 360 度图。
如何制作饼图
鉴于饼图的定义,本节展示如何创建这种类型的图表:
- 收集统计数据并准备相应的频数表。
- 用以下公式计算图形各扇形的角度
- 根据计算出的角度,使用量角器在圆形图上表示扇区。
- 使用以下公式计算每个部门的百分比:
- 在图表上标出每个部门的百分比。
![]()
金子
![]()
是扇区i的角度,
![]()
其绝对频率和
![]()
数据总数。
![]()
金子
![]()
是部门i的百分比,
![]()
其绝对频率和
![]()
数据总数。
饼图示例
为了让您了解圆形图表是如何构建的,我在下面提供了一个逐步解释的示例。
- 50 个人被问及他们最喜欢的城市,数据整理如下表。将这些统计数据绘制在饼图上。

首先你必须找到每个奶酪对应的角度。为此,我们应用以下公式:
![]()
金子
![]()
是每个扇形的角度,
![]()
它的频率和
![]()
观察总数。
例如,计算数据表中第一个值对应的角度:
![]()
一旦我们知道了角度,只需使用量角器来表示圆扇形:
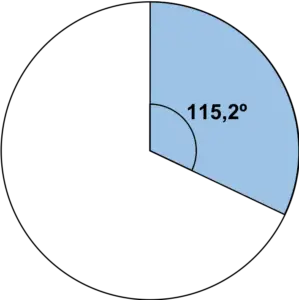
我们对表中的所有值重复相同的步骤:
![]()
![]()
![]()
![]()
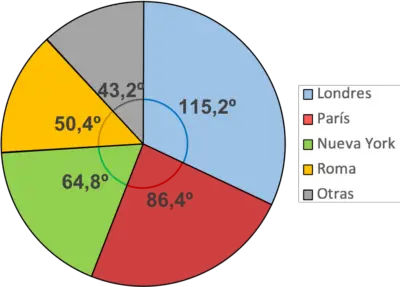
建议为每个扇区涂上颜色,以使图表更易于理解。同样,您应该添加图例来显示图表中每种颜色的含义。
在绘制奶酪图形后,我们需要计算每种奶酪的百分比并将其放在图表上。为此,我们使用以下公式:
![]()
金子
![]()
是每个部门的百分比,
![]()
它的频率和
![]()
统计研究的数据总数。
因此,每个部门的百分比为:
![]()
![]()
![]()
![]()
![]()
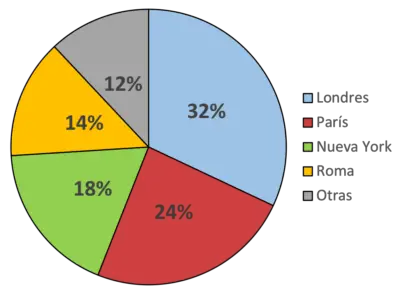
例如,通过此饼图,我们表明蓝色代表伦敦市,并且是大多数人喜欢的地方(32% 的人)。另一方面,绿色代表纽约,这是 18% 的受访者最喜欢的城市。
饼图功能
卡芒贝尔奶酪的特点如下:
- 饼图对于表示定性数据非常有用。
- 然而,还有其他类型的统计图更适合表示定量变量或时间序列。
- 此外,饼图中只能表示一个变量,因此很难比较变量。
- 饼图非常直观,可以快速分析和得出结论。
- 当扇区很多或有些扇区很小时,阅读图表会很困难。在这种情况下,建议将小扇区分组为一个名为“其他”的扇区。