如何在excel中计算p值（3个示例）

在统计学中，我们使用假设检验来确定有关总体参数的陈述是否正确。

当我们进行假设检验时，我们通常会得到 T 分数检验统计量。

一旦我们找到这个 t 得分检验统计量，我们就可以找到与之相关的 p 值。

如果该 p 值小于某个值（例如 0.10、0.05、0.01），则我们拒绝检验的原假设并得出结论：我们的结果具有统计显着性。

以下示例展示了如何在三种不同情况下在 Excel 中计算检验统计量的 p 值。

示例 1：计算双尾检验的 P 值

假设一位植物学家想知道某种植物的平均高度是否等于 15 英寸。

在 12 株植物的随机样本中，她发现样本的平均高度为 14.33 英寸，样本的标准差为 1.37 英寸。

它使用以下原假设和备择假设执行假设检验：

H ₀ （零假设）：μ= 15 英寸

H _A （替代假设）：μ ≠ 15 英寸

检验统计量计算如下：

• t = ( X – µ) / (s/ √n )
• t = (14.33-15) / (1.37/√ 12 )
• t = -1.694

与此检验统计量相关的自由度为 n-1 = 12-1 = 11 。

为了找到此检验统计量的 p 值，我们将在 Excel 中使用以下公式：

 =T.DIST.2T(ABS(-1.694), 11)

以下屏幕截图显示了如何在实践中使用该公式。

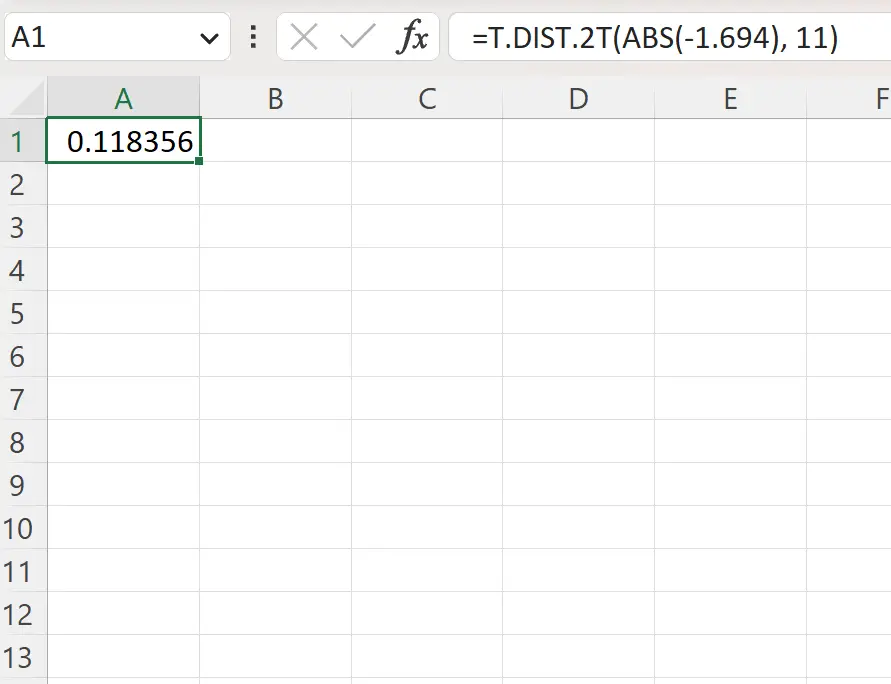
双尾 p 值为0.1184 。

由于这个值 不小于0.05，我们无法拒绝原假设。我们没有足够的证据表明平均植物高度不同于 15 英寸。

示例 2：计算左侧检验的 P 值

假设我们假设工厂生产的某个小玩意的平均重量是 20 克。然而，检查员估计实际平均重量不到 20 克。

为了测试这一点，它对 20 个小部件的简单随机样本进行了权衡，并获取以下信息：

• n = 20个小部件
• x = 19.8克
• s = 3.1克

然后，它使用以下原假设和备择假设执行假设检验：

H ₀ （零假设）：μ ≥ 20 克

H _A （替代假设）：μ < 20 克

检验统计量计算如下：

• t = ( X – µ) / (s/ √n )
• t = (19.8-20) / (3.1/√ 20 )
• t = -.2885

与此检验统计量相关的自由度为 n-1 = 20-1 = 19 。

为了找到此检验统计量的 p 值，我们将在 Excel 中使用以下公式：

 =T.DIST(-.2885, 19, TRUE)

以下屏幕截图显示了如何在实践中使用该公式。

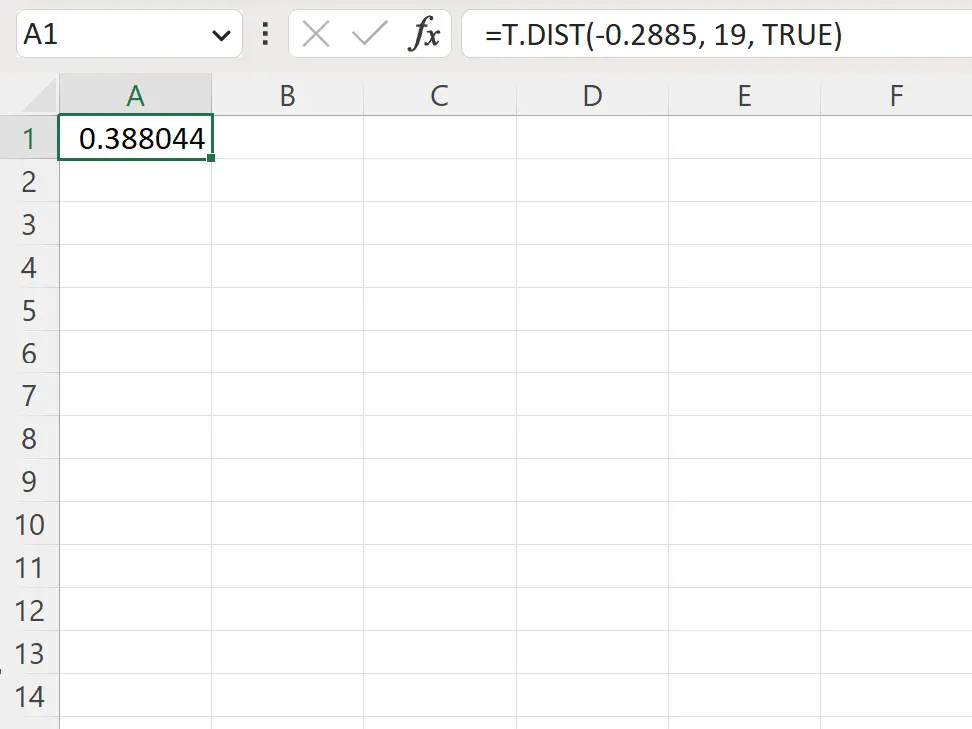
左侧的 p 值为0.388044 。

由于这个值 不小于 0.05，检验员未能拒绝原假设。没有足够的证据表明该工厂生产的小部件的实际平均重量不足20克。

注意：我们使用TRUE参数来指定计算 p 值时应使用累积分布函数。

示例 3：计算右尾检验的 P 值

假设某种植物的平均高度为 10 英寸。然而，一位植物学家表示，真正的平均高度超过 10 英寸。

为了验证这一说法，她测量了 15 株植物的简单随机样本的高度，并获得了以下信息：

• n = 15株植物
• x = 11.4英寸
• s = 2.5英寸

然后，它使用以下原假设和备择假设执行假设检验：

H ₀ （零假设）：μ ≤ 10 英寸

H _A （替代假设）：μ > 10 英寸

检验统计量计算如下：

• t = ( X – µ) / (s/ √n )
• t = (11.4-10) / (2.5/√ 15 )
• t = 2.1689

与此检验统计量相关的自由度为 n-1 = 15-1 = 14 。

为了找到此检验统计量的 p 值，我们将在 Excel 中使用以下公式：

 =T.DIST.RT(2.1689, 14)

以下屏幕截图显示了如何在实践中使用该公式。

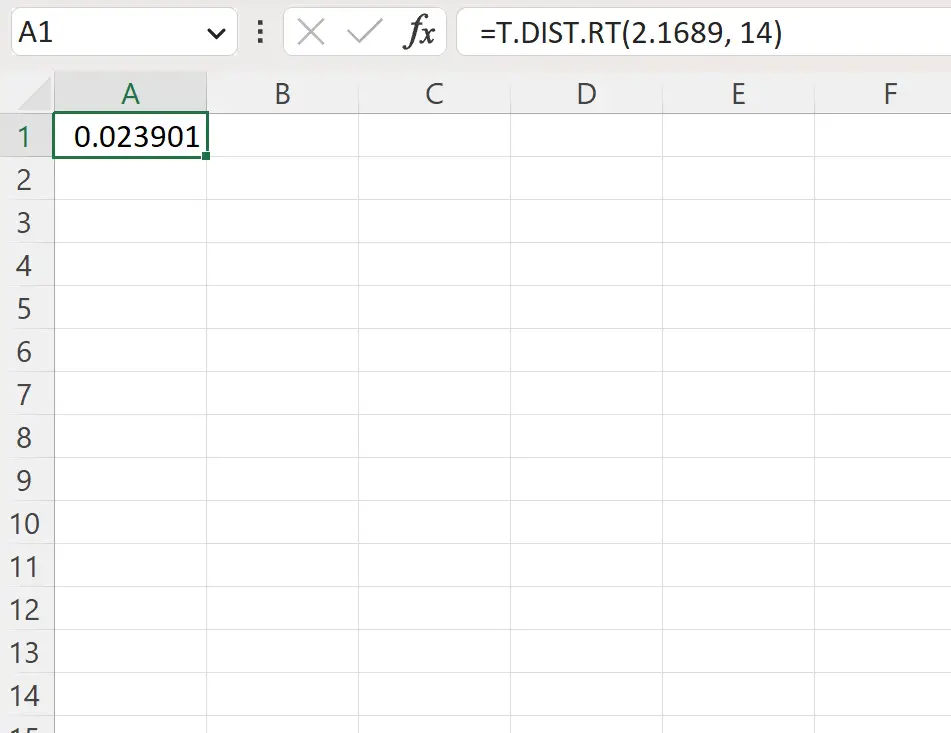
右侧的 p 值为0.023901 。

该值小于 0.05，植物学家可以拒绝原假设。她有足够的证据表明这种植物的真实平均高度超过 10 英寸。

其他资源

以下教程说明如何在 Excel 中执行其他常见任务：

如何在 Excel 中从 Z 分数查找 P 值
如何在 Excel 中查找 F 统计量的 P 值
如何在 Excel 中查找卡方统计量的 P 值