均值差的抽样分布
本文解释了统计学中两个均值之差的抽样分布是什么。您还将找到均值差的抽样分布公式,以及逐步解决的练习。
均值差的抽样分布是怎样的?
均值差异的抽样分布是通过计算两个不同总体的所有可能样本的均值之间的差异而得到的分布。
也就是说,为了获得均值差异的抽样分布,必须从两个研究总体中选择所有可能的样本,然后计算每个所选样本的均值,最后计算两个总体的所有均值之间的差。因此,应用所有这些操作后获得的值的集合形成了均值差的抽样分布。

均值抽样分布差用于计算从两个不同总体中随机选取的样本的两个均值之差接近总体均值之差的概率。
➤请参阅:均值的抽样分布
均值差的抽样分布公式
如果样本量足够大(n 1 ≥30且n 2 ≥30),均值差的抽样分布服从正态分布。更准确地说,所述分布的参数计算如下:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-90c67b74b4e9326b7869d641a59725d9_l3.png)
注意:如果两个总体都是正态分布,则无论样本大小如何,均值差的抽样分布都遵循正态分布。
因此,由于均值差的抽样分布是由正态分布定义的,因此均值差的抽样分布统计量的计算公式为:

金子:
-

是样本 i 的平均值。
-

是总体 i 的平均值。
-

是总体 i 的标准差。
-

是样本大小 i。
-

是由标准正态分布 N(0,1) 定义的变量。
请注意,来自不同人群的样本可能具有不同的样本量。
均值差的抽样分布的具体示例
一旦我们了解了均值抽样分布之差的定义及其公式是什么,我们将通过一个逐步的示例来完成对均值抽样分布之差的概念的理解。
- 在统计研究中,我们想要分析特定年龄的男孩和女孩的身高差异。我们知道,定义该年龄段男孩人口的分布的平均值为 157 厘米,标准差为 9 厘米,另一方面,定义该年龄段女孩人口的分布的平均值为 148 厘米厘米,标准差为 7 厘米。如果选取30个这个年龄段的男孩样本和35个这个年龄段的女孩样本,那么男孩样本的平均身高比女孩样本的平均身高大12厘米的概率是多少?
要解决这个问题,首先要做的是计算均值抽样分布之差的统计量。因此,我们应用上面的公式:
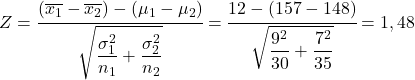
因此,男生平均样本身高比女生平均身高大12厘米的概率相当于Z变量大于1.48的概率。
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”253″ style=”vertical-align: -5px;”></p>
</p>
<p>因此,我们在<a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-683cd2a72980115d8d18c906d619370a_l3.png) Z 表中查找 Z>1.48 的概率:
Z 表中查找 Z>1.48 的概率:
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”331″ style=”vertical-align: -5px;”></p>
</p>
<p>简而言之,男生平均样本身高比女生平均身高大12厘米的概率为6.94%。</p>
</div><!-- End Content -->
<!-- Start Author Box -->
<div class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5b83fdc11bd2320249679c4752660451_l3.png)
关于作者
本杰明·安德森博
大家好,我是本杰明,一位退休的统计学教授,后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识,我渴望分享我的知识,通过 Statorials 增强学生的能力。了解更多